




2024年中考数学复习课件---微专题10 圆中常见辅助线的作法(含辅助圆)
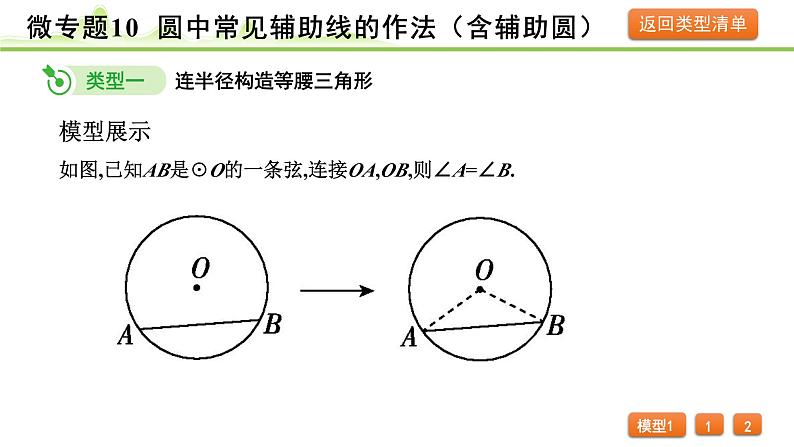
展开如图,已知AB是☉O的一条弦,连接OA,OB,则∠A=∠B.
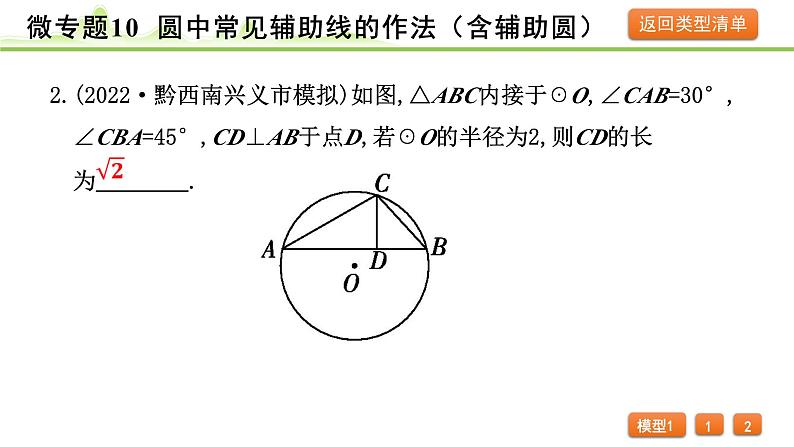
2.(2022·黔西南兴义市模拟)如图,△ABC内接于☉O,∠CAB=30°, ∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长 为 .
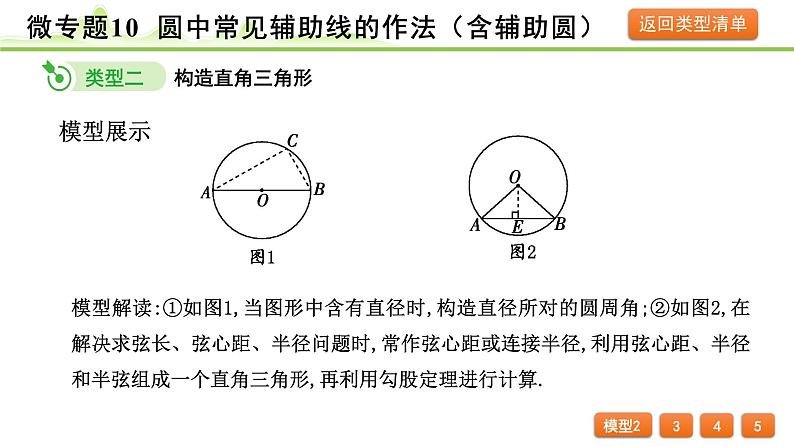
模型解读:①如图1,当图形中含有直径时,构造直径所对的圆周角;②如图2,在解决求弦长、弦心距、半径问题时,常作弦心距或连接半径,利用弦心距、半径和半弦组成一个直角三角形,再利用勾股定理进行计算.
5.(2022·铜仁三模)如图,两个同心圆,大圆的半径为5cm,小圆的半 径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范 是 .
8 cm
模型解读:固定的线段只要对应固定的角度,那么这个角的顶点轨迹为圆的一部分.
7.(2021·铜仁18题4分)如图,E,F分别是正 方形ABCD的边AB,BC上的动点,满 AE=BF,连接CE,DF,相交于点G,连接AG. 若正方形的边长为2,则线段AG的最小 为 .
已知平面内有一定点A和一动点B,若AB长度固定,则动点B的轨迹是以点A为圆心,AB长为半径的圆(如图)(依据:圆的定义,圆是平面内所有到定点的距离等于定长的点的集合).
9.(2017·黔东南州8题4分)如图,正方形ABCD中,E为AB中 点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( ) A.60° B.67.5° C.75° D.54°
10.(2022·毕节大方县二模)如图,在△ABC中,∠ACB=90°,点D是 AB的中点,将△ACD沿CD对折得△A'CD,连接BA',连接AA'交CD 于点E.若AB=14 cm,BA'=4 cm,则CE的长为( ) A.4 cm B.5 cm C.6 cm D.7 cm
11.(2022·遵义红花岗区一模)如图,在正方形ABCD内有一点P,AD=2, 点M是AB的中点,且∠PMA=2∠PAD.连接PD,则PD的最小值 为 .
如图1,图2所示,Rt△ABC和Rt△ABD共斜边,取AB的中点O,根据直角三角形斜边上的中线等于斜边的一半,可得OC=OD=OA=OB,故A,B,C,D四点共圆.
模型解读:共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆.
12.(2022·贵阳观山湖区模拟)如图,正方形ABCD的边长为2,E为射线 CD上一动点,以CE为边在正方形ABCD外作正方形CEFG,连接 BE,DG,两直线BE,DG相交于点P,连接AP,当线段AP的长为整数 时,AP的长为 .
中考数学复习方法技巧突破(七)圆中常见辅助线的作法教学课件: 这是一份中考数学复习方法技巧突破(七)圆中常见辅助线的作法教学课件,共10页。
中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件: 这是一份中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件,共9页。
中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件: 这是一份中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件,共10页。












