


2024年中考数学复习课件---微专题13 对称性质在求最值中的应用(精练册)
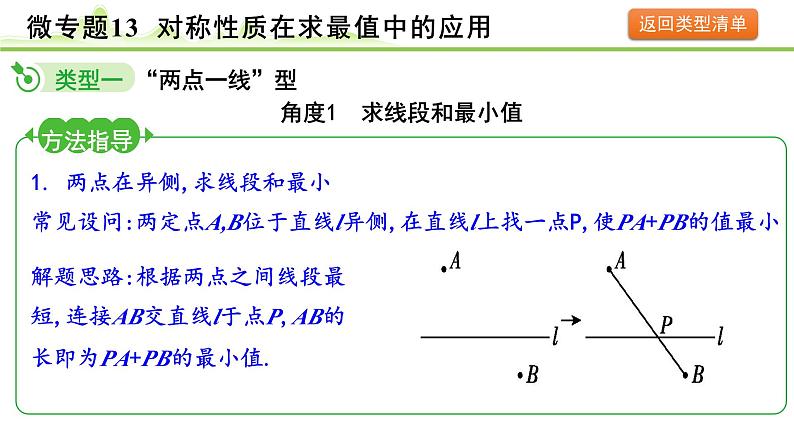
展开方法指导1. 两点在异侧,求线段和最小常见设问:两定点A,B位于直线l异侧,在直线l上找一点P,使PA+PB的值最小.
角度1 求线段和最小值
解题思路:根据两点之间线段最短,连接AB交直线l于点P,AB的长即为PA+PB的最小值.
方法指导2. 两点在同侧,求线段和最小常见设问:两定点A,B位于直线l同侧,在直线l上找一点P,使PA+PB的值最小.
解题思路:作点B关于直线l的对称点B',将同侧问题转化为异侧问题即可解决.
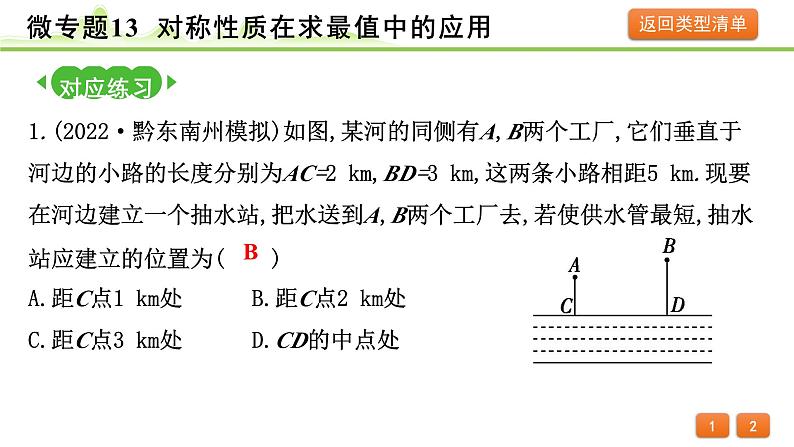
1.(2022·黔东南州模拟)如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2 km,BD=3 km,这两条小路相距5 km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )A.距C点1 km处 B.距C点2 km处C.距C点3 km处 D.CD的中点处
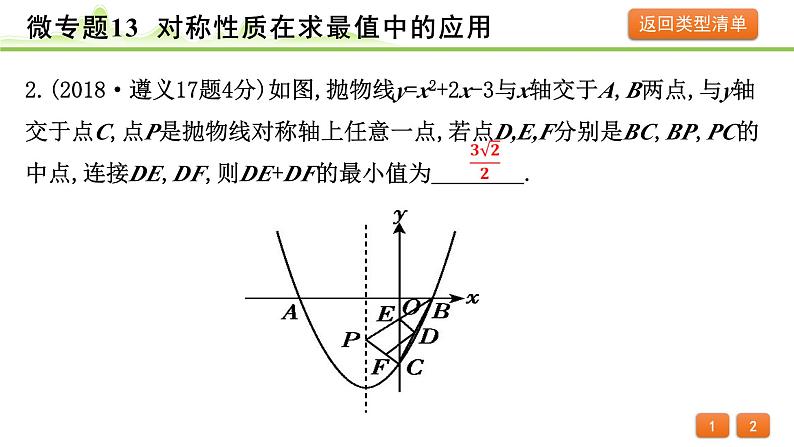
2.(2018·遵义17题4分)如图,抛物线y=x2+2x-3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D,E,F分别是BC,BP,PC的中点,连接DE,DF,则DE+DF的最小值为 .
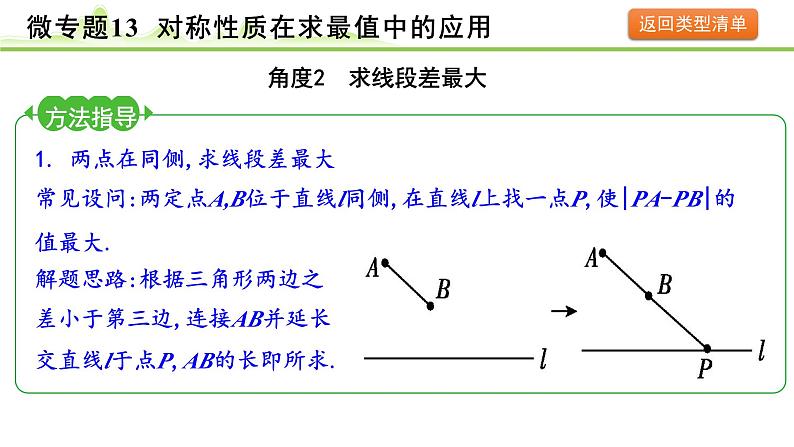
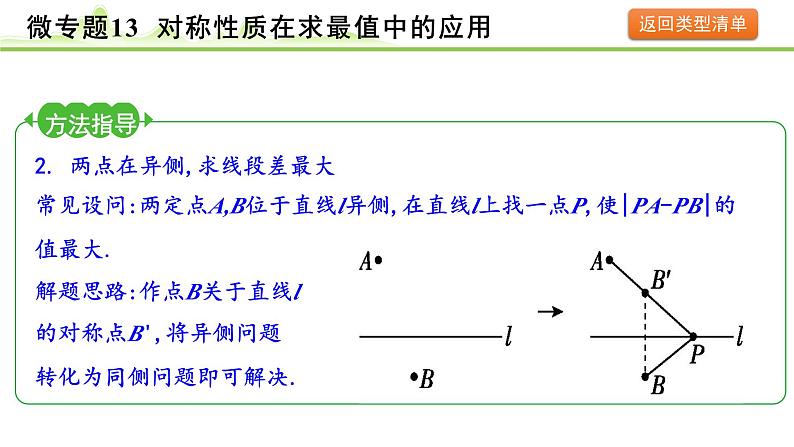
方法指导1. 两点在同侧,求线段差最大常见设问:两定点A,B位于直线l同侧,在直线l上找一点P,使|PA-PB|的值最大.
角度2 求线段差最大
解题思路:根据三角形两边之差小于第三边,连接AB并延长交直线l于点P,AB的长即所求.
方法指导2. 两点在异侧,求线段差最大常见设问:两定点A,B位于直线l异侧,在直线l上找一点P,使|PA-PB|的值最大.
解题思路:作点B关于直线l的对称点B',将异侧问题转化为同侧问题即可解决.
3.如图,在正方形ABCD中,AB=4,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=3,P为对角线BD上一点,则PM-PN的最大值为 .
解题思路:根据两点之间线段最短,分别作点P关于OA,OB的对称点并连接,三条线段转化到同一条线段上,P'P″的长即为△PCD周长的最小值.
方法指导1. 周长最小问题常见设问:点P在∠AOB内,在OA上找一点C,在OB上找一点D,使得△PCD的周长最小.
方法指导2. 线段和最小问题常见设问:点P是∠AOB内或边上一定点,在OA上找一点M,OB上找一点N,使得PN+MN的值最小.
解题思路:作点P关于OB的对称点P',再利用垂线段最短,过P'作OA的垂线,分别与OB,OA交于点N,M,P'M的长即为PN+MN的最小值.
4.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为 .
5.(2022·黔东南州二模)如图,在菱形ABCD中,AB=4,∠ABC=60°,点P,M分别是BD和BC上的动点,且点M与点B,C不重合,则PM+PC的最小值是 .
模型展示常见设问:点P,Q在∠AOB内,在OA上找一点M,在OB上找一点N,使得四边形PQNM的周长最小.
解题思路:PQ长为定值,四边形PQNM周长最小,即PM+MN+QN最小,利用“一点两线”型的思路解答即可.
6.如图,在∠MON的边OM,ON上分别有点A,D,且∠MON=30°,OA=10,OD=6,B,C两点分别是边OM,ON上的动点,则AC+BC+BD的最小值为 .
模型展示常见设问:已知l1∥l2,l1,l2之间距离为d,且在两定点A,B之间,在直线l1,l2上分别找点M,N点,使得MN⊥l1,且AM+MN+NB的值最小.
解题思路:将点A向下平移d个单位得到点A',根据两点之间线段最短,连接A'B交直线l2于点N,过点N作NM⊥l1于点M,则AM+MN+BN的值最小,最小值为A'B+MN.
2024年中考数学复习课件---微专题12 对称性质在折叠问题中的应用(精练册): 这是一份2024年中考数学复习课件---微专题12 对称性质在折叠问题中的应用(精练册),共15页。PPT课件主要包含了类型清单,方法指导等内容,欢迎下载使用。
中考数学复习微专题七代数最值问题模型二建立函数模型求最值课件: 这是一份中考数学复习微专题七代数最值问题模型二建立函数模型求最值课件,共9页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
中考数学复习微专题七代数最值问题模型一运用配方法求最值课件: 这是一份中考数学复习微专题七代数最值问题模型一运用配方法求最值课件,共6页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。












