07-专项素养综合全练(七)与三角形有关的角度问题2024年华东师大版数学七年级下册精品同步练习

这是一份07-专项素养综合全练(七)与三角形有关的角度问题2024年华东师大版数学七年级下册精品同步练习，共10页。

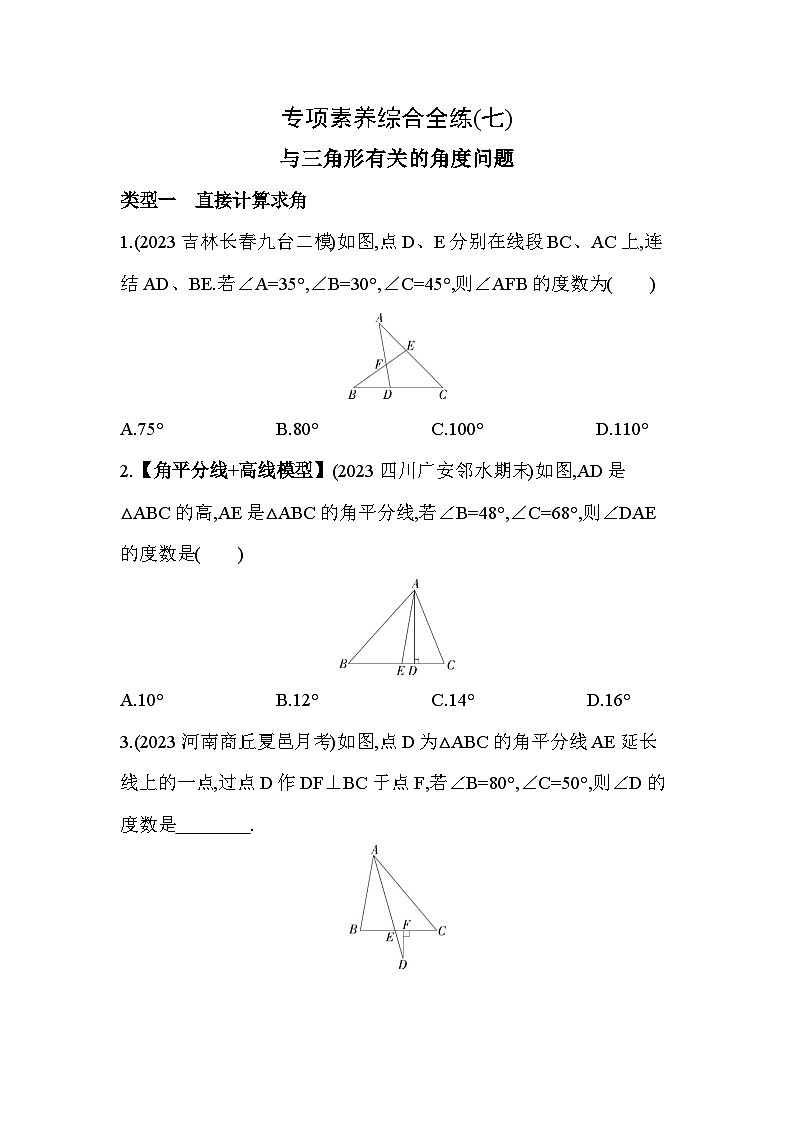
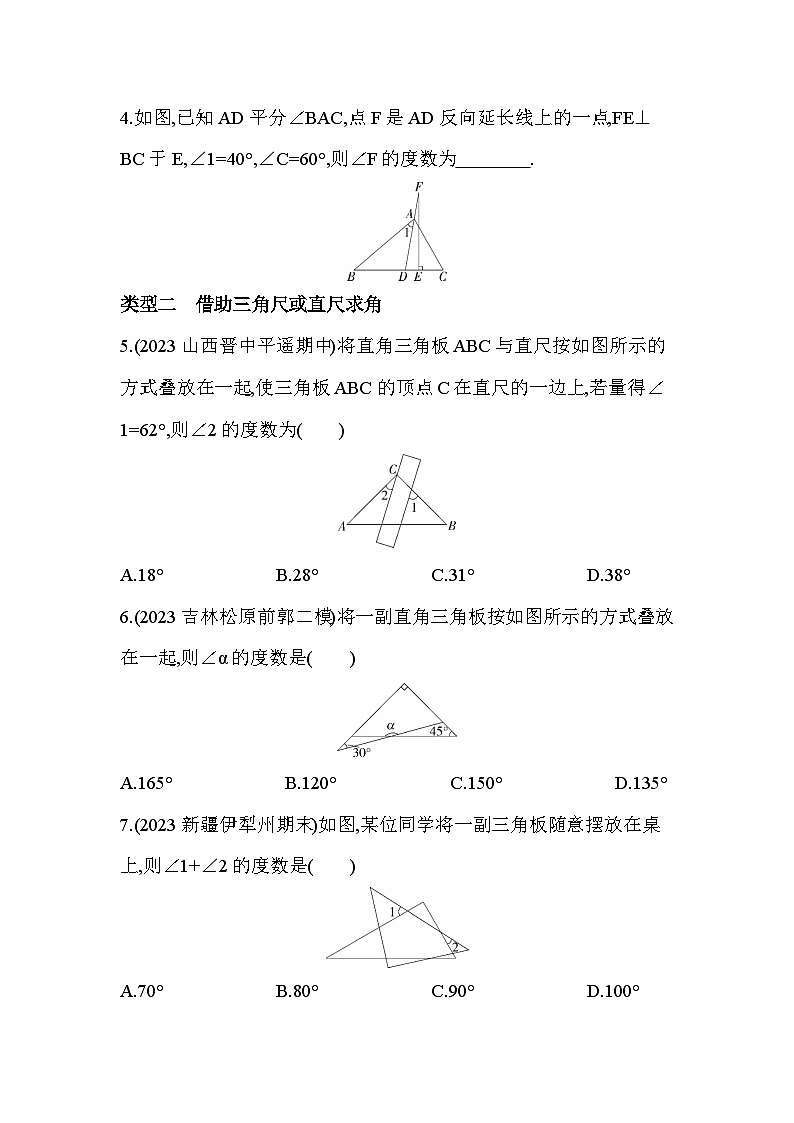
专项素养综合全练(七)与三角形有关的角度问题类型一　直接计算求角1.(2023吉林长春九台二模)如图,点D、E分别在线段BC、AC上,连结AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的度数为(　　)A.75°　　　　　　B.80°　　　　　　C.100°　　　　　　D.110°2.【角平分线+高线模型】(2023四川广安邻水期末)如图,AD是△ABC的高,AE是△ABC的角平分线,若∠B=48°,∠C=68°,则∠DAE的度数是(　　)A.10°　　　　　　B.12°　　　　　　C.14°　　　　　　D.16°3.(2023河南商丘夏邑月考)如图,点D为△ABC的角平分线AE延长线上的一点,过点D作DF⊥BC于点F,若∠B=80°,∠C=50°,则∠D的度数是　　　　. 4.如图,已知AD平分∠BAC,点F是AD反向延长线上的一点,FE⊥BC于E,∠1=40°,∠C=60°,则∠F的度数为　　　　. 类型二　借助三角尺或直尺求角5.(2023山西晋中平遥期中)将直角三角板ABC与直尺按如图所示的方式叠放在一起,使三角板ABC的顶点C在直尺的一边上,若量得∠1=62°,则∠2的度数为(　　)A.18°　　　　　　B.28°　　　　　　C.31°　　　　　　D.38°6.(2023吉林松原前郭二模)将一副直角三角板按如图所示的方式叠放在一起,则∠α的度数是(　　)A.165°　　　　　　B.120°　　　　　　C.150°　　　　　　D.135°7.(2023新疆伊犁州期末)如图,某位同学将一副三角板随意摆放在桌上,则∠1+∠2的度数是(　　)A.70°　　　　　　B.80°　　　　　　C.90°　　　　　　D.100°8.(2023吉林松原扶余二模)将一副三角板按如图所示的方式放置,使两条直角边重叠,则∠1的度数是(　　)A.30°　　　　　　B.45°　　　　　　C.50°　　　　　　D.75°9.(2022河南南阳唐河期末)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为　　　　. 类型三　与平行线的性质结合求角10.(2023吉林长春德惠二模)如图,AB∥CD,连结BC,点E是BC上一点,∠A=15°,∠C=27°,则∠AEC的度数为(　　)A.27°　　　　　　B.42°　　　　　　C.45°　　　　　　D.70°11.(2023河南濮阳南乐一模)如图,已知EF∥GH,Rt△ABC的两个顶点A,C分别在直线EF,GH上,∠B=90°,AB交GH于点D,若CD平分∠ACB,∠FAC=32°,则∠BAC的度数为(　　)A.20°　　　　　　B.24°　　　　　　C.26°　　　　　　D.33°12.(2023四川德阳旌阳一模)如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,过点F作FG∥CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=(　　)A.36°　　　　　　B.40°　　　　　　C.34°　　　　　　D.70°13.(2023河南商丘夏邑月考)如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠3=∠B,DE∥BC.(1)求证:∠1+∠2=180°;(2)若DE平分∠ADC,∠2=2∠B,求∠1的度数.类型四　应用折叠的性质求角14.(2022四川达州开江期末)如图,将△ABC沿着平行于BC的直线DE折叠,点A落在点A'处,若∠B=44°,则∠A'DB的度数是(　　)A.108°　　　　　　B.104°　　　　　　C.96°　　　　　　D.92°15.(2023江西赣州三中月考)如图,△ABC中,∠ACB=90°,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=22°,则∠DEA的度数为(　　)A.22°　　　　　　B.158°　　　　　　C.68°　　　　　　D.112°16.(2023福建三明宁化期中)如图,△ABC中,点M、N分别是AB、AC上的点,若将△ABC沿直线MN折叠,使点A落在AC边下方A'的位置,A'M与AC边交于点D,则∠1,∠2,∠A之间的数量关系是　　　　　　. 17.(2023河南南阳南召期末)如图1所示的三角形纸片ABC中,∠B=∠C,将纸片沿过点B的直线折叠,使点C落到AB边上的点E处,折痕为BD(如图2),再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图3),则∠ABC的度数为　　　　°. 图1　　图2　　图318.(2023四川成都简阳期末)如图,将三角形纸片ABC沿DE折叠,使点A落在点A'处,且BA'平分∠ABC,CA'平分∠ACB,若∠BA'C=110°,则∠1+∠2=　　　　. 答案全解全析D　∵∠A=35°,∠C=45°,∴∠FDB=∠A+C=35°+45°=80°,∵∠B=30°,∴∠AFB=∠B+∠FDB=30°+80°=110°,故选D.A　∵∠B=48°,∠C=68°,∴∠BAC=180°-∠B-∠C=64°,∵AE平分∠BAC,∴∠EAC=12∠BAC=32°,∵AD是BC边上的高,∴∠ADC=90°,∴∠DAC=90°-∠C=22°,∴∠DAE=∠EAC-∠DAC=32°-22°=10°,故选A.3.15°解析　∵∠B=80°,∠C=50°,∴∠BAC=180°-∠B-∠C=180°-80°-50°=50°,∵AD平分∠BAC,∴∠BAE=12∠BAC=25°,∴∠AEB=180°-∠B-∠BAE=75°,∴∠AEB=∠DEF=75°,∵DF⊥BC,∴∠DFE=90°,∴∠D=180°-∠DFE-∠DEF=180°-90°-75°=15°.解析　∵AD平分∠BAC,∠1=40°,∴∠BAC=2∠1=80°.∵∠C=60°,∴∠B=180°-∠BAC-∠C=180°-80°-60°=40°,∴∠EDF=∠B+∠1=40°+40°=80°.∵FE⊥BC,∴∠DEF=90°,∴∠F=90°-∠EDF=90°-80°=10°.B　如图,∵DE∥FG,∴∠1=∠3,∵∠ACB=90°,∴∠2+∠3=90°,∴∠1+∠2=90°,∵∠1=62°,∴∠2=90°-62°=28°,故选B.A　如图,由题意得∠A=30°,∠DCE=45°,∴∠ACD=135°,∴∠α=30°+135°=165°.故选A.C　如图,由题意得∠A=90°,∴∠ABC+∠ACB=180°-∠A=90°.∵∠ABC=∠1,∠ACB=∠2,∴∠1+∠2=∠ABC+∠ACB=90°.故选C.D　如图,∵∠AOC=90°-45°=45°,∴∠BOD=∠AOC=45°,∴∠1=∠BOD+∠B=45°+30°=75°.故选D.9.75°解析　如图,∵∠2+60°+45°=180°,∴∠2=75°,∵AB∥CD,∴∠1=∠2=75°.B　∵AB∥CD,∠C=27°,∴∠B=∠C=27°,∵∠A=15°,∴∠AEC=∠A+∠B=42°,故选B.C　∵EF∥GH,∠FAC=32°,∴∠ACD=∠FAC=32°,∵CD平分∠ACB,∴∠ACB=2∠ACD=2×32°=64°,∵∠B=90°,∴∠BAC=180°-90°-64°=26°.故选C.C　∵CE平分∠ACD,∠1=70°,∴∠FCE=∠1=70°,∴∠ACB=180°-70°×2=40°,∵FG∥CE,∴∠F=∠FCE=70°,∵∠2=36°,∴∠BAC=∠F+∠2=70°+36°=106°,∴∠3=180°-∠BAC-∠ACB=180°-106°-40°=34°,故选C.解析　(1)证明:∵DE∥BC,∴∠ADE=∠B,∵∠3=∠B,∴∠3=∠ADE,∴EF∥AB,∴∠2=∠DFE,∵∠1+∠DFE=180°,∴∠1+∠2=180°.∵DE平分∠ADC,∴∠ADC=2∠ADE,∵DE∥BC,∴∠ADE=∠B,∴∠ADC=2∠B,∵∠2=2∠B,∠2+∠ADC=180°,∴2∠B+2∠B=180°,解得∠B=45°,由(1)得AB∥EF,∴∠1=∠ADC=2∠B=90°.D　由题意得∠ADE=∠B=44°,∴∠A'DE=∠ADE=44°,∴∠A'DB=180°-44°-44°=92°,故选D.15.D　∵∠ACB=90°,∠A=22°,∴∠B=90°-∠A=68°,由折叠的性质可得∠CED=∠B=68°,∠DEA=180°-68°=112°,故选D.16.∠1=2∠A+∠2解析　由折叠的性质得∠A=∠A',∵∠1是△MDA的外角,∴∠1=∠A+∠MDA,同理可得∠MDA=∠2+∠A',∴∠1=∠A+∠2+∠A',即∠1=2∠A+∠2.17.72解析　设∠A=x,根据折叠的性质可知∠A=∠EDA=x,∠C=∠DEB=∠A+∠EDA=2x,∵AB=AC,∴∠ABC=∠C=2x,∵∠A+∠ABC+∠C=180°,∴5x=180°,解得x=36°,∴∠ABC=72°.18.80°解析　如图,连结AA'.∵∠BA'C=110°,∴∠A'BC+∠A'CB=70°,∵BA'平分∠ABC,CA'平分∠ACB,∴∠ABC+∠ACB=140°,∴∠BAC=180°-140°=40°,由折叠的性质得∠DA'E=∠DAE=40°.∵∠1=∠DAA'+∠DA'A,∠2=∠EAA'+∠EA'A,∴∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠DAE+∠DA'E=80°.