05-专项素养综合全练（五）数形结合——整式乘法与几何图形相结合--2024年冀教版数学七年级下册精品同步练习

这是一份05-专项素养综合全练（五）数形结合——整式乘法与几何图形相结合--2024年冀教版数学七年级下册精品同步练习，共5页。

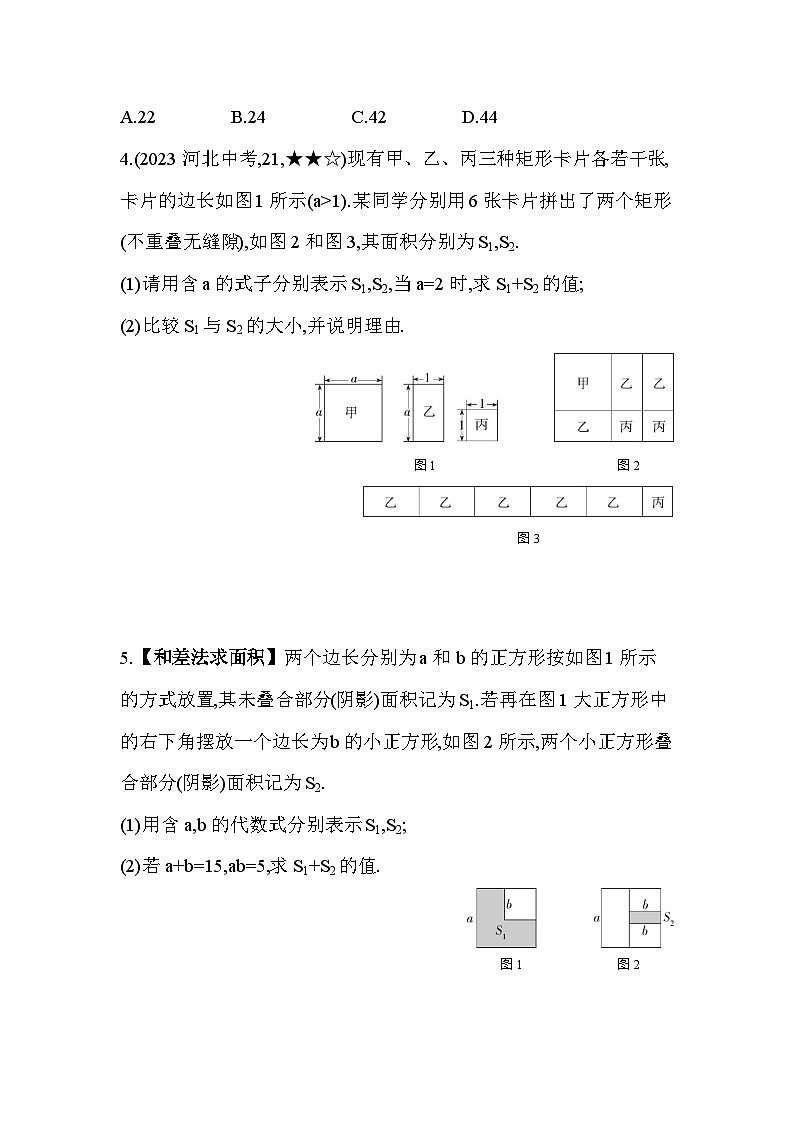
专项素养综合全练(五)数形结合——整式乘法与几何图形相结合类型一　以形助数,验证乘法公式1.(2023江苏启东期末)能够用图中已有图形的面积说明的等式是(　　)A.a(a+4)=a2+4a　　　 　B.(a+4)(a-4)=a2-16C.(a+2)2=a2+4a+4　　　　D.(a+2)(a-2)=a2-4 第1题图 第2题图2.你能根据图中阴影部分的面积关系得到的数学公式是(　　)A.a(a-b)=a2-ab　　　 　B.(a+b)2=a2+2ab+b2C.(a-b)2=a2-2ab+b2　　　　D.a(a+b)=a2+ab类型二　用数解形,图形周长或面积的计算3.【和差法求面积】如图,有两张正方形纸片A和B,图1中将B放置在A内部,测得阴影部分面积为2.图2中将正方形纸片A、B并列放置后构造新正方形,测得阴影部分面积为20.若将3个正方形纸片A和2个正方形纸片B并列放置后构造新正方形如图3(图2,图3中正方形纸片A、B均无重叠),则图3中阴影部分的面积为(　　)　 　 　图1 图2 图3A.22　　　　B.24 C.42　　　　D.444.(2023河北中考,21,★★☆)现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图1所示(a>1).某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为S1,S2.(1)请用含a的式子分别表示S1,S2,当a=2时,求S1+S2的值;(2)比较S1与S2的大小,并说明理由. 　 图1 图2 图3 5.【和差法求面积】两个边长分别为a和b的正方形按如图1所示的方式放置,其未叠合部分(阴影)面积记为S1.若再在图1大正方形中的右下角摆放一个边长为b的小正方形,如图2所示,两个小正方形叠合部分(阴影)面积记为S2.(1)用含a,b的代数式分别表示S1,S2;(2)若a+b=15,ab=5,求S1+S2的值. 　图1 图2 答案全解全析1.D　如图,长方形③与长方形②的面积相等,正方形④的面积为2×2=4,于是有S①+S②=(a+2)(a-2)=S①+S③=(S①+S③+S④)-S④=a2-4,所以(a+2)(a-2)=a2-4,故选D.2.C　题图中大阴影正方形的边长为a-b,所以大阴影正方形的面积为(a-b)2.大阴影正方形面积也等于边长为a的正方形的面积减去边长为b的小正方形的面积,再减去两个长为a-b,宽为b的长方形的面积,即a2-b2-2(a-b)b=a2+b2-2ab,所以有(a-b)2=a2-2ab+b2,故选C.3.C　设正方形纸片A的边长为a,正方形纸片B的边长为b.题图1中阴影部分的面积=a2-b2=2.题图2中阴影部分的面积=(a+b)2-a2-b2=20,所以ab=10.题图3中阴影部分的面积=(2a+b)2-3a2-2b2=4a2+4ab+b2-3a2-2b2=a2-b2+4ab=2+40=42.故选C.方法解读　和差法求面积就是把所求图形的面积转化为若干个图形面积的和或差来计算.4.解析　(1)由题图可知S1=(a+2)(a+1)=a2+a+2a+2=a2+3a+2,S2=(5a+1)×1=5a+1,当a=2时,S1+S2=4+6+2+10+1=23.(2)S1>S2.理由:∵S1-S2=a2+3a+2-5a-1=a2-2a+1=(a-1)2,∵a>1,∴(a-1)2>0,∴S1>S2.5.解析　(1)题图1中阴影部分的面积等于边长为a的正方形与边长为b的正方形的面积差,所以S1=a2-b2.题图2中阴影部分的面积为两个边长为b的正方形的面积和减去长为a,宽为b的长方形的面积,所以S2=2b2-ab.(2)∵a+b=15,ab=5,∴S1+S2=(a2-b2)+(2b2-ab)=a2+b2-ab=(a+b)2-3ab=152-3×5=225-15=210.∴S1+S2的值为210.