2024高考数学二轮复习压轴题型分类专练（新高考用）-专题04空间向量与立体几何（含解析）

这是一份2024高考数学二轮复习压轴题型分类专练（新高考用）-专题04空间向量与立体几何（含解析），共33页。
（2023•新高考Ⅰ）如图，在正四棱柱中，，．点，，，分别在棱，，，上，，，．
证明：；
点在棱上，当二面角为时，求．
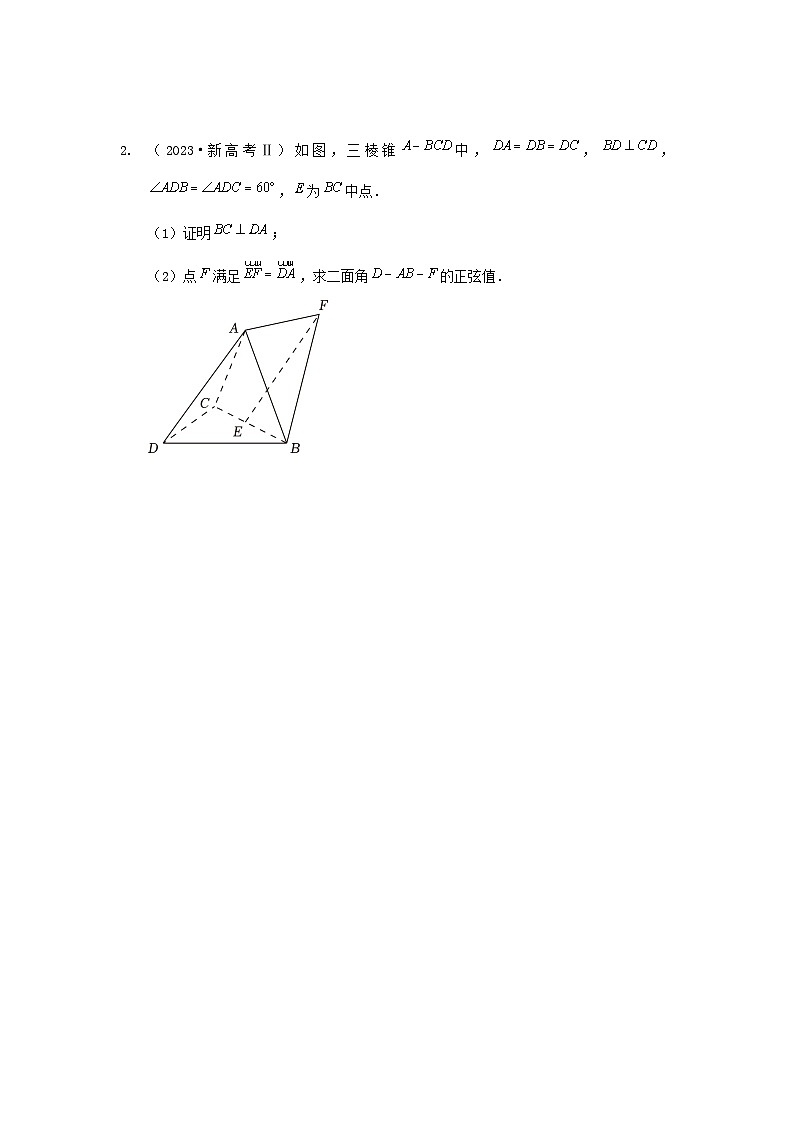
（2023•新高考Ⅱ）如图，三棱锥中，，，，为中点．
（1）证明；
（2）点满足，求二面角的正弦值．
（2022•新高考Ⅰ）如图，直三棱柱的体积为4，△的面积为．
（1）求到平面的距离；
（2）设为的中点，，平面平面，求二面角的正弦值．
（2022•新高考Ⅱ）如图，是三棱锥的高，，，为的中点．
（1）证明：平面；
（2）若，，，求二面角的正弦值．
（2023•上海·统考高考真题）已知直四棱柱，，，，，．
（1）证明：直线平面；
（2）若该四棱柱的体积为36，求二面角的大小．
（2023•河北保定•区联考二模）如图，四棱台ABCD﹣EFGH的底面是菱形，且∠BAD＝，DH⊥平面ABCD，EH＝2，DH＝3，AD＝4．
（1）求证：AE∥平面BDG；
（2）求三棱锥 F﹣BDG的体积．
（2023•新疆乌鲁木齐·统考模拟）在△ABC中，∠ACB＝45°，BC＝3，过点A作AD⊥BC，交线段BC于点D（如图1），沿AD将△ABD折起，使∠BDC＝90°（如图2）点E，M分别为棱BC，AC的中点．
（1）求证：CD⊥ME；
（2）求三棱锥A﹣BCD的体积最大值．
（2023•广东广州·校级模拟）图①是直角梯形ABCD，AB∥CD，∠D＝90°，四边形ABCE是边长为2的菱形，并且∠BCE＝60°，以BE为折痕将△BCE折起，使点C到达C1的位置，且AC1＝．
（1）求证：平面BC1E⊥平面ABED；
（2）在棱DC1上是否存在点P，使得点P到平面ABC1的距离为？若存在，求出直线EP与平面ABC1所成角的正弦值；若不存在，请说明理由．
（2023•浙江温州·统考模拟）如图，在四棱锥P﹣ABCD中，AB∥CD，∠ABC＝90°，△ADP是等边三角形，AB＝AP＝2，BP＝3，AD⊥BP．
（Ⅰ）求BC的长度；
（Ⅱ）求直线BC与平面ADP所成的角的正弦值．
（2023•上海奉贤•二模）如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP＝∠CDP＝90°．
（1）证明：平面PAB⊥平面PAD；
（2）若PA＝PD＝AB＝DC，∠APD＝90°，且四棱锥P﹣ABCD的体积为，
求PB与平面ABCD所成的线面角的大小．
（2023·江苏徐州·统考模拟）如图，在四棱锥P﹣ABCD中，侧棱PA⊥平面ABCD，底面四边形ABCD是矩形，PA＝AD＝4，点M，N分别为棱PB，PD的中点，点E在棱AD上，AD＝3AE．
（1）求证：直线AM∥平面BNE；
（2）从下面①②两个条件中选取一个作为已知，证明另外一个成立．
①平面PAB与平面PCD的交线l与直线BE所成角的余弦值为；
②二面角N﹣BE﹣D的余弦值为．
注：若选择不同的组合分别作答，则按第一个解答计分．
（2023·江西·模拟预测）如图所示，圆锥的高，底面圆O的半径为1，延长直径AB到点C，使得BC＝1，分别过点A，C作底面圆O的切线，两切线相交于点E，点D是切线CE与圆O的切点．
（1）证明：平面PDE⊥平面POD；
（2）点E到平面PAD的距离为d1，求d1的值．
（2023·山东枣庄·校级模拟）在直角梯形AA1B1B中，A1B1∥AB，AA1⊥AB，AB＝AA1＝2A1B1＝6，直角梯形AA1B1B绕直角边AA1旋转一周得到如下图的圆台A1A，已知点P，Q分别在线段CC1，BC上，二面角B1﹣AA1﹣C1的大小为θ．
（1）若θ＝120°，，AQ⊥AB，证明：PQ∥平面AA1B1B；
（2）若θ＝90°，点P为CC1上的动点，点Q为BC的中点，求PQ与平面AA1C1C所成最大角的正切值，并求此时二面角Q﹣AP﹣C的余弦值．
（2023·黑龙江哈尔滨·校级四模）如图1，在等腰梯形ABCD中，AD∥BC，AD＝4，BC＝2，∠DAB＝60°，点E，F在以AD为直径的半圆上，且＝＝，将半圆沿AD翻折如图2．
（1）求证：EF∥平面ABCD；
（2）当多面体ABE﹣DCF的体积为4时，求平面ABE与平面CDF夹角的余弦值．
（2022·浙江·统考高考真题）如图，已知和都是直角梯形，，，，，，，二面角的平面角为．设，分别为，的中点．
（Ⅰ）证明：；
（Ⅱ）求直线与平面所成角的正弦值．
题型训练
答案&解析
【1】
【解析】（1）证明：根据题意建系如图，则有：
，2，，，0，，，2，，，0，，
，，
，又，，，四点不共线，
；
（2）在（1）的坐标系下，可设，2，，，，
又由（1）知，0，，，2，，，0，，
，，，
设平面的法向量为，
则，取，
设平面的法向量为，
则，取，
根据题意可得，，
，
，又，，
解得或，
为的中点或的中点，
．
【2】
【解析】证明：（1）连接，，
，为中点．
，
又，，
与 均为等边三角形，
，
，，
平面，
平面，
．
（2）解：设，
，
，，
，
，
又，，
平面，
以为原点，建立如图所示空间直角坐标系，
，，，，0，，
，
，
，，，
设平面与平面的一个法向量分别为，，
则，令，解得，
，令，解得，，
故，1，，，1，，
设二面角的平面角为，
则，
故，
所以二面角的正弦值为．
【3】
【解析】（1）由直三棱柱的体积为4，可得，
设到平面的距离为，由，
，，解得．
（2）连接交于点，，四边形为正方形，
，又平面平面，平面平面，
平面，，
由直三棱柱知平面，，又，
平面，，
以为坐标原点，，，所在直线为坐标轴建立如图所示的空间直角坐标系，
，，又，解得，
则，0，，，2，，，0，，，2，，，1，，
则，2，，，1，，，0，，
设平面的一个法向量为，，，
则，令，则，，
平面的一个法向量为，0，，
设平面的一个法向量为，，，
，令，则，，
平面的一个法向量为，1，，
，，
二面角的正弦值为．
【4】
【解析】（1）证明：连接，，依题意，平面，
又平面，平面，则，，
，
又，，则，
，
延长交于点，又，则在中，为中点，连接，
在中，，分别为，的中点，则，
平面，平面，
平面；
（2）过点作，以，，分别为轴，轴，轴建立如图所示的空间直角坐标系，
由于，，由（1）知，
又，则，
，
又，即，12，，
设平面的一个法向量为，又，
则，则可取，
设平面的一个法向量为，又，
则，则可取，
设锐二面角的平面角为，则，
，即二面角正弦值为．
【5】
【解析】（1）证明：根据题意可知，，且，
可得平面平面，又直线平面，
直线平面；
（2）设，则根据题意可得该四棱柱的体积为，
，底面，在底面内过作，垂足点为，
则在底面内的射影为，
根据三垂线定理可得，
故即为所求，
在中，，，，
，又，
，
二面角的大小为．
【6】
【解答】解：（1）证明：如图，连接AC交BD于点O，连接EG，GO，
由ABCD﹣EFGH为四棱台，可知ACGE四点共面，且EG⊂面EFGH，AC⊂面ABCD，
∴EG∥AC，
∵EFGH和ABCD均为菱形，且，EH＝2，AD＝4，
∴，
∴四边形AOGE为平行四边形，
∴AE∥GO，
又GO⊂面BDG，AE⊄面BDG，
∴AE∥平面BDG；
（2）连接GE交FH于K，
∵GE⊥FH，FD⊥GE，FH∩DH＝D，FH⊂面BDHF，DH⊂面BDHF，
∴GE⊥面BDHF，
∵四边形ABCD为菱形且，EF＝2，
∴，
∴．
【7】
【解答】解：（1）在△ABC中，M，E分别为AC，BC的中点，则ME∥AB，
折叠前AD⊥BC则折叠后AD⊥CD，又∠BDC＝90°即CD⊥BD，且AD⋂BD＝D，
又AD⊂平面ADB，BD⊂平面ADB，所以CD⊥平面ADB，
又AB⊂平面ADB，所以CD⊥AB，而ME∥AB，所以CD⊥ME；
（2）设BD＝x（0＜x＜3），则CD＝3﹣x，
因为AD⊥CD，AD⊥BD，且CD⋂BD＝D，
又CD⊂平面BDC，BD⊂平面BDC，所以AD⊥平面BDC，
所以AD为三棱锥A﹣BCD的高，
在△ADC中，∠ACD＝45°，∠ADC＝90°，所以AD＝CD＝3﹣x，
所以，
则，令V′＝0解得x＝1或x＝3（舍去），
令V′＞0解得0＜x＜1，令V′＜0解得1＜x＜3，
所以在（0，1）上单调递增，在（1，3）上单调递减，
故当x＝1即当BD＝1，CD＝2时，VA﹣BCD取最大值，
此时．
【8】
【解答】解：（1）证明：如图所示，
在图①中，连接AC，交BE于O，因为四边形ABCE是边长为2的菱形，且∠BCE＝60°，
所以AC⊥BE，且，
在图②中，相交直线OA，OC1均与BE垂直，
所以∠AOC1是二面角A﹣BE﹣C1的平面角，
因为，
所以，
所以OA⊥OC1，
所以平面BC1E⊥平面ABED．
（2）由（1）知，分别以直线OA，OB，OC1为x，y，z轴建立如图②所示的空间直角坐标系，
则，，，B（0，1，0），E（0，﹣1，0），
所以，，，，，
设，λ∈[0，1]，
则，
设平面ABC1的一个法向量，
则，
令x＝1，则y＝，z＝1，
所以．
因为P到平面ABC1的距离为，
所以，
解得，
由，得（xP﹣，yP+，zP）＝（﹣，，），
所以xP＝，yP＝﹣，zP＝，
所以，
所以．
设直线EP与平面ABC1所成的角为θ，
所以．
【9】
【解答】解：（I）取AD中点F，连PF、BF，
∵△ADP是等边三角形，∴PF⊥AD，……………………（2分）
又∵AD⊥BP，
∴AD⊥平面PFB，∵BF⊂平面PFB，∴AD⊥BF，………………………（4分）
∴BD＝AB＝2，∴BC＝． …………………………（6分）
（II）∵AD⊥平面PFB，AD⊂平面APD
∴平面PFB⊥平面APD …………………………………（8分）
作BG⊥PF交PF为G，则BG⊥平面APD，AD、BC交于H，
∠BHG为直线BC与平面ADP所成的角，…………（10分）
由题意得PF＝BF＝，又∵BP＝3，
∴∠GFB＝30°，BG＝，……………………（12分）
∵∠ABC＝∠BCD＝90°，∴CD＝1，∴BH＝2，
∴sin∠BHG＝．
∴直线BC与平面ADP所成的角的正弦值为．……………………（15分）
【10】
【解答】证明：（1）∵在四棱锥P﹣ABCD中，∠BAP＝∠CDP＝90°，
∴AB⊥PA，CD⊥PD，
又∵AB∥CD，
∴AB⊥PD，
∵PA∩PD＝P，
∴AB⊥平面PAD，
∵AB⊂平面PAB，
∴平面PAB⊥平面PAD；
（2）解：取AD中点O，连结PO，
∵PA＝PD，O为AD的中点，
∴PO⊥AD，
∴AB⊥平面PAD，AD⊂平面PAD，
∴AB⊥PO，
∵AB∩AD＝A，
∴PO⊥底面ABCD，
设PA＝PD＝AB＝DC＝a，
则，，
∵四棱锥P﹣ABCD的体积为，PO⊥底面ABCD，
∴＝，解得a＝2，
＝，
∴，
∵PO⊥底面ABCD，
∴∠PBO为PB与平面ABCD所成的角，
在Rt△POB中，，
∴∠PBO＝30°，
故PB与平面ABCD所成的线面角为30°．
【11】
【解答】解：（1）证明：如图，连接MD，交BN于点F，连接EF，
因为M，N分别为棱PB，PD的中点，
所以F为△PBD的重心，则MD＝3MF，
又在△AMD中，AD＝3AE，
所以EF∥AM，
又因为EF⊂平面BNE，AM⊄平面BNE，
所以AM∥平面BNE．
（2）若选①作为已知条件：
在矩形ABCD中，AB∥CD，CD⊂平面PCD，
AB⊄平面PCD，所以AB∥平面PCD．
又AB⊂平面PAB，平面PAB∩平面PCD＝l，
所以AB∥l．
所以l与直线BE所成角即为∠ABE．
在直角三角形ABE中，，AB⊥AE，
所以由可得，AB＝4
建立如图所示的空间直角坐标系，
则B（4，0，0），，N（0，2，2），
所以，．
设平面BNE的法向量为，
则，可得，则可取．
又为平面BDE的一个法向量，
所以．
由图可知，二面角N﹣BE﹣D的余弦值为．
若选②为已知条件：
建立如图所示的空间直角坐标系，
因为，设AB＝m，则B（m，0，0），，N（0，2，2），
则，．
设平面BNE的法向量为，
则，即，则可取．
又为平面BDE的一个法向量，且二面角N﹣BE﹣D的余弦值为，
所以，解得m＝4．
在矩形ABCD中，AB∥CD，CD⊂平面PCD，AB⊄平面PCD，
所以AB∥平面PCD．
又AB⊂平面PAB，平面PAB∩平面PCD＝l，
所以AB∥l．
所以l与直线BE所成角即为∠ABE．
在直角三角形ABE中，AB⊥AE，AB＝4，，可得，
所以平面PAB与平面PCD的交线l与直线BE所成角的余弦值为．
【12】
【解答】解：（1）证明：由题设，PO⊥平面ABD，又D是切线CE与圆O的切点，
所以CE⊂平面ABD，则PO⊥CE，且OD⊥CE，
又PO∩OD＝O，PO，OD⊂平面POD，
所以CE⊥平面POD，
又CE⊂平面PDE，
所以平面PDE⊥平面POD．
（2）因为OD⊥CE，OD＝1，OC＝2，
所以，∠OCD＝30°，
又AE⊥AC，CA＝3，
所以，
所以，
所以，且△ADE的面积为，
因为，
所以PA＝PD＝2，
所以△PAD为等腰三角形，其底边AD上的高为，
所以△PAD的面积为，
因为，
所以，
所以．
【13】
【解答】（1）证明：∵AA1⊥AB，∴AA1⊥AC，∴∠BAC＝∠B1A1C1＝θ＝120°，
又AB∩AC＝A，AB，AC⊂平面ABC，∴AA1⊥平面ABC，
又AQ⊂平面ABC，∴AA1⊥AQ，又AQ⊥AB，
如图，以A为原点，AB，AQ，AA1所在直线分别为x，y，z轴建立空间直角坐标系，
由于AB＝AA1＝2A1B1＝6，∴，
则，
又，∴，则，
∴，又y轴⊥平面AA1B1B，
故可为平面AA1B1B的一个法向量，
又，且PQ⊄平面AA1B1B，∴PQ∥平面AA1B1B；
（2）解：∵AA1⊥AB，∴AA1⊥AC，∴∠BAC＝∠B1A1C1＝θ＝90°，
如图，以A为原点，AB，AC，AA1所在直线分别为x，y，z轴建立空间直角坐标系，
则B（6，0，0），C（0，6，0），C1（0，3，6），Q（3，3，0），
设，则，
则，
又x轴⊥平面AA1C1C，∴可作为平面AA1C1C的一个法向量，
设PQ与平面AA1C1C所成角为α，且，
则，
又函数y＝sinα与y＝tanα均在上单调递增，
∴当时，有最大值为，此时tanα也取到最大值，
又，则；
设为平面APQ的法向量，又，
∴，令z＝9，则平面APQ的法向量，
平面APC的一个法向量为，
∴，由图可知二面角Q﹣AP﹣C为锐角，即二面角Q﹣AP﹣C的余弦值为．
∴PQ与平面AA1C1C所成最大角的正切值为，此时二面角Q﹣AP﹣C的余弦值为．
【14】
【解答】（1）证明：连接AE，EF，FD，六边形ABCDFE为正六边形，则EF∥AD∥BC，
在翻折过程中，EF∥AD，EF⊄平面ABCD，AD⊂平面ABCD，所以EF∥平面ABCD．
（2）解：连接EB，FC分别交AD于G，H，则EB⊥AD，FC⊥AD，
翻折过程中，EG⊂平面EGB，GB⊂平面EGB，EG∩GB＝G，
AD⊥EG，AD⊥GB，所以AD⊥平面EGB，同理AD⊥平面FHC，
所以平面EGB∥平面FHC．又因为EF∥GH∥BC，
则三棱柱EGB﹣FHC为直三棱柱，EG∥FH，BG∥HC，
且EG＝GB＝FH＝HC＝，AG＝HD＝1，GH＝2．
设∠EGB＝θ，所以，
V＝V三棱锥A﹣EGB+V三棱柱EGB﹣FHC+V三棱锥D﹣FHC＝AG•S△EGB+GH•S△EGB+HD•S△FHC＝4sinθ＝4．
所以sinθ＝1，即，AD⊥EG，AD⊥GB，∠EGB为二面角E﹣AD﹣B的平面角，
即平面EFDA⊥平面ABCD．以G为坐标原点，GB，GD，GE所在的直线为x，y，z轴，
建立空间直角坐标系如图，则A（0，﹣1，0），，，
，2，0），D（0，3，0），F（0，2，），
，
设平面ABE的一个法向量，有，
令x＝1得，同理可得平面CDF的法向量，
设平面ABE与平面CDF的夹角为φ，观察图可知其为锐角，则csφ＝＝，
所以平面ABE与平面CDF的夹角的余弦值为．
【15】
【解析】证明：由于，，
平面平面，平面，平面，
所以为二面角的平面角，
则，平面，则．
又，
则是等边三角形，则，
因为，，，平面，平面，
所以平面，因为平面，所以，
又因为，平面，平面，
所以平面，因为平面，故；
解：（Ⅱ）由于平面，如图建系：
于是，则，
，
设平面的法向量，，，
则，，令，则，，
平面的法向量，
设与平面所成角为，
则．