数学19.2 平行四边形作业ppt课件

这是一份数学19.2 平行四边形作业ppt课件，共39页。PPT课件主要包含了答案呈现，习题链接，点方法，2BE∥DF等内容，欢迎下载使用。
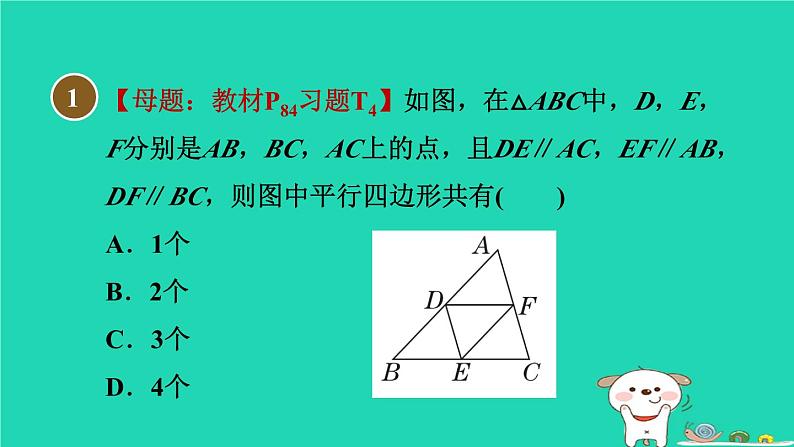
【母题：教材P84习题T4】如图，在△ABC中，D，E，F分别是AB，BC，AC上的点，且DE∥AC，EF∥AB，DF∥BC，则图中平行四边形共有(　　)A．1个 B．2个 C．3个 D．4个
∵DE∥AC，EF∥AB，DF∥BC，∴图中的平行四边形有▱ADEF，▱BEFD，▱DECF.
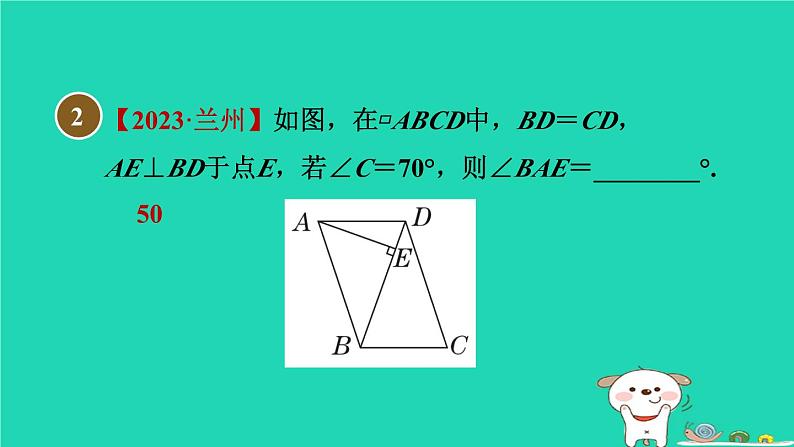
【2023·兰州】如图，在▱ABCD中，BD＝CD，AE⊥BD于点E，若∠C＝70°，则∠BAE＝________°.
在△DBC中，∵BD＝CD，∠C＝70°，∴∠DBC＝∠C＝70°.∵四边形ABCD为平行四边形，∴AD∥BC，∠BAD＝∠C＝70°，∴∠ADB＝∠DBC＝70°.又∵AE⊥BD，∴∠DAE＝90°－∠ADB＝90°－70°＝20°.∴∠BAE＝∠BAD－∠DAE＝50°.
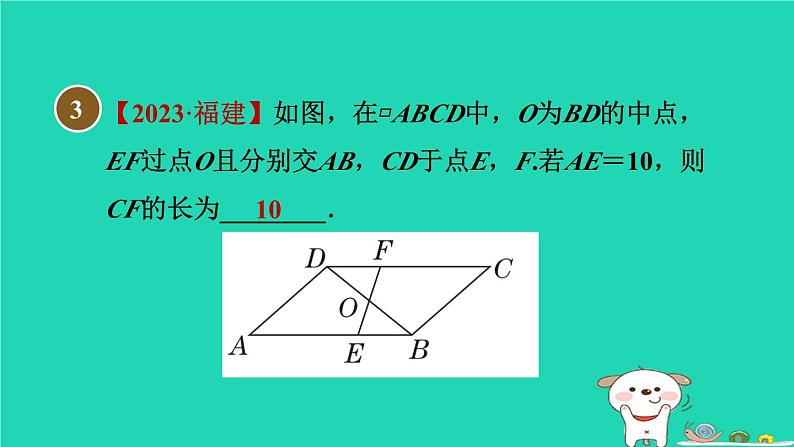
【2023·福建】如图，在▱ABCD中，O为BD的中点，EF过点O且分别交AB，CD于点E，F.若AE＝10，则CF的长为________．
∵四边形ABCD是平行四边形，∴CD＝AB，CD∥AB.∴∠FDO＝∠EBO，∠DFO＝∠BEO.∵O为BD的中点，∴OD＝OB.∴△DOF≌△BOE(AAS)．∴DF＝BE.∴CD－DF＝AB－BE.∴CF＝AE＝10.
【2023·聊城】如图，在▱ABCD中，BC的垂直平分线EO交AD于点E，交BC于点O，连接BE，CE，过点C作CF∥BE，交EO的延长线于点F，连接BF.若AD＝8，CE＝5，则四边形BFCE的面积为________．
【母题：教材P76例1】如图，在▱ABCD中，AE平分∠BAD且交BC于点E，∠D＝58°，则∠AEC的大小是(　　)A．61° B．109° C．119° D．122°
【母题：教材P84习题T2】如图，已知直线a∥b，点A，B，C在直线a上，点D，E，F在直线b上，AB＝EF，若△CEF的面积为5，则△ABD的面积为(　　)A．2 B．4 C．5 D．10
如图，已知l1∥l2，AB∥CD，AD＝CE，DE，FG都垂直于l2，垂足分别为E，G，则下列选项中，一定成立的是(　　)A．AB＝CD　　　B．CE＝FGC．BC＝EG　　　D．S四边形ABCD＞S四边形DEGF
在▱ABCD中，∠DAB的平分线分边BC为3 cm和 4 cm两部分，则▱ABCD的周长为(　　)A．20 cm B．22 cmC．10 cm D．20 cm或22 cm
如图①，当BE＝3 cm时，CE＝4 cm.∵四边形ABCD为平行四边形，∴AD∥BC.∴∠DAE＝∠AEB.∵AE平分∠BAD，∴∠BAE＝∠DAE.∴∠BAE＝∠AEB.∴AB＝BE＝3 cm.∴▱ABCD的周长为(3＋3＋4)×2＝20(cm)．
如图②，当BE＝4 cm时，CE＝3 cm.同理可得AB＝BE＝4 cm，∴▱ABCD的周长为(4＋4＋3)×2＝22(cm)．
本题利用了分类讨论思想，AE把BC分成3 cm和4 cm两部分，没有明确哪部分是3 cm，哪部分是4 cm，故分两种情况．
【2023·南充】如图，在▱ABCD中，点E，F在对角线AC上，∠CBE＝∠ADF.求证：(1)AE＝CF；
证明：∵△ADF≌△CBE，∴∠AFD＝∠CEB.∴BE∥DF.
【2023·长沙】 【新考法·构造直角三角形法】如图，在▱ABCD中，DF平分∠ADC，交BC于点E，交AB的延长线于点F.(1)求证：AD＝AF；
证明：在▱ABCD中，∵AB∥CD，∴∠CDE＝∠F.∵DF平分∠ADC，∴∠ADE＝∠CDE.∴∠F＝∠ADF.∴AD＝AF.
(2)若AD＝6，AB＝3，∠A＝120°，求BF的长和△ADF的面积．
解：∵AD＝AF＝6，AB＝3，∴BF＝AF－AB＝3.如图，过点D作DH⊥FA，交FA的延长线于点H.∵∠BAD＝120°，∴∠DAH＝60°.
【2023·菏泽】如图，在▱ABCD中，AE平分∠BAD，交BC于点E，CF平分∠BCD，交AD于点F.求证：AE＝CF.
【 新考法·直观猜想法 】如图，分别以▱ABCD(∠CDA≠90°)的三边AB，CD，DA为斜边作等腰直角三角形，得到△ABE，△CDG，△ADF.
(1)如图①，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF. 请判断GF与EF的关系．
解：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠DAB＋∠ADC＝180°.∵△ABE，△CDG，△ADF都是等腰直角三角形，CD＝AB，∴DG＝CG＝AE＝BE，DF＝AF，∠CDG＝∠ADF＝∠BAE＝∠DAF＝45°，∠DFA＝90°.
∴EF＝FG，∠EFA＝∠GFD，∴∠GFD＋∠GFA＝∠EFA＋∠GFA，∴∠GFE＝∠DFA＝90°，∴GF⊥EF.综上，GF＝EF，GF⊥EF.
(2)如图②，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，(1)中结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
解：GF＝EF，GF⊥EF仍然成立．证明如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∵△ABE，△CDG，△ADF都是等腰直角三角形，CD＝AB，∴DG＝CG＝AE＝BE，DF＝AF，∠CDG＝∠ADF＝∠BAE＝∠DAF＝45°，∠DFA＝90°.
∵AB∥CD，∴∠BAE＋∠DAF＋∠EAF＋∠ADF＋∠FDC＝180°，∴∠EAF＋∠CDF＝45°.又∵∠CDF＋∠GDF＝45°，∴∠FDG＝∠EAF.