安徽专版2024春八年级数学下册第19章四边形19.3矩形菱形正方形19.3.3.2正方形的判定作业课件新版沪科版

这是一份安徽专版2024春八年级数学下册第19章四边形19.3矩形菱形正方形19.3.3.2正方形的判定作业课件新版沪科版，共35页。
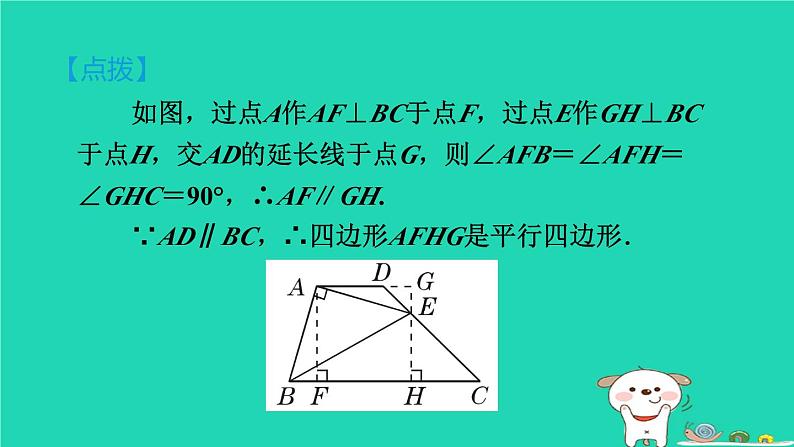
沪科版 八年级下第十九章 四边形矩形、菱形、正方形19.3.32 正方形的判定BCAA答 案 呈 现习题链接C在菱形ABCD中，若要添加一个条件，使它是正方形，则添加的条件可以是(　　) A．AB＝AD B．AB⊥BC C．AC⊥BD D．AC平分∠BAD 1【点拨】【答案】B在菱形ABCD中，若AB⊥BC，可根据有一个角是直角的菱形是正方形得菱形ABCD是正方形；而添加AB＝AD或AC⊥BD或AC平分∠BAD都不能判定菱形ABCD是正方形．2【2023·丽水】如图，在四边形ABCD中，AD∥BC，∠C＝45°，以AB为腰作等腰直角三角形BAE，顶点E恰好落在CD边上，若AD＝1，则CE的长是(　　) 【点拨】如图，过点A作AF⊥BC于点F，过点E作GH⊥BC于点H，交AD的延长线于点G，则∠AFB＝∠AFH＝∠GHC＝90°，∴AF∥GH.∵AD∥BC，∴四边形AFHG是平行四边形．∵∠AFH＝90°，∴四边形AFHG是矩形．∴∠G＝∠FAG＝90°.由题易知AB＝AE，∠BAE＝90°.∴∠FAG＝∠BAE.∴∠BAF＝∠EAG.∵∠AFB＝∠G＝90°，∴△AFB≌△AGE(AAS)．∴AF＝AG.∴矩形AFHG是正方形．∴AG＝GH.∵AG∥BC，∴∠EDG＝∠C＝45°.【答案】A3【2022·绍兴】 【新考法·动点探究法】如图，在平行四边形ABCD中，AD＝2AB＝2，∠ABC＝60°，E，F是对角线BD上的动点，且BE＝DF，M，N分别是边AD，边BC上的动点．下列4种说法：①存在无数个平行四边形MENF； ②存在无数个矩形MENF； ③存在无数个菱形MENF； ④存在无数个正方形MENF. 其中正确的有(　　) A．1种 B．2种 C．3种 D．4种 【点拨】连接AC，MN，AC交BD于点O.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD.∵BE＝DF，∴OE＝OF.当MN过点O时，易证OM＝ON，∴四边形MENF为平行四边形．∵点E，F，M，N是动点，∴存在无数个平行四边形MENF；当MN过点O，MN＝EF时，四边形MENF是矩形，∵点E，F，M，N是动点，∴存在无数个矩形MENF；当MN过点O，MN⊥EF时，四边形MENF是菱形，∵点E，F是动点，∴存在无数个菱形MENF；当MN过点O， MN＝EF且MN⊥EF时，四边形MENF是正方形，符合要求的正方形只有一个，故①②③正确，④错误．【答案】C4①②③④【2022·攀枝花】如图，以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF，且点A在△BCF内部，给出以下结论：①四边形ADFE是平行四边形； ②当∠BAC＝150°时，四边形ADFE是矩形； ③当AB＝AC时，四边形ADFE是菱形； ④当AB＝AC，且∠BAC＝150°时，四边形ADFE是正方形. 其中正确结论有__________(填上序号). 【点拨】①利用SAS证明△EFB≌△ACB，得到EF＝AC＝AD；同理可得△CDF≌△CAB，得出DF＝AB＝AE，根据两组对边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形，即可判断结论①正确；②当∠BAC＝150°时，易得∠EAD＝90°，结合①根据有一个角是90°的平行四边形是矩形即可判断结论②正确；③当AB＝AC时，易得AE＝AD，结合①根据有一组邻边相等的平行四边形是菱形即可判断结论③正确；④结合②，③根据正方形的判定：既是菱形，又是矩形的四边形是正方形即可判断结论④正确．5如图，点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，则下列说法中正确的个数是(　　) ①若AC＝BD，则四边形EFGH为矩形； ②若AC⊥BD，则四边形EFGH为菱形； ③若四边形EFGH是平行四边形，则AC与BD互相平分；④若四边形EFGH是正方形，则AC与BD互相垂直且相等. A．1 B．2 C．3 D．4 【点拨】【答案】A中点四边形的形状取决于原四边形两条对角线的位置关系和数量关系．两条对角线垂直→中点四边形是矩形，两条对角线相等→中点四边形是菱形，两条对角线互相垂直且相等→中点四边形是正方形．6如图，一个四边形顺次添加下列条件中的三个条件便得到正方形： a．两组对边分别相等　b．一组对边平行且相等c．一组邻边相等 d．一个角是直角 顺次添加的条件：①a→c→d；②b→d→c；③a→b→c，则正确的是(　　) A．①　　B．③　　C．①②　　D．②③ 【点拨】①由a得到两组对边分别相等的四边形是平行四边形，添加c得到一组邻边相等的平行四边形是菱形，再添加d得到有一个角是直角的菱形是正方形，故①正确；②由b得到一组对边平行且相等的四边形是平行四边形，添加d得到有一个角是直角的平行四边形是矩形，再添加c得到一组邻边相等的矩形是正方形，故②正确；【答案】C③由a，b都能得到四边形是平行四边形，再添加c得到一组邻边相等的平行四边形是菱形，不能得到四边形是正方形，故③不正确．【点方法】由矩形和菱形判定正方形，容易混淆二者需要添加的条件．由矩形得到正方形只需一组邻边相等，由菱形得到正方形只需一个角是直角．7【2022·邵阳】如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．求证：四边形AECF是正方形．证明：∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC，OB＝OD.∵BE＝DF，∴OE＝OF.∴四边形AECF是菱形．∵OE＝OA，∴OE＝OF＝OA＝OC，即EF＝AC.∴菱形AECF是正方形．8【2023·德阳】 【新考法·旋转法】将一副直角三角板DOE与AOC叠放在一起，如图①，∠O＝90°，∠A＝30°，∠E＝45°，OD>OC．在两个三角板所在平面内，将三角板DOE绕点O顺时针方向旋转α(0°