江苏省苏州市苏州高新区实验初级中学2023-2024年七年级下学期3月月考数学试题

这是一份江苏省苏州市苏州高新区实验初级中学2023-2024年七年级下学期3月月考数学试题，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．如图所示的图案可以看作由“基本图案”经过平移得到的是（ ）
A．B．C．D．
2．下列命题中，假命题是（ ）
A．对顶角相等B．不相等的两个角不是对顶角
C．两直线平行，内错角相等D．同旁内角互补
3．如图，直线被直线所截，，则的度数是（ ）
（第3题图）
A．B．C．D．
4．如图，的大小是（ ）
（第4题图）
A．B．C．D．
5．如图，为估计池塘岸边之间的距离，在池塘的一侧选取一点，测得米，米，之间的距离不可能是（ ）米
（第5题图）
A．5米B．10米C．15米D．20米
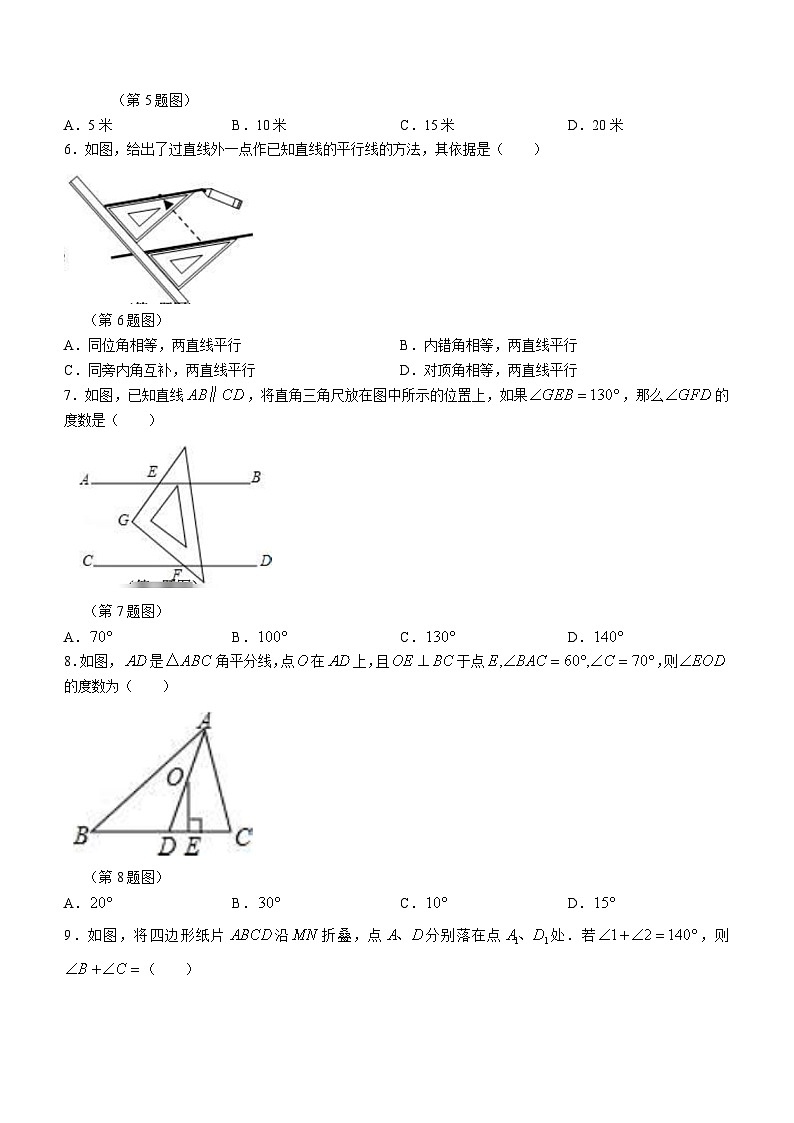
6．如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（ ）
（第6题图）
A．同位角相等，两直线平行B．内错角相等，两直线平行
C．同旁内角互补，两直线平行D．对顶角相等，两直线平行
7．如图，已知直线，将直角三角尺放在图中所示的位置上，如果，那么的度数是（ ）
（第7题图）
A．B．C．D．
8．如图，是角平分线，点在上，且于点，则的度数为（ ）
（第8题图）
A．B．C．D．
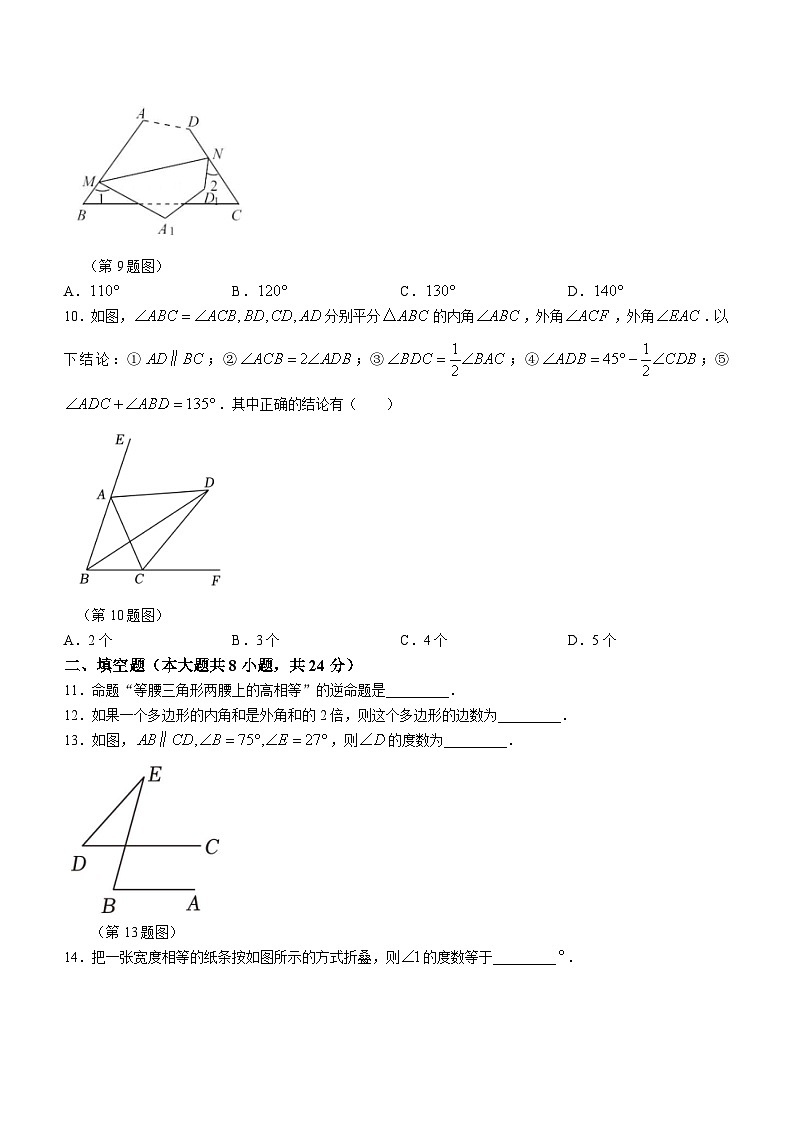
9．如图，将四边形纸片沿折叠，点分别落在点处．若，则（ ）
（第9题图）
A．B．C．D．
10．如图，分别平分的内角，外角，外角．以下结论：①；②；③；④；⑤．其中正确的结论有（ ）
（第10题图）
A．2个B．3个C．4个D．5个
二、填空题（本大题共8小题，共24分）
11．命题“等腰三角形两腰上的高相等”的逆命题是_________．
12．如果一个多边形的内角和是外角和的2倍，则这个多边形的边数为_________．
13．如图，，则的度数为_________．
（第13题图）
14．把一张宽度相等的纸条按如图所示的方式折叠，则的度数等于_________．
（第14题图）
15．在中，，点在边上，连接，若为直角三角形，则的度数为_________．
16．下列命题中，①同位角相等；②三角形的高相交于三角形的内部；③三角形的一个外角大于任意一个内角；④一个多边形的边数每增加一条，这个多边形的内角和就增加；⑤两个角的两边分别平行，则这两个角相等．真命题的有_________个．
17．如图，在中，是的中点，是上的一点，且与相交于点，若的面积为12，则的面积为_________．
（第17题图）
18．如图，点在延长线上，交于点，且比的余角大为线段上一动点，为上一点，且满足为的平分线．下列结论：
①；②；③平分；④；⑤．其中结论正确的序号是_________．
（第18题图）
三、解答题（本大题共9小题，共56分）
19．如图，在每个小正方形边长为1的方格纸内将经过一次平移后得到，图中标出了点的对应点．
根据下列条件，利用格点和三角尺画图：
（1）补全；
（2）请在边上找一点，使得线段平分的面积，在图上作出线段；
（3）利用格点在图中画出边上的高线；
（4）找（要求各顶点在格点上，不与点重合），使其面积等于的面积．满足这样条件的点共_________个．
20．填空，将本题补充完整．
如图，已知，将求的过程填写完整．
解：（已知），
_________，
又（已知），
_________（等量代换），
（_________），
（_________），
（已知），
_________．
21．如图，在中，平分，交于，
（1）若，求的度数．
（2）若于点，求的度数．
22．在一个各内角都相等的多边形中，每一个内角都比相邻外角的3倍还大，求这个多边形的边数．
23．已知等腰三角形的周长为，一腰上的中线把等腰三角形分成周长之差为的两个三角形，求等腰三角形的腰长．
24．如图，已知．
（1）请你判断与的位置关系，并证明你的结论；
（2）若平分，试求的度数．
25．如图，在中，平分为线段上的一个动点，交直线于点．
（1）若，求的度数；
（2）当点在线段上运动时，猜想与的数量关系，写出结论并证明．
26．如果三角形的两个内角与满足，那么我们称这样的三角形为“准直角三角形”．
图1 图2
（1）关于“准直角三角形”，下列说法：
①在中，若，则是准直角三角形；
②若是“准直角三角形”，，则；
③“准直角三角形”一定是针角三角形．
其中，正确的是_________．（填写所有正确结论的序号）
（2）如图①，在中，是的角平分线．
求证：是“准直角三角形”．
（3）如图②，为直线上两点，点在直线外，且．若是上一点，且是“准直角三角形”，请直接写出的度数．
27．（1）如图1，，点分别在直线上，，过点作交于点，平分平分与交于点．
图1 图2
①_________；
②若，求；
（2）如图2将②中确定的绕着点以每秒的速度逆时针旋转，旋转时间为保持不变，当边与射线重合时停止，则在旋转过程中，的边所在的直线与的某一边所在的直线垂直时，直接写出此时的值．
2023—2024学年苏州新区实验中学七年级月考数学试题
参考答案与解析
一、单选题（本大题共10小题，共20分）
1．解：A、不是由“基本图案”经过平移得到，故此选项不符合题意；
B、是由“基本图案”经过平移得到，故此选项符合题意；
C、不是由“基本图案”经过平移得到，故此选项不符合题意；
D、不是由“基本图案”经过平移得到，故此选项不符合题意；
故选：B．
2．解：A、对顶角相等，正确，是真命题，不符合题意；
B、不相等的两个角不是对顶角，正确，不符合题意；
C、两直线平行，同旁内角互补，故原命题错误，符合题意
D、两直线平行，内错角相等，正确，不符合题意；
故选：C．
3．【解答】解：，，
，
故选：D．
4．【解答】解：，，
是的一个外角，，
．
故选：B．
5．【解答】解：之间的距离，之间的距离，
即之间的距离取值在米（不包括5米和25米），
所以之间的距离不可能是5米．
故选：A．
6．【解答】解：如图，给出了过直线外一点作已知直线的平行线的方法，其依据是同位角相等，两直线平行．
故选：A．
7．【解答】解：过点作，
，，，
，，
，，
故选：D．
8．【解答】解：，．
又是的角平分线，
，，
又，．
故选：C．
9．【解答】解：，
．
，
．
故选：A．
10．【解答】解：①平分，，
，
，，
，故①正确，
②，，
平分，，
，故②正确；
③，
，
，，
，
，
，，故③正确；
④平分，，
，，，
平分，，
，
，
，，、
，故④正确；
⑤由④得，，
，，
，故⑤不正确．
故选：C．
二、填空题（本大题共8小题，共24分）
11．【解答】解：命题“等腰三角形两腰上的高相等”的逆命题是两边上的高相等的三角形为等腰三角形．
故答案为：两边上的高相等的三角形为等腰三角形．
12．【解答】解：设这个多边形边数为，内角和为，
多边形外角和为，
解得：，
故答案为：6．
13．【解答】解：如图，
，，
是的外角，，
，
故答案为：．
14．【解答】解：由翻折不变性可知：，
，，
，，
故答案为65．
15．【解答】解：分两种情况：
图1 图2
（1）如图1，当时，
，；
（2）如图2，当时，
，，
，
故答案为：或，
16．【解答】解：①只有两平行直线被第三条直线所截时，同位角才相等，故说法①错误；
②只有锐角三角形的三条高相交于三角形的内部，故说法②错误；
③三角形的一个外角大于任意一个和它不相邻的内角，故说法③错误；
④一个多边形的边数每增加一条，这个多边形的内角和就增加，此说法④正确：
⑤两个角的两边分别平行，则这两个角可能相等，也可能互补，故说法⑤错误；
故答案为：1个．
17．【解答】解：如图，连接．
是中点，，，
又，，
设，则，，
，，
，，
，．
．
故答案为：40．
18．【解答】解：①，，结论①正确；
②，．
，，
，结论②正确；
③，．
，，
平分，结论③正确；
④，．
比的余角大，．
，
，结论④正确；
⑤为的平分线，
．
，
，结论⑤正确．
故答案为：①②③④⑤．
三、解答题（本大题共9小题，共56分）
19．【解答】（1）如图所示，即为所求．
（2）如图所示，线段即为所求；
（3）如图所示，即为所求；
（4）如图所示，满足这样条件的点共6个．
故答案为：6．
20．【解答】解：（已知），，
又（已知），
（等量代换），
（内错角相等，两直线平行），
（两直线平行，同旁内角互补），
（已知），
．
故答案为：；内错角相等，两直线平行；；两直线平行，同旁内角互补；105．
21．【解答】解：（1） （2）
22．【解答】解：设多边形的一个外角为，则与其相邻的内角等于，
由题意，得，解得，
即多边形的每个外角为，
又多边形的外角和为，
多边形的外角个数，
多边形的边数．
23．【解答】解：设腰长为，底边长为．
（1）若腰比底边长，根据题意得，解得；
（2）若底边比腰长，根据题意得，解得．
故这个三角形的腰长是或．
24．【解答】解：（1），理由：
，，，
又，，．
（2），，
又平分，，，
又，，
25．【解答】解：（1），
，平分，，
，；
（2）．设，
平分，，
，
，，
，
，
，，
．
26．【解答】（1）解：①，
不是“准直角三角形”，①不正确；
②，②正确；
③三角形为“准直角三角形”，则它的两个内角与满足，
，设它的第三个内角为，
，
一定是针角，“准直角三角形”一定是针角三角形，
③正确，
故答案为：②③．
（2）证明：如图1，，，
是的角平分线，，
，是“准直角三角形”．
（3）解：如图2，若点在点右侧，是“准直角三角形”，且，
图2
，，
，；
若点在点右侧，是“准直角三角形”，且，
，，；
若点在点右侧，是“准直角三角形”，且，
，，，
；
若点在点右侧，是“准直角三角形”，且，
，，，
综上所述，的度数为或或或．
27．【解答】解：（1）①平分平分，
，
，，
又，
故，
即，
，
，
故答案为：45；
②，，
，，
又，，
故，
解得：，故，
；
（2）由②可得，
当时，如图：
，，
，
此时旋转时间为；
当时，如图：
，
，
，
此时旋转时间为；
当时，如图：
，，
，，
，
此时旋转时间为；
综上，符合条件的的值为17.5秒或37.5秒或40秒．