




2024年辽宁省鞍山市台安县部分学校中考模拟(一模)数学试题(原卷版+解析版)
展开考生注意:所有试题必须在答题卡指定区域内作答,在本试卷上作答无效
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到“-1”分,则该队在比赛中( )
A. 与对手打成平局B. 输给对手C. 打赢了对手D. 无法确定
【答案】B
【解析】
【分析】根据正负数的概念即可得出答案.
【详解】解:由题意可知:胜一场记作“+1”分,平局记作“0”分,
∴某队得到“-1”分,则球队比赛输给了对手.
故选:B.
【点睛】本题考查了正数和负数概念,解题的关键是理解正数和负数的意义.
2. 如图所示的几何体的主视图是( )
A. B.
C. D.
【答案】D
【解析】
【分析】根据从正面看的图为主视图进行判断即可.
【详解】解:几何体的主视图有三列,左边一列有一层,中间一列有2层,右边一列有1层,
因此看到的主视图为,故D正确.
故选:D.
【点睛】本题主要考查了三视图,解题的关键是熟练掌握主视图为从正面看到的图形,俯视图为从上面看到的图形,左视图为从左面看到的图形.
3. 下列图形既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】利用轴对称图形和中心对称图形的特征进行判断.
【详解】A、是轴对称图形,不合题意;
B、是中心对称图形,不合题意;
C、既是轴对称图形又是中心对称图形,符合题意;
D、是轴对称图形,不合题意;
故选:C.
【点睛】本题考查轴对称图形和中心对称图形的识别,解题的关键是分别确定轴对称和对称中心.
4. 下列运算正确的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据合并同类项,同底数幂的乘法,同底数幂的除法,积的乘方进行计算即可求解.
【详解】解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意.
故选:D.
【点睛】本题考查了合并同类项,同底数幂的乘法,同底数幂的除法,积的乘方,熟练掌握合并同类项,同底数幂的乘法,同底数幂的除法,积的乘方的运算法则是解题的关键.
5. 一元二次方程根的情况是( )
A. 有两个相等的实数根B. 有两个不相等的实数根
C. 没有实数根D. 不能确定
【答案】C
【解析】
【分析】根据一元二次方程根的判别式判断即可.
【详解】由题意可知该方程,
∴,
∴该方程没有实数根.
故选C.
【点睛】本题考查根据一元二次方程根的判别式判断其根的情况.掌握一元二次方程的根的判别式为,且当时,该方程有两个不相等的实数根;当时,该方程有两个相等的实数根;当时,该方程没有实数根是解题关键.
6. 分式方程的解为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据分式方程的解法解题即可.
详解】
经验证:x=1是方程根.
故选B.
【点睛】本题考查分式方程的计算,关键在于掌握解方程的步骤.
7. 一次函数中,若kb<0,且y随x的增大而减小,则其图象可能是( )
A. B. C. D.
【答案】A
【解析】
【分析】由y随着x的增大而减小,利用一次函数的性质可得出k<0,结合kb<0可得出b>0,再利用一次函数图象与系数的关系即可得出一次函数y=kx+b的图象经过第一、二、四象限.
【详解】解:∵y随x的增大而减小,
∴k<0,
∵kb<0,
∴b>0,
∴一次函数y=kx+b的图象经过第一、二、四象限;
故选:A
【点睛】本题考查了一次函数的性质以及一次函数图象与系数的关系,牢记“k<0,b>0⇔y=kx+b的图象在一、二、四象限”是解题的关键.
8. 我国古代数学的经典著作《九章算术》中有一道“盈不足术”问题:“今有共买羊,人出五,不足四十五:人出七,不足三.问人数、羊价各几何?”译文:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱.问合伙人数、羊价各是多少?该问题中的羊价为( )
A. 21钱B. 65钱C. 150钱D. 165钱
【答案】C
【解析】
【分析】根据人数乘以每人出钱数加差价可列出方程,解方程即可.
【详解】根据题意可列方程组,设人数为x人,
则:,
解得:x=21,
5×21+45=150,
故选C.
【点睛】本题考查一元一次方程的应用,也可用二元一次方程组解决,能够找到等量关系是解决本题的关键.
9. 如图所示的是一辆自动变速自行车的实物图,图2是抽象出来的部分示意图,已知直线与相交于点,,则的大小为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据三角形的外角的性质得出,根据平行线的性质即可求解.
【详解】解:∵,
∴,
∵,
∴,
故选:B.
【点睛】本题考查了三角形外角的性质,平行线的性质,熟练掌握以上知识是解题的关键.
10. 如图,已知菱形的顶点,,按以下步骤作图:①分别以点和点为圆心,大于的长为半径画弧,两弧交于点,;②作直线,且恰好经过点,与交于点.则点的坐标为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据作图过程可知垂直平分,连接,如图,则可根据线段垂直平分线的性质和菱形的性质证明是等边三角形,从而可得,过点作轴于点E,在直角△ADE中易知AD=2,再利用60°的三角函数求出AE与DE的长即得答案.
【详解】解:根据作图过程可知:垂直平分,连接,过点作轴于点.
∵垂直平分,
∴,.
∵,
∴AB=BC=AC,即是等边三角形.
∴.
∴.
在中,∵,,
∴点的坐标为.
故选B.
【点睛】本题考查了尺规作线段的垂直平分线、菱形的性质、等边三角形的判定与性质、解直角三角形等知识,考查的知识点虽多,但难度不大,根据题意正确判断是等边三角形是求解的关键.
第二部分 非选择题(共90分)
二、填空题(本题共5小题,每小题3分,共15分)
11. 计算 的结果等于_________.
【答案】
【解析】
【分析】利用平方差公式进行计算即可.
【详解】
故填13.
【点睛】本题考查平方差公式及二次根式的运算,熟练掌握公式是解题关键.
12. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置,,,平移距离为6,则阴影部分面积为_______.
【答案】48
【解析】
【分析】本题考查的是全等三角形的性质、平移的性质,掌握全等形的面积相等是解题的关键.
根据平移的性质分别求出、,根据题意求出,根据全等三角形的性质、梯形的面积公式计算,得到答案.
【详解】解:由平移的性质知,,,
,
,
,
,
故答案为48
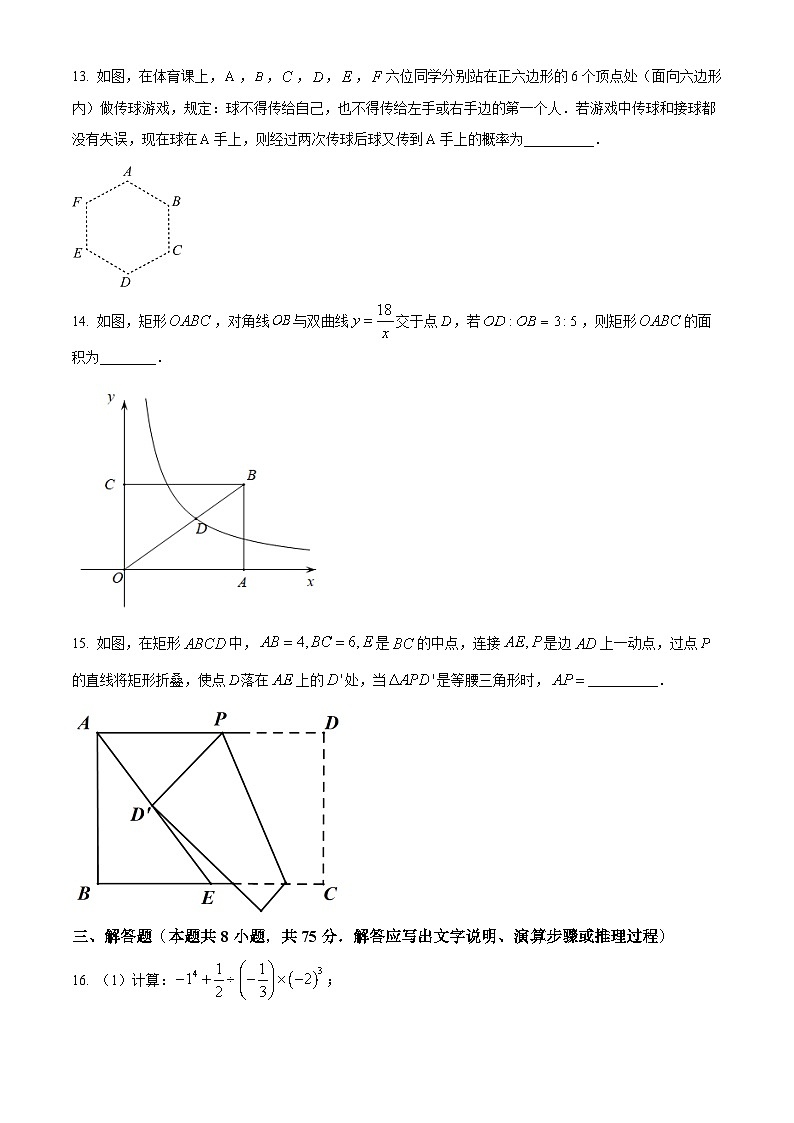
13. 如图,在体育课上,,,,,,六位同学分别站在正六边形的6个顶点处(面向六边形内)做传球游戏,规定:球不得传给自己,也不得传给左手或右手边的第一个人.若游戏中传球和接球都没有失误,现在球在手上,则经过两次传球后球又传到手上的概率为__________.
【答案】
【解析】
【分析】根据题意画树状图,可得两次传球共有9种等可能结果,球又回到A手上的结果数为3种,再根据概率公式求解即可.
【详解】根据题意画树状图如下:
由树状图可知,两次传球共有9种等可能结果,球又回到A手上的结果数为3种,
∴经过两次传球后球又传到手上的概率为,
故答案为:.
【点睛】本题考查了用列表法或树状图求概率,概率公式,准确理解题意,熟练掌握知识点是解题的关键.
14. 如图,矩形,对角线与双曲线交于点,若,则矩形的面积为________.
【答案】50
【解析】
【分析】根据反比例函数系数k的几何意义可得S△ODE=9,利用相似三角形的性质,可得S△ADE:S△OBA=9:25,进而求出S△OBA=25,由矩形的性质得到答案.
【详解】解:过点D作DE⊥OA,垂足为E,则S△ODE=×18=9,
∵是矩形
∴AB⊥AO
∴DEAB,
∴△ODE∽△OBA,
∵
∴S△ADE:S△OBA=9:25,
∴S△OBA=25,
∴矩形OABC的面积为25×2=50,
故答案为:50.
【点睛】本题考查反比例函数系数k的几何意义,相似三角形以及矩形的性质,理解反比例函数系数k的几何意义以及相似三角形的性质是解决问题的关键.
15. 如图,在矩形中,是的中点,连接是边上一动点,过点的直线将矩形折叠,使点落在上的处,当是等腰三角形时,__________.
【答案】3或或
【解析】
【分析】根据矩形的性质得到AD=BC=6,∠BAD=∠D=∠B=90°,根据勾股定理得到AE=5,设AP=x,则PD′=PD=6-x,当△APD′是等腰三角形时,分三种情况分别求解即可.
【详解】∵在矩形ABCD中,AB=4,BC=6,
∴AD=BC=6,∠BAD=∠D=∠B=90°,
∵E是BC的中点,
∴BE=CE=3,
∴,
∵沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,
∴PD′=PD,
设AP=x,则PD′=PD=6-x,
当△APD′是等腰三角形时,可分三种情况讨论:
①若,则,
解得x=3;
②若,如图,过点作⊥AD于点F,
∵AD∥BC,
∴,
∴,,
∴,,
∴,
在Rt△中,,
解得,(不合题意,舍去);
③若,如图,过点作⊥AD于点F,
∵,
∴,
∴,
∴,
∴,
解得;
综上,AP的值为3或或.
【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理、锐角三角函数等知识,正确的理解题意并分类讨论是解题的关键.
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16. (1)计算:;
(2)化简:.
【答案】(1)11;(2)
【解析】
【分析】本题主要考查了含乘方的有理数混合计算,分式的混合计算:
(1)按照先计算乘方,再计算乘除法,最后计算加法的运算顺序求解即可;
(2)根据分式的混合计算法则求解即可.
【详解】解:(1)原式
.
(2)原式
.
17. 照明灯具经过多年的发展,大致历经白炽灯、节能灯、灯三个阶段,目前性价比最高的是灯,不仅更节能,而且寿命更长,同时也更加环保.某商场计划购进甲、乙两种型号的照明灯共200只,甲型号照明灯的进价为30元/只,乙型号照明灯的进价为60元/只.
(1)若购进甲、乙两种型号的照明灯共用去7200元,求甲、乙两种型号照明灯各购进多少只.
(2)若商场准备用不多于8400元购进这两种型号的照明灯,问:甲型号照明灯至少购进多少只?
【答案】(1)甲型号照明灯购进160只,乙型号照明灯购进40只
(2)甲型号照明灯至少购进120只
【解析】
【分析】本题主要考查了二元一次方程组的实际应用,一元一次不等式的实际应用:
(1)设甲型号照明灯购进x只,乙型号照明灯购进y只,根据购进甲、乙两种型号的照明灯共200只共花费7200元列出方程组求解即可;
(2)设甲型号照明灯购进m只,则乙型号照明灯购进只,根据总费用不超过8400元列出不等式求解即可.
【小问1详解】
解:设甲型号照明灯购进x只,乙型号照明灯购进y只.
根据题意,得
解得
答:甲型号照明灯购进160只,乙型号照明灯购进40只.
【小问2详解】
解:设甲型号照明灯购进m只,则乙型号照明灯购进只.
根据题意,得,
解得.
答:甲型号照明灯至少购进120只.
18. 【数据收集与整理】
根据国家统计局统一部署,衢州市统计局对2022年我市人口变动情况进行了抽样调查,抽样比例为.根据抽样结果推算,我市2022年的出生率为,死亡率为,人口自然增长率为,常住人口数为人(表示千分号).(数据来源:衢州市统计局)
【数据分析】
(1)请根据信息推测人口自然增长率与出生率、死亡率的关系;
(2)已知本次调查的样本容量为11450,请推算的值;
(3)将我市及全国近五年的人口自然增长率情况绘制成如下统计图.根据统计图分析:
①对图中信息作出评判(写出两条);
②为扭转目前人口自然增长率的趋势,请给出一条合理化建议.
【答案】(1)人口自然增长率出生率死亡率
(2)
(3)①我国近五年的人口自然增长率逐年下降;自2021年以来,衢州市得人口呈负增长(答案不唯一);
②建议国家加大政策优惠,鼓励人们多生育(答案不唯一)
【解析】
【分析】(1)根据题意,可得人口自然增长率等于出生率减死亡率;
(2)根据样本容量总体抽样比例求出的值即可;
(3)①根据统计图进行解答,合理即可;
②根据目前人口自然增长率的趋势,提出合理建议,即可解答.
【小问1详解】
解:根据题意可知,人口自然增长率出生率死亡率;
【小问2详解】
解:由题意,可得,
解得;
【小问3详解】
解:①我国近五年的人口自然增长率逐年下降;自2021年以来,衢州市得人口呈负增长;
②建议国家加大政策优惠,鼓励人们多生育.
【点睛】本题考查了总体,合体,样本,样本容量,折线统计图,用调查作决策,看懂折线图,并熟知上述概念之间的联系是解题的关键.
19. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位()是时间()的一次函数,下表是小明记录的部分数据,其中有一个h的值记录错误.
解答下列问题:
(1)记录错误的的值是__________,正确的值应该是__________;
(2)求水位()与时间()的一次函数关系式;
(3)当为时,求对应的时间为多少.
【答案】(1);
(2)
(3)
【解析】
【分析】本题考查一次函数的应用;
(1)由表格中数据知,时间每增加分钟,增加,据此可知是错误的值;
(2)设水位()与时间()的一次函数关系式为,再用待定系数法求解析式即可;
(3)利用(2)的关系式求解值即可.
【小问1详解】
解:由表格中数据知,时间每增加分钟,增加,
是错误的值,正确的值应该是
故答案为:,;
【小问2详解】
解:设水位()与时间()的一次函数关系式为,
代入表中数据得,
解得,
∴水位()与时间()的一次函数关系式为;
【小问3详解】
解:由(2)知,
当时,,
解得,
故答案为:.
20. 在学校的数学学科周上,李老师指导学生测量学校旗杆的高度.在旗杆附近有一个斜坡,坡长米,坡度,小华在处测得旗杆顶端的仰角为,在处测得旗杆顶端的仰角为.求旗杆的高度.(点,,,在同一平面内,,在同一水平线上,结果保留根号)
【答案】米
【解析】
【分析】本题考查的是解直角三角形的应用:仰角俯角、坡度坡角问题,勾股定理,根据题意作出辅助线,构造出直角三角形是解题的关键.
过点D作,垂足为,过点D作,垂足为,依据题意得:,,设米,则米,在中,利用勾股定理求出、的长.再设米,则米,最后分别在和中利用锐角三角函数的定义求出和的长,从而列出关于的方程即可求解.
【详解】解:过点D作,垂足为,过点D作,垂足为,
依据题意得:,,
坡长米,坡度,
,
设米,则米,
在中,
(米),
,解得:,
米,则米,
设米,
米,
在中,,
(米),
在中,,
米,
,
,
解得:,
(米),
旗杆的高度为米.
21. 如图,在中,,点D,E,F分别是边,,上的点,以为直径的半圆O经过点E,F,且平分.
(1)求证:是半圆O的切线;
(2)若,,求的长.
【答案】(1)见解析 (2)2
【解析】
【分析】(1)连接,证明得到即可得到证明;
(2)连接,先证得到,结合角所对直角边等于斜边一半得到,即可得到答案;
【小问1详解】
证明:连接,
平分,
,
,
,
,
,
,
,
是的半径,
是半圆的切线;
【小问2详解】
解:,,,
,,
,
,
,
,
∵是半圆O的直径,
∴,
∴,
∴,
,
,
;
【点睛】本题考查切线的证明,直角三角形角所对直角边等于斜边一半,角平分线定义,解题的关键作出辅助线得到,.
22. 乒乓球被誉为中国国球.2023年的世界乒乓球锦标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.图2是图1所示乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度(距离球台的高度)为的点A处,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为y(单位:),乒乓球运行的水平距离记为x(单位:).测得如下数据:
(1)如图3,在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象.
(2)①当乒乓球到达最高点时,与球台之间的距离是______,当乒乓球落在对面球台上时,到起始点的水平距离是______.
②求满足条件的抛物线的表达式.
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练,如图2,乒乓球台长为,球网高为.现在已经计算出乒乓球恰好过网的击球高度的值约为.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
【答案】(1)见解析 (2)①49,230;②
(3)乒乓球恰好落在对面球台边缘点B处时,击球高度的值为
【解析】
【分析】本题主要考查了二次函数的实际应用:
(1)根据描点法画出函数图象即可求解;
(2)①根据二次函数图象的对称性求得对称轴以及顶点,根据表格数据,可得当时,;
②待定系数法求解析式即可求解;
(3)根据题意,设平移后的抛物线的解析式为,根据题意当时,,代入进行计算即可求解.
【小问1详解】
解:如图所示,
【小问2详解】
解:①观察表格数据,可知当和时,函数值相等,则对称轴为直线,顶点坐标为,
又抛物线开口向下,可得最高点时,与球台之间的距离是,
当时,,
∴乒乓球落在对面球台上时,到起始点的水平距离是;
故答案为:;.
②设抛物线解析式为,将代入得,
,
解得:,
∴抛物线解析式为;
小问3详解】
解:∵当时,抛物线的解析式为,
设乒乓球恰好落在对面球台边缘点B处时,击球高度的值为,则平移距离为,
∴平移后的抛物线的解析式为,
依题意,当时,,
即,
解得:.
答:乒乓球恰好落在对面球台边缘点B处时,击球高度的值为.
23. 综合与实践
问题情境:数学课上,同学们以特殊四边形为基本图形,添加一些几何元素后探究图形中存在的结论.已知在中,,的平分线交边于点E,交边的延长线于点F,以为邻边作.
特例探究:(1)如图1,“创思”小组的同学研究了四边形为矩形时的情形,发现四边形是正方形,请你证明这一结论;
(2)“敏学”小组的同学在图1基础上连接,得到图2,发现图2中线段与之间存在特定的数量关系,请你帮他们写出结论并说明理由;
拓展延伸:(3)“善问”小组的同学计划对展开类似研究.如图3,在中,.
请从下面A,B两题中任选一题作答.我选择________题.
A:当,时,请补全图形,并直接写出A,G两点之间的距离.
B:当时,请补全图形,并直接写出以A,C,G为顶点的三角形面积的最小值.
【答案】(1)见解析;(2)见解析;(3)A:;B:
【解析】
【分析】(1)根据矩形的性质即角平分线的性质证明即可;
(2)连接交于点O,连接,由(1)得四边形为正方形,,由线段垂直平分线的性质即可得到结论;
(3)A:过点G作交于点H,连接,证明四边形为是菱形,由锐角三角函数得到,,进而得到,利用勾股定理即可求解;
B:连接,交于点H,当时,最短,此时的面积最小,利用锐角三角函数求出,即可求解.
【详解】解:(1)证明:∵四边形为矩形,
,
,
∵四边形平行四边形,
∴平行四边形为矩形,
∵平分,
,
,
,
∴矩形为正方形;
(2),理由:连接交于点O,连接,
∵由(1)得四边形为正方形,
,
垂直平分,
,
∵四边形为矩形,
,
;
(3)A:补全图形如下:过点G作交于点H,连接,
由题意得四边形为平行四边形,
,平分,
,
,,,
,
,
,,
,,
,
,
,
,
四边形为是菱形,
,
,,
,
,
此时,A,G两点之间的距离为;
B:补全图形如下: 连接,交于点H,
由A的证明知四边形为是菱形,
,
,
当时,最短,此时的面积最小,
,,
,
,
四边形为是菱形,
,,
,
,,
,
,
以A,C,G为顶点的三角形面积的最小值为.
【点睛】本题考查四边形综合题、锐角三角函数、勾股定理、平行四边形的性质、菱形的判定和性质等知识,解题的关键是准确寻找全等三角形解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.()
()
水平距离
0
10
50
90
130
170
230
竖直高度
33
45
49
45
33
0
2024年辽宁省沈阳市部分学校 中考模拟(一模)数学模拟试题(原卷版+解析版): 这是一份2024年辽宁省沈阳市部分学校 中考模拟(一模)数学模拟试题(原卷版+解析版),文件包含精品解析2024年辽宁省沈阳市部分学校中考模拟一模数学模拟试题原卷版docx、精品解析2024年辽宁省沈阳市部分学校中考模拟一模数学模拟试题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
2024年辽宁省部分学校中考模拟(一模)数学模拟试题(原卷版+解析版): 这是一份2024年辽宁省部分学校中考模拟(一模)数学模拟试题(原卷版+解析版),文件包含精品解析2024年辽宁省部分学校中考模拟一模数学模拟试题原卷版docx、精品解析2024年辽宁省部分学校中考模拟一模数学模拟试题解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
辽宁省鞍山市台安县部分学校2023-2024年中考模拟(一模)数学试题.1: 这是一份辽宁省鞍山市台安县部分学校2023-2024年中考模拟(一模)数学试题.1,共12页。












