2.3　分式方程 习题精练+知识讲解 2024年河北版中考数学一轮复习课件

这是一份2.3　分式方程 习题精练+知识讲解 2024年河北版中考数学一轮复习课件，文件包含23分式方程知识讲解pptx、23分式方程习题精练pptx等2份课件配套教学资源，其中PPT共51页， 欢迎下载使用。
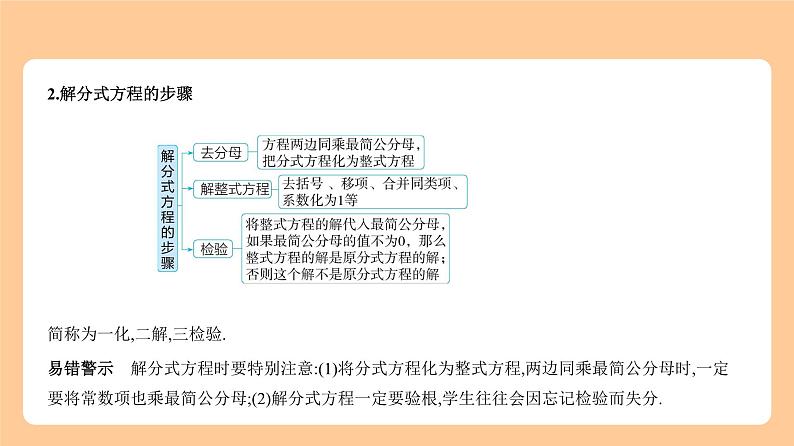
2.解分式方程的步骤 简称为一化,二解,三检验.
易错警示　解分式方程时要特别注意:(1)将分式方程化为整式方程,两边同乘最简公分母时,一定 要将常数项也乘最简公分母;(2)解分式方程一定要验根,学生往往会因忘记检验而失分.
3.分式方程增根的两个特征(1)增根使②　最简公分母    为0;(2)增根是分式方程化成的③　整式方程    的根.
1.下列方程:① =2;② = ;③ =1;④ + =4.其中分式方程是　①④    .
2.若关于x的分式方程 +1= 有增根,则m的值为    1    .
3.解方程:(1) = -2;(2) - =1.
考点2　分式方程的实际应用
1.列分式方程解应用题的一般步骤
2.列分式方程解应用题的常见题型(1)工程问题基本数量关系: =工作时间.常见等量关系: - =时间差; - =时间差(甲的工作效率比乙的低).特别地,有时工作总量可以看作“1”,这时, =工作效率.(2)盈利问题基本数量关系: =数量.
(3)行程问题基本数量关系: =时间.常见等量关系: - =时间差.
4.市政府为残疾人办实事,在某一道路改造工程中,为盲人修建一条长3 000米的盲道,根据规划设 计和要求,该市工程队在实际施工时增加了施工人员,每天修建的盲道长度比原计划增加了50%, 结果提前2天完成工程.问实际每天修建盲道多少米?
答案　实际每天修建盲道750米.
5.为了迎接“劳动节”的购物高峰,某运动品牌专卖店准备购进甲、乙两款运动鞋,其中甲款运动 鞋每双的进价比乙款运动鞋每双的进价高20元,且用3 000元购进甲款运动鞋的双数与用2 400元 购进乙款运动鞋的双数相同.求甲、乙两款运动鞋每双的进价分别是多少元.
答案　甲款运动鞋每双的进价是100元,乙款运动鞋每双的进价是80元.
6.班级组织同学乘大巴车前往研学基地开展爱国教育活动,基地离学校有90千米,队伍8:00从学校 出发.张老师因有事,8:30从学校自驾小车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果 比队伍提前15分钟到达基地.(1)大巴车与小车的平均速度分别是多少?(2)张老师追上大巴车的地点距离基地有多远?
答案    (1)大巴车的平均速度是40千米/时,小车的平均速度是60千米/时.(2)30千米.
一、依据分式方程解的特征确定字母参数的方法例1    (2022黑龙江龙东地区)已知关于x的分式方程 - =1的解是正数,则m的取值范围是 (　    )A.m>4　    B.m4且m≠5　    D.m0,解得m>4.∵x-1≠0,∴x≠1,即m-4≠1,解得m≠5.综上,m的取值范围是m>4且m≠5.故选C.
方法归纳　已知分式方程解的特征确定字母参数的值或范围时,首先将分式方程化为整式方程,用 含字母参数的代数式表示未知数,再根据解的特征确定字母参数的值或范围.同时要注意原分式方 程的最简公分母不能为零.
变式1(2022黑龙江齐齐哈尔)若关于x的分式方程 + = 的解大于1,则m的取值范围是    m>0且m≠1    .
解析　将分式方程两边同乘(x+2)(x-2),得(x+2)+2(x-2)=x+2m,解得x=m+1.∵m+1≠2,m+1≠-2,∴m≠1且m≠-3.∵x>1,∴m+1>1,解得m>0.综上,m的取值范围是m>0且m≠1.
二、依据分式方程有增根或无解确定字母参数的值的方法例2    (2021四川宜宾)若关于x的分式方程 -3= 有增根,则m的值是 (　    )A.1　    B.-1　    C.2　    D.-2答案    C解题思路     
解析    将分式方程两边同时乘(x-2)得,x-3(x-2)=m,解得x=3- m.∵分式方程有增根,∴x-2=0,∴x=2,∴3- m=2,∴m=2.故选C.
方法归纳　解决增根问题:第一步:令最简公分母为0,求出分式方程的增根;第二步:将增根代入去分母后得到的整式方程中,求出参数的值.解决无解问题:无解分两种情况.情况一:原分式方程去分母后得到的整式方程无解;情况二:分式方程有增根. 
变式2-1(2022黑龙江牡丹江)若关于x的方程 =3无解,则m的值为 (    B    )A.1　    B.1或3　    C.1或2　    D.2或3
解析　将方程两边同乘(x-1),得mx-1=3x-3,∴(m-3)x=-2.当m-3=0,即m=3时,整式方程无解.当x-1=0时,原分式方程有增根,把x=1代入(m-3)x=-2,得m-3=-2,解得m=1.综上,当m=1或3时,原方程无解.
变式2-2(2023四川巴中)关于x的分式方程 + =3有增根,则增根是m=　-1    .
解析　方程两边同乘(x-2),得x+m+(-1)=3(x-2),∴m=2x-5,∵原方程有增根,∴x-2=0,∴x=2,∴m=2x-5=-1.故答案为-1.
三、列分式方程解应用题例3    (2022山东聊城)为了解决雨季时城市内涝的难题,我市决定对部分老街道的地下管网进行改 造.在改造一段长3 600米的街道地下管网时,每天的施工效率比原计划提高了20%,按这样的进度 可以比原计划提前10天完成任务.(1)求实际施工时,每天改造管网的长度;(2)施工进行20天后,为了减少对交通的影响,施工单位决定再次加快施工进度,以确保总工期不超 过40天,那么以后每天改造管网至少还要增加多少米?
解题思路    (1)设原计划每天改造管网x米,则由题中的信息得:
(2)设以后每天改造管网还要增加m米,根据总工期不超过40天建立不等式求出其解即可.
解析    (1)设原计划每天改造管网x米,则实际施工时每天改造管网(1+20%)x米,由题意得 - =10,解得x=60,经检验,x=60是原方程的解,且符合题意.60×(1+20%)=72(米).答:实际施工时,每天改造管网的长度是72米.(2)设以后每天改造管网还要增加m米,由题意得(40-20)(72+m)≥3 600-72×20,解得m≥36.
答:以后每天改造管网至少还要增加36米.
方法归纳　在列分式方程之前,应先弄清问题中的已知量与未知量,以及它们之间的数量关系,用 含未知数的式子表示相关量,然后用题中的相等关系列出方程.求出解后,必须进行检验,既要检验 是不是所列分式方程的解,又要检验是否符合题意.
变式3(2022辽宁锦州)2022年3月23日“天宫课堂”第二课在中国空间站开讲了,精彩的直播激发 了学生探索科学奥秘的兴趣.某中学为满足学生的需求,充实物理兴趣小组的实验项目,决定购 入A、B两款物理实验套装,其中A款套装单价是B款套装单价的1.2倍,用9 900元购买的A款套装数 量比用7 500元购买的B款套装数量多5套.求A、B两款套装的单价分别是多少元.
例    (本题满分10分)甲、乙两人准备整理一批新到的实验器材.甲单独整理需要40分钟完工;甲、 乙共同整理20分钟后,乙需再单独整理20分钟才能完工.(1)问乙单独整理需要多少分钟完工?(2)若乙因工作需要,他的整理时间不能超过30分钟,则甲至少整理多少分钟才能完工?
考点1　分式方程及其解法
2.(2023山东济宁)为加快公共领域充电基础设施建设,某停车场计划购买A,B两种型号的充电桩.已 知A型充电桩比B型充电桩的单价少0.3万元,且用15万元购买A型充电桩与用20万元购买B型充电 桩的数量相等.(1)A,B两种型号充电桩的单价各是多少?(2)该停车场计划共购买25个A,B型充电桩,购买总费用不超过26万元,且B型充电桩的购买数量不 少于A型充电桩购买数量的 .问:共有哪几种购买方案?哪种方案所需购买总费用最少?
解析    (1)设B型充电桩的单价为x万元,则A型充电桩的单价为(x-0.3)万元,由题意可得 = ,解得x=1.2,经检验:x=1.2是原分式方程的解,且符合题意,∴x-0.3=0.9.答:A型充电桩的单价为0.9万元,B型充电桩的单价为1.2万元.(2)设购买A型充电桩a个,则购买B型充电桩(25-a)个,由题意可得 解得 ≤a≤ ,∵a为非负整数,∴a可取14,15,16,
∴共有三种方案方案一:购买A型充电桩14个,购买B型充电桩11个,购买费用为0.9×14+1.2×11=25.8(万元)方案二:购买A型充电桩15个,购买B型充电桩10个,购买费用为0.9×15+1.2×10=25.5(万元)方案三:购买A型充电桩16个,购买B型充电桩9个,购买费用为0.9×16+1.2×9=25.2(万元)∵25.2