3.1　函数及其图象 习题精练+知识讲解 2024年河北版中考数学一轮复习课件

这是一份3.1　函数及其图象 习题精练+知识讲解 2024年河北版中考数学一轮复习课件，文件包含31函数及其图象知识讲解pptx、31函数及其图象习题精练pptx等2份课件配套教学资源，其中PPT共68页， 欢迎下载使用。
考点复习考点1　平面直角坐标系
1.各象限内点的坐标的符号特征 
2.特殊点的坐标特征(1)坐标轴上的点的坐标特征:x轴上的点①　纵坐标为0    ;y轴上的点横坐标为0;原点的坐标为(0,0).(2)象限角平分线上的点的坐标特征:第一、三象限角平分线上的点的横、纵坐标相等;第二、四象限角平分线上的点的横、纵坐标②　互为相反数    .(3)平行于x轴(或垂直于y轴)的直线上的点的纵坐标相等;平行于y轴(或垂直于x轴)的直线上的点的 横坐标相等.
3.点到坐标轴的距离点P(x,y)到x轴的距离为|y|,到y轴的距离为③　|x|    ,到坐标原点的距离为 .
易错提醒    (1)已知点的坐标可以求出点到x轴、y轴的距离,应注意取相应坐标的绝对值.(2)已知点到x轴、y轴的距离可以求出点的坐标,但要注意分类讨论.
4.平面直角坐标系内点的对称和平移(1)点P(x,y)关于x轴对称的点的坐标为(x,-y),点P(x,y)关于y轴对称的点的坐标为④    (-x,y)    ,点P(x, y)关于原点对称的点的坐标为(-x,-y).(2)将点P(x,y)向右(或向左)平移a(a>0)个单位,得到对应点P'(x+a,y)(或(x-a,y));将点P(x,y)向上(或向下)平移b(b>0)个单位,得到对应点P'(x,y+b)(或(x,y-b)).
1.已知坐标平面上一点A,点A到x轴的距离为3,到y轴的距离恰为到x轴距离的3倍.若点A在第二象 限,则点A的坐标为 (    A    )A.(-9,3)　    B.(-3,1)C.(-3,9)　    D.(-1,3)
2.若线段AB平行于x轴,AB的长为5,且点A的坐标为(4,5),则点B的坐标为    (-1,5)或(9,5)    .
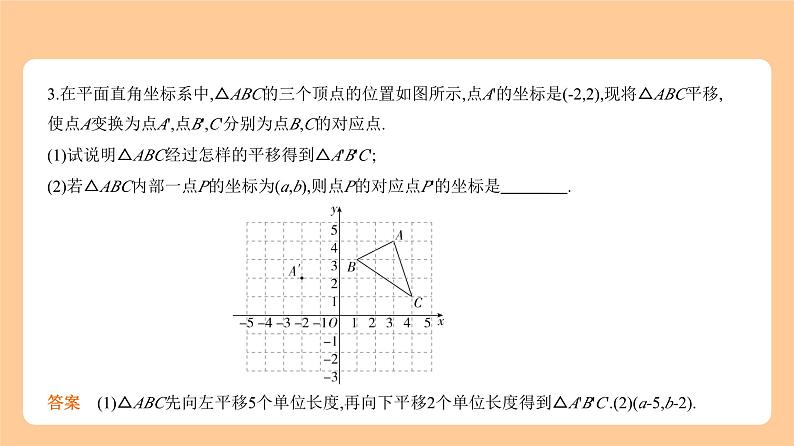
3.在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2),现将△ABC平移, 使点A变换为点A',点B',C'分别为点B,C的对应点.(1)试说明△ABC经过怎样的平移得到△A'B'C';(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P'的坐标是　　　    . 
答案    (1)△ABC先向左平移5个单位长度,再向下平移2个单位长度得到△A'B'C'.(2)(a-5,b-2).
考点2　函数及自变量的取值范围
1.函数的定义一般地,在某一变化过程中,如果有两个⑤　变量    x与y,并且对于x在某一范围内的每一个值,y都 有⑥　唯一确定    的值与它对应,那么就说y是x的函数,其中x是自变量.
2.函数自变量的取值范围是指使函数有意义的自变量的全体.求自变量的取值范围通常从两个方 面考虑:一是要使函数的解析式有意义;二是要符合实际意义.
4.水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的 是 (    C    )A.2是变量　　　　    B.π是变量C.r是变量　     D.C是常量
5.求下列函数中自变量x的取值范围.(1)y=3x-2;(2)y= ;(3)y= ;(4)y= + .
答案    (1)全体实数.    (2)x≠1.(3)x≥-3.    (4)3≤x≤5.
考点3　函数图象及其应用
1.画函数图象的步骤列表、⑦　描点    、连线.
2.函数图象上的点的坐标与其解析式之间的关系 (1)判断点是否在函数图象上的方法是将这个点的坐标代入函数解析式,若满足函数解析式,则这 个点就在该函数的图象上.(2)两个函数图象的交点坐标就是这两个函数解析式所组成的方程组的解.
注意事项　结合函数图象解决实际问题应注意以下几点:(1)横轴与纵轴所表示的变量的实际意义;(2)各个变量的取值范围;(3)函数图象的拐点的意义;(4)函数图象的变化趋势的实际意义.
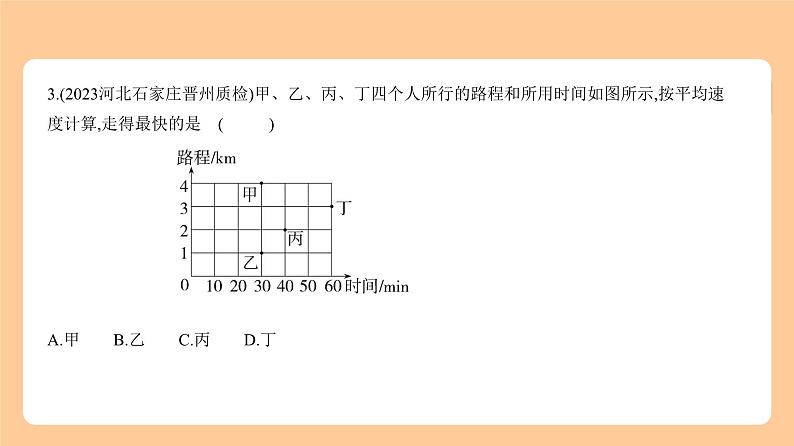
6.在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙车先出发,图中的折线段表示甲、乙两车 之间的距离y(千米)与行驶时间x(时)的函数关系,则下列说法错误的是 (    D    )A.乙车先出发0.5小时B.甲车的速度是80千米/时
一、利用函数图象正确描述实际问题的方法例1    (2021黑龙江齐齐哈尔)某人驾车匀速从甲地前往乙地,中途停车休息了一段时间,出发时油 箱中有40升油,到乙地后发现油箱中还剩4升油,则油箱中所剩油y(升)与时间t(时)之间的函数图象 大致是 (　    )
答案    C解题思路     
解析    驾车匀速从甲地前往乙地,单位时间内油箱中油的减少量是相同的,中途停车休息时油箱内 剩余油量不变,选项C中的函数图象符合题意.故选C.
方法归纳　根据实际问题分析函数图象是否正确的方法:(1)根据题目的文字信息确定函数的自变量与因变量;(2)观察函数图象时应注意横轴与纵轴所表示的量的意义;(3)要注意函数图象:①起始点和终点的位置;②转折点的位置与图象的变化趋势.
变式1 (2022北京)下面的三个问题都有两个变量:①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是 (    A    ) A.①②　    B.①③　    C.②③　    D.①②③
解析　①A、B两地的路程一定,由于汽车是匀速行驶的,所以汽车在单位时间内走的路程是相同 的,所以汽车的剩余路程y与行驶时间x是一次函数关系,故①对;②由于水箱中原有的水量是固定的,而水箱中的水是匀速放出,所以在单位时间内水的减少量是相 同的,所以水箱中的剩余水量y与放水时间x是一次函数关系,故②对;③设矩形的周长为C,则由题意可知C是定值,所以矩形中与长为x的边相邻的边长为 ,所以y=x· =-x2+ x,故y是关于x的二次函数,所以其对应的图象是抛物线,故③错.故选A.
解析    由题意可知线段表示慢车,折线表示快车,快车比慢车晚走2 h且往返花了6-2=4(h),∴v快车= = (km/h),v慢车=  km/h.设两车第一次相遇的时刻为t1,则 ·t1= ·(t1-2),解得t1=3.设两车第二次相遇的时刻为t2,则 t2+ (t2-2)=2a,解得t2= ,∴间隔时间为t2-t1= -3= (h).故选B.
题型解读　利用函数图象解决实际问题,需要从抽象的函数图象中找出关键信息,然后根据实际情 况进行计算或列方程得出结果,同时还应明确每条线段或直线所代表的实际含义,注意拐点的位置 及图象的变化趋势所反映的实际意义.
变式2 一题多问船只A出海捕鱼,一段时间后船只B追赶船只A,如图,l1,l2分别表示两船到海岸的距离 s(n mile)与追赶时间t(min)之间的关系. 根据图象回答下列问题:(1)哪条线表示B到海岸的距离与追赶时间之间的关系?(2)A,B哪个速度快?
(3)15 min内B能否追上A?(4)如果一直追下去,那么B能否追上A?(5)当A距离海岸12 n mile时,B将被迫返回.照此速度,B能否在距离海岸12 n mile前追上A?(6)l1与l2分别表示一次函数y=k1x+b1与y=k2x+b2的图象,其中k1,k2的实际意义各是什么?A与B的速度 各是多少?
解析    (1)由题意可知,当t=0 min时,B距离海岸0 n mile,即sB=0 n mile,故l1表示B到海岸的距离与追 赶时间之间的关系.(2)由题图可知,10 min内,A行驶了2 n mile,B行驶了5 n mile,所以B的速度快.(3)由(2)知,A的速度是0.2 n mile/min,B的速度是0.5 n mile/min.当t=15 min时,sA=5+15×0.2=8(n mile),sB=15×0.5=7.5(n mile).∵7.5