6.3　图形的相似 习题精练+知识讲解 2024年河北版中考数学一轮复习课件

这是一份6.3　图形的相似 习题精练+知识讲解 2024年河北版中考数学一轮复习课件，文件包含63图形的相似习题精练pptx、63图形的相似知识讲解pptx等2份课件配套教学资源，其中PPT共120页， 欢迎下载使用。
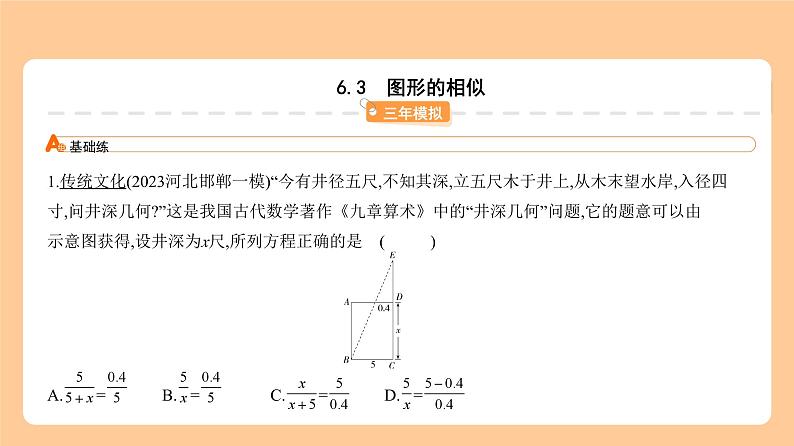
解析　如图,设AD交BE于K. ∵AD∥BC,∴△EKD∽△EBC,∴ = ,∴ = ,故选A.
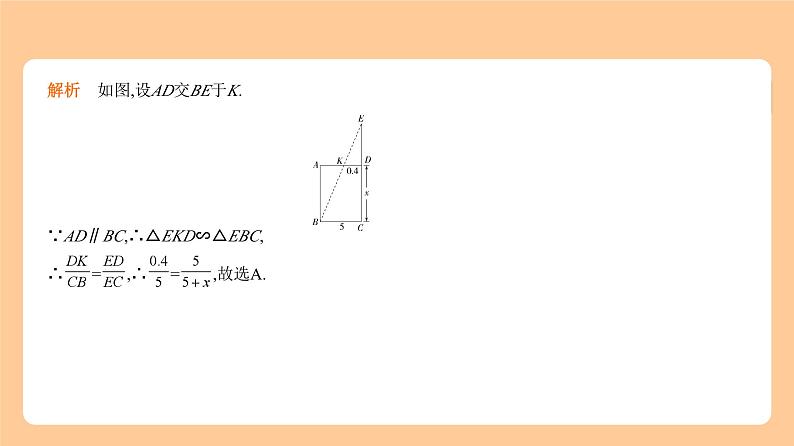
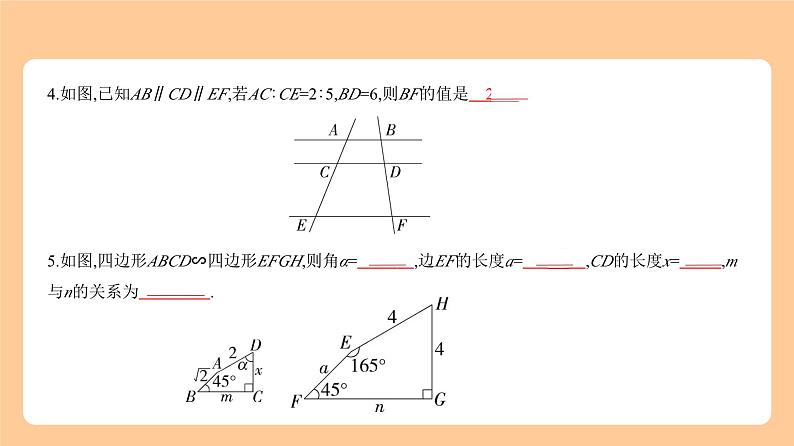
2.(2023河北邢台一模)如图,在四边形ABCD中,∠ADC=∠BAC,添加下列条件后,不能判定△ADC 和△BAC相似的是 (    C    ) A.CA平分∠BCD　    B.∠DAC=∠ABCC. = 　    D. = 
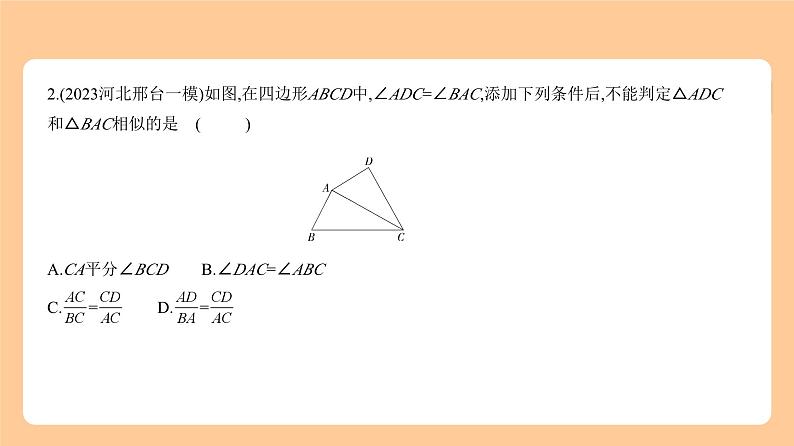
3.(2023河北邢台一模)如图,在平面直角坐标系中,△ABC与△FED关于原点O位似,且OB=2OE,若S △ABC=4,则S△FED为 (    A    ) A.1　    B.2　    C. 　    D. 
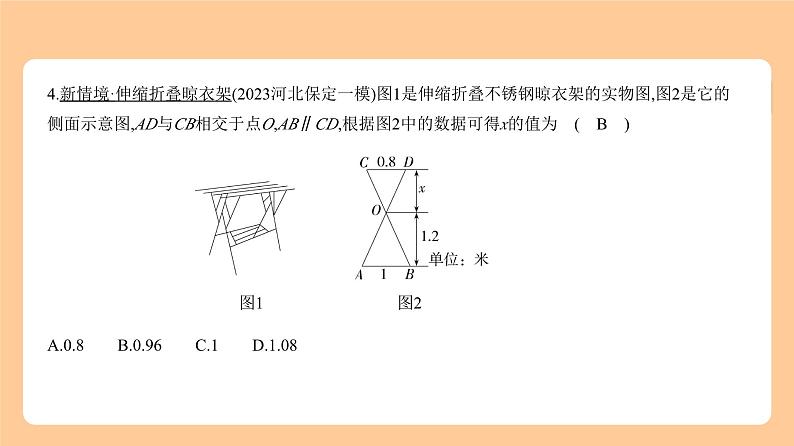
4.新情境·伸缩折叠晾衣架(2023河北保定一模)图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的 侧面示意图,AD与CB相交于点O,AB∥CD,根据图2中的数据可得x的值为 (    B    )  图1 图2  
A.0.8　    　    C.1　    
解析    ∵AB∥CD,∴△COD∽△BOA,由相似三角形对应高的比等于相似比,得 = ,∴ = ,∴x=0.96.故选B.
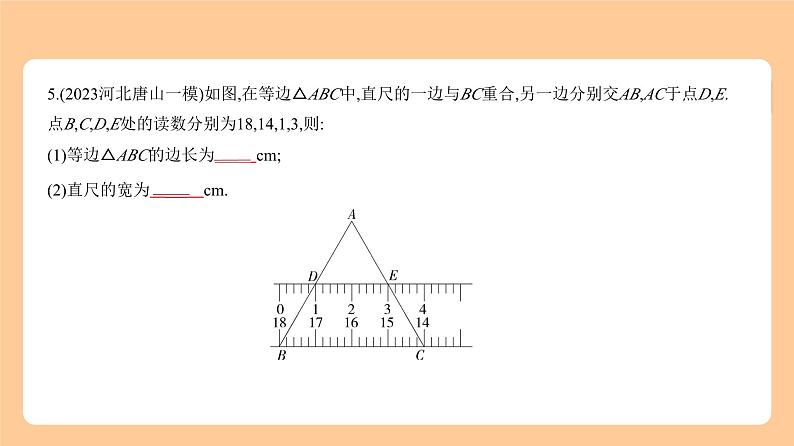
5.(2023河北唐山一模)如图,在等边△ABC中,直尺的一边与BC重合,另一边分别交AB,AC于点D,E. 点B,C,D,E处的读数分别为18,14,1,3,则:(1)等边△ABC的边长为    4    cm;(2)直尺的宽为         cm. 
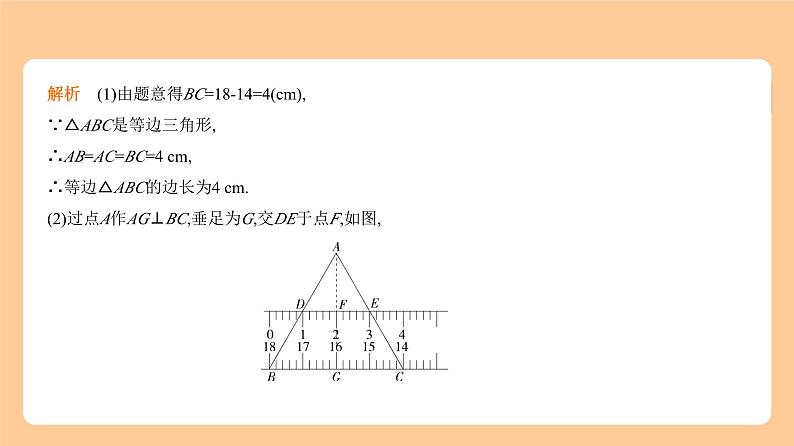
解析    (1)由题意得BC=18-14=4(cm),∵△ABC是等边三角形,∴AB=AC=BC=4 cm,∴等边△ABC的边长为4 cm.(2)过点A作AG⊥BC,垂足为G,交DE于点F,如图, 
∵△ABC是等边三角形,AG⊥BC,∴BG= BC=2 cm,∵AB=4 cm,∴AG= =2  cm,由题意得DE=3-1=2(cm),DE∥BC,∴△ADE∽△ABC,∴ = ,∴ = ,∴AF=  cm,∴FG=AG-AF=  cm,∴直尺的宽为  cm.
6.(2023河北衡水模拟)将边长为2的正六边形按照如图所示的方式向外扩张,得到新的六边形,它们 的对应边的距离均为 .(1)新的六边形与原六边形　相似    ;(填“相似”或“不相似”)(2)扩张后六边形的周长比原来增加了    12    . 
解析    (1)∵新的六边形与原六边形的对应角相等,对应边成比例,∴新的六边形与原六边形相似.(2)如图,A1B1是AB的对应边,点O为正六边形的中心,则点A在OA1上,点B在OB1上,过O点作OH1⊥A1B 1交AB于点H,则HH1= ,∵AB=2,∠AOB=60°,∴∠AOH=30°,AH=BH=1,∴OH= AH= ,∴OH=HH1,∵AB∥A1B1,∴ = = ,∴A1B1=2AB=4,
∴A1B1-AB=2,即扩张后六边形的边长比原来的边长增加了2,∴扩张后六边形的周长比原来增加了12. 
7.(2023河北石家庄模拟)如图,某校宣传栏BC后面12米处种有一排与宣传栏平行的树,即BC∥ED, 且相邻两棵树的间隔为2米,一人站在宣传栏前面的A处正好看到两端的树干,其余的树均被宣传 栏挡住.已知AF⊥BC,AF=3米,BC=10米,求该宣传栏后DE处共有多少棵树.(不计宣传栏的厚度) 
解析　延长AF交DE于点G,如图,∵AF⊥BC,BC∥ED,∴AG⊥DE,△ABC∽△ADE,∴ = ,又BC=10米,AF=3米,FG=12米,∴AG=AF+FG=15米,即 = ,∴DE=50米,50÷2+1=26(棵).答:DE处共有26棵树.
8.(2023河北秦皇岛一模)如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°, △DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E在线段BC上方旋转,在旋转过程中, 线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.  图1 图2
(1)如图1,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图2,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ.
解析    (1)证明:∵△ABC是等腰直角三角形,∴∠B=∠C=45°,AB=AC.∵AP=AQ,∴BP=CQ.∵E是BC的中点,∴BE=CE.在△BPE和△CQE中, ∴△BPE≌△CQE(SAS).(2)∵∠BEF=∠C+∠CQE=∠BEP+∠DEF,且∠C=∠DEF=45°,∴∠BEP=∠CQE,又∵∠B=∠C, ∴△BPE∽△CEQ.
1.(2023河北石家庄模拟)如图,若△ABC与△A1B1C1是位似图形,则位似中心的坐标为     (    D    ) A.(1,0)　    B.(0,1)C.(-1,0)　    D.(0,-1)
解析　如图所示,位似中心的坐标为(0,-1).故选D. 
2.(2023河北邢台一模)已知部分题干:“如图,在矩形ABCD中,AB=9,BC=15,P,Q分别是BC,CD上的 点.”张老师要求添加条件后,编写一道题目,并解决.甲、乙两人的做法如下.甲:若CQ=4,则在BC上存在2个点P,使△ABP与△PCQ相似;乙:若AP⊥PQ,则CQ的最大值为 .下列判断正确的是 (    B    ) A.甲对乙错　    B.甲错乙对C.甲、乙都对　    D.甲、乙都错
解析　甲:∵△ABP与△PCQ相似,∠B=∠C=90°,∴分两种情况求解:①当△ABP∽△PCQ时,设BP=x,则PC=15-x,∴ = ,即 = ,解得x=3或x=12.②当△ABP∽△QCP时,设BP=x,则PC=15-x,∴ = ,即 = ,解得x= .综上所述,当CQ=4时,在BC上存在3个点P,使△ABP与△PCQ相似,故甲错误.
乙:∵AP⊥PQ,∴∠APQ=90°,∴∠APB+∠CPQ=90°,又∵∠APB+∠BAP=90°,∴∠BAP=∠CPQ,∴△ABP∽△PCQ,∴ = ,设BP=x,则PC=15-x,即 = ,∴CQ= x(15-x)=-  + .∵- 16,所以甲、乙方案均错误,周长和的最大值错误.故选D.
4.传统文化(2022陕西中考)在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种 “优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法所作的EF将矩形ABCD分 为上下两部分,其中E为边AB的黄金分割点,即BE2=AE·AB.已知AB为2米,则线段BE的长为    ( -1)  米. 
解析    设BE为x米,则AE=AB-BE=(2-x)米,所以x2=2(2-x),解得x= -1或x=- -1(舍去).故线段BE的长为( -1)米.
5.(2023河北邢台一模)如图,在平行四边形ABCD中,对角线AC,BD交于点O.过点O作BD的垂线,交 BA的延长线于点E,交AD于点F,交BC于点N.若EF=OF,∠CBD=30°,BD=6 ,则:(1) =         ;(2)AF的长为    2    . 
解析    (1)∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,∴∠FAO=∠NCO.在△AFO和△CNO中, ∴△AFO≌△CNO(ASA),∴FO=NO,∵EF=OF,∴EF=OF=ON,∴ = .
(2)∵AF∥BC,∴△EAF∽△EBN,∴ = = .∵四边形ABCD是平行四边形,∴BO=OD= BD=3 ,NO⊥BO.∵∠CBD=30°,∴cs∠CBD= = = ,∴BN=6,∴ = ,∴AF=2.
6.(2023河北唐山模拟)如图,在Rt△ABC中,∠ACB=90°,M是斜边AB的中点,MD∥BC,且MD=CM,DE ⊥AB于点E,连接AD,BD.(1)求证:△MED∽△BCA;(2)当S△BDM= S△ABC时,求S△BED∶S△MED的值;(3)在(2)的条件下,求cs∠ABC的值. 
解析    (1)证明:∵MD∥BC,∴∠DME=∠ABC,∵∠MED=∠BCA=90°,∴△MED∽△BCA.(2)∵∠ACB=90°,点M是斜边AB的中点,∴MB=MC=AM= AB,∵MC=MD,∴MD= AB,∵△MED∽△BCA,∴ = = ,
又∵S△BDM= S△ABC,∴ = ,∴S△BED∶S△MED=1∶3.(3)∵ = ,∴ = ,∵MD=MB,∴ = ,∴cs∠DME= = ,又∵∠DME=∠ABC,∴cs∠ABC= .
7.(2022河北唐山二模)如图,在矩形ABCD中,AB=6,AD=8,把AB绕点B顺时针旋转α(0°