






初中浙教版5.3 一次函数精品课件ppt
展开会用待定系数法求一次函数的表达式.
通过实例进一步加深对一次函数的认识.
会用一次函数解决简单的实际问题.
1. 一次函数的概念是什么?
2. 正比例函数的概念是什么?
一般地,函数y=kx+b(k、b都是常数,且k≠0 ) 叫做一次函数 (x为自变量,y为函数值).
当b=0时,一次函数y=kx+b就成为y=kx( k为常数,k≠0),叫做正比例函数.
3. 已知y是x的正比例函数,当x=-2时,y=8. 求y与x之间的函数关系式.
确定正比例函数表达式只需求哪个值?
解:设正比例函数关系式是 y=kx, 把x=-2,y=8代入上式,得8=-2k, 解得 k=-4, 所求的正比例函数关系式是 y=-4x .
那确定一次函数表达式要求哪些值呢?
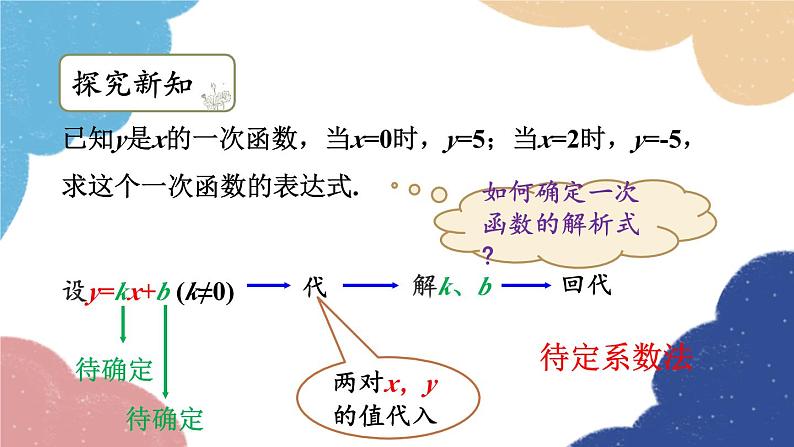
已知y是x的一次函数,当x=0时,y=5;当x=2时,y=-5,求这个一次函数的表达式.
如何确定一次函数的解析式?
设y=kx+b (k≠0)
解:因为y是x的一次函数,所以设所求表达式为y=kx+b(k≠0).将x=0时,y=5和x=2,y=-5分别代入上式,得:
所以,所求的一次函数表达式为y=-5x+5.
你能总结用待定系数法求函数解析式的一般步骤吗?
(1)设:设所求一次函数表达式为y=kx+b(k≠0),其中k 、b是待确定的常数,k≠0 .(2)代:把两对已知的自变量与函数的对应值分别代入y=kx+b,得到关于k、b的二元一次方程组. (3)求:解这个关于k 、b的二元一次方程组,求出k 、b的值. (4)写:把求得的k 、b的值代入y=kx+b,就得到所求的一次函数表达式.这种求函数表达式的方法叫做待定系数法.
例1 已知一次函数y=kx+b,当x=0时,y=1;当x=1时,y=0. 试确定这个函数的表达式.
分析:分别将x=0,y=1和x=1,y=0代入y=kx+b中,得到关于k、b的二元一次方程组,解之即可.
解:将x=0,y=1和x=1,y=0分别代入y=kx+b, 得 所以这个函数的表达式为y=-x+1.
例2 一辆汽车匀速行驶,当行驶了 20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油y(L)与汽车行驶的路程x(km)之间是一次函数关系,请求出这个一次函数的表达式, 并写出自变量x的取值范围以及常数项的意义.
分析:(1)确认其为一次函数.(2)设表达式为y=kx+b.(3)根据变量的两组对应值列方程组,求出k、b的值.
解:设所求一次函数的表达式为y=kx+b. 根据题意,把已知的两组对应值(20,58. 4)和(50,56)代入 y=kx+b,得所以这个一次函数表达式为y=-0.08x+60.因为剩余油量y≥0,所以-0.08x+60 ≥0. 解得x≤750.因为路程x≥0,所以0≤x≤750.因为当x=0时,y=60,所以这辆汽车行驶前油箱存油60 L.
1.已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的表达式为( )A.y=2x B.y=-2x C.y=- x D.y=-x
2. 若一次函数y=kx+b的图象经过点(0,2)和(1,0),则这个函数的表达式是( )A.y=2x+3 B.y=3x+2C.y=x+2 D.y=-2x+2
3. 已知y+2与x-1成正比例,且当x=3时,y=4.(1)求y与x之间的函数表达式;(2)当y=1时,求x的值.
解:(1)设y+2=k(x-1)(k≠0), 把x=3,y=4代入,得4+2=k(3-1),解得k=3. 则y与x之间的函数表达式是y+2=3(x-1), 即y=3x-5. (2)当y=1时,3x-5=1,解得x=2.
4.某市举办一场中学生羽毛球比赛.场地和耗材需要一些费用.其中场地费b(元)是固定不变的,耗材费用与参赛人数x(人)成正比例函数关系,这两部分的总费用为y(元).已知当x=20时,y=1 600;当x=30时,y=2 000.(1)求y与x之间的函数关系式.
解:(1)设y与x之间的函数关系式为y=kx+b, 因为当x=20时,y=1 600;当x=30时,y=2 000, 所以 所以y=40x+800(x为正整数).
4.某市举办一场中学生羽毛球比赛.场地和耗材需要一些费用.其中场地费b(元)是固定不变的,耗材费用与参赛人数x(人)成正比例函数关系,这两部分的总费用为y(元).已知当x=20时,y=1 600;当x=30时,y=2 000.(1)求y与x之间的函数关系式.(2)当支出总费用为 3 200元时,有多少人参加了比赛?
解:当y=3 200时,40x+800=3 200,解得x=60. 所以当支出总费用为3 200元时,有60人参加了比赛.
用待定系数法求一次函数表达式要明确两点:(1)具备条件:一次函数y=kx+b中有两个不确定的系数k、b,需要两个独立的条件确定两个关于k、b的方程,联立方程,解方程组求得k,b的值.这两个条件通常是两个点的坐标或两对x,y的值.(2)确定方法:将两对已知变量的对应值分别代入y=kx+b中,建立关于k、b的方程组,通过解这个方程组求出k、b,从而确定其表达式.
初中浙教版5.3 一次函数备课课件ppt: 这是一份初中浙教版5.3 一次函数备课课件ppt,共20页。PPT课件主要包含了l2πr,y50+12x,T5-2t,m78V,小试牛刀,函数是正比例函数,∴m-1,变式训练,∴m-2,-4k等内容,欢迎下载使用。
初中数学沪科版八年级上册12.2 一次函数习题ppt课件: 这是一份初中数学沪科版八年级上册12.2 一次函数习题ppt课件,共22页。PPT课件主要包含了关于kb的方程组,待定系数法,y=x-1,y=2x+2,-3x+4等内容,欢迎下载使用。
数学八年级上册第5章 一次函数5.3 一次函数示范课课件ppt: 这是一份数学八年级上册第5章 一次函数5.3 一次函数示范课课件ppt,共23页。PPT课件主要包含了教学目标,y=5x,y=6x,y=kx,y=kx+b,待确定,解一元一次方程,解二元一次方程组,正比例函数,一次函数等内容,欢迎下载使用。













