江苏省南京市江宁区南京市竹山中学2023-2024学年八年级下学期3月月考数学试题

这是一份江苏省南京市江宁区南京市竹山中学2023-2024学年八年级下学期3月月考数学试题，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

总分: 100分 时间: 100 分钟
一、单选题(本大题共6小题，每小题2分，共12分.)
1.下列图形既是中心对称图形，又是轴对称图形的是( )
A. 直角三角形 B. 等腰三角形 C. 平行四边形 D. 菱形
2.下列调查中，不适合采用普查的是( )
A. 某航空公司检测80家民航客机的安全性能B.检测某城市的空气质量状况
C. 对全校同学进行每日温度测量统计 D. 调查某中学教师的身体健康状况
3.为了了解我校八年级 1500名学生的跳绳成绩，体育老师从中抽查150名学生的跳绳成绩进行统计分析，下列说法正确的是( )
A. 每名学生是个体 B. 被抽取的150名学生是样本
C. 150是样本容量 D. 1500名学生是总体
4.下列命题中，错误的是( )
A. 两条对角线相等的平行四边形是矩形 B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直的矩形是正方形 D. 两条对角线互相平分的四边形是平行四边形
5. 如图, 点E 是▱ABCD 边 AD延长线上一点,连接BE、 CE、BD, BE 与CD交于点 F . 添加以下条件，不能判定四边形BCED为平行四边形的是( )
A. DE =DA B. ∠ABD=∠DCE C. ∠DEB=∠BCD D. EF=FB
6. 如图, 在一张矩形纸片 ABCD中, AB=4, BC=8, 点E, F 分别在AD, BC上, 将矩形ABCD沿直线EF 折叠，点C落在AD上的一点 H处，点D落在点G处，有以下四个结论：
①四边形CFHE 是菱形; ②EC平分∠DCH; ③线段 BF₁的取值范围为3≤BF≤4;④当H与点A重合时， EF=25.其中正确的结论是( )
A.①②③④ B. ①④ C. ①②④ D. ①③④
试卷第1页，共6页二、填空题(本大题共10小题，每小题2分，共20分.)
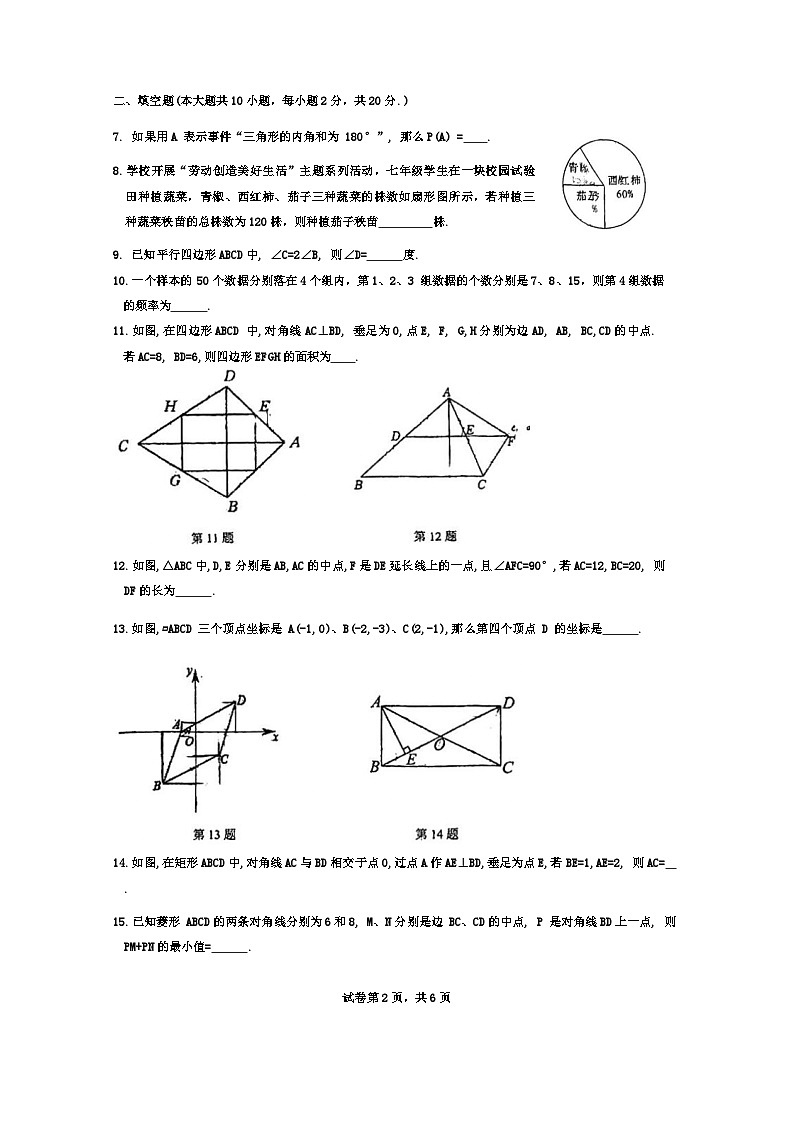
7. 如果用A 表示事件“三角形的内角和为 180°”, 那么P(A) = .
8.学校开展“劳动创造美好生活”主题系列活动，七年级学生在一块校园试验田种植蔬菜，青椒、西红柿、茄子三种蔬菜的株数如扇形图所示，若种植三种蔬菜秧苗的总株数为120株，则种植茄子秧苗 株.
9. 已知平行四边形ABCD中, ∠C=2∠B, 则∠D= 度.
10.一个样本的 50个数据分别落在4个组内，第1、2、3 组数据的个数分别是7、8、15，则第4组数据的频率为 .
11.如图,在四边形ABCD 中,对角线AC⊥BD, 垂足为O,点E, F, G,H分别为边AD, AB, BC,CD的中点.若AC=8, BD=6,则四边形EFGH的面积为 .
12.如图,△ABC中,D,E分别是AB,AC的中点,F是DE延长线上的一点,且∠AFC=90°,若AC=12,BC=20, 则DF的长为 .
13.如图,▱ABCD 三个顶点坐标是 A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点 D 的坐标是 .
14.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若BE=1,AE=2, 则AC= .
15.已知菱形 ABCD的两条对角线分别为6和8, M、N分别是边 BC、CD的中点, P 是对角线BD上一点, 则PM+PN的最小值= .
试卷第2页，共6页
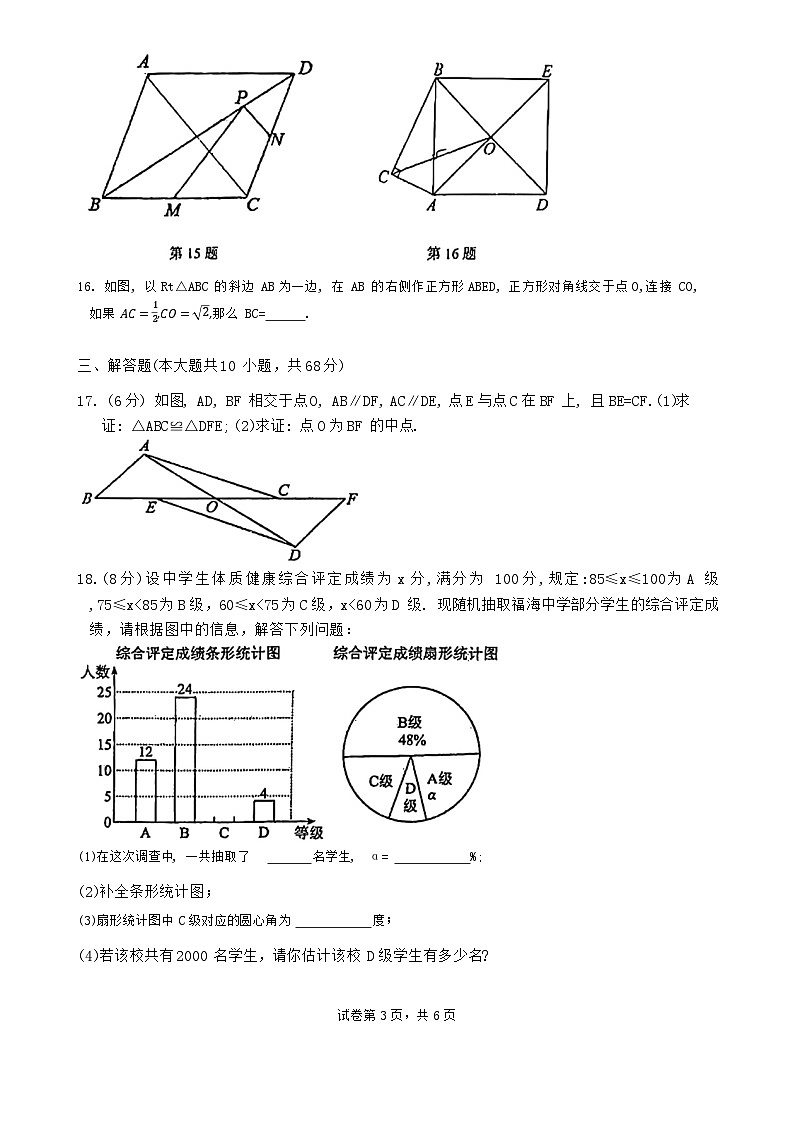
16. 如图, 以Rt△ABC 的斜边 AB为一边, 在 AB 的右侧作正方形ABED, 正方形对角线交于点O,连接 CO, 如果 AC=12,CO=2,那么 BC= .
三、解答题(本大题共10 小题，共68分)
17. (6分) 如图, AD, BF 相交于点O, AB∥DF, AC∥DE, 点E与点C在BF 上, 且BE=CF.(1)求证: △ABC≌△DFE; (2)求证: 点O为BF 的中点.
18.(8分)设中学生体质健康综合评定成绩为x分,满分为 100分,规定:85≤x≤100为A 级,75≤x<85为B级，60≤x<75为C级，x<60为D 级. 现随机抽取福海中学部分学生的综合评定成绩，请根据图中的信息，解答下列问题：
(1)在这次调查中, 一共抽取了 名学生, α= %;
(2)补全条形统计图；
(3)扇形统计图中 C级对应的圆心角为 度；
(4)若该校共有2000 名学生，请你估计该校 D级学生有多少名?
试卷第3页，共6页19.(6分) 某市林业局积极响应习总书记“青山绿水就是金山银山”的号召，特地考察一种花卉移植的成活率，对本市这种花卉移植成活的情况进行了调查统计，并绘制了如图所示的统计图.
请你根据统计图提供的信息，回答下列问题：
(1)估计这种花卉成活概率为 . (精确到0.1)
(2)该林业局已经移植这种花卉20000 棵.
①估计这批花卉成活的棵树；
②根据市政规划共需要成活90000 棵这种花卉，估计还需要移植多少棵?
20.(6分)如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上.
(1)将△ABC向左平移6个单位长度得到△A₁B₁C₁,请画出△A₁B₁C₁:
(2)画出△A₁B₁C₁关于点O的中心对称图形△A₂B₂C₂;
(3)若将△ABC绕某一点旋转可得到△A₂B₂C₂，那么旋转中心的坐标是————·
21.(6分) 如图，A是直线l外一点，分别按下列要求作图.
(1)在图①中作正方形ABCD,使得点 B, D在l上;
(2)在图②中作菱形ABCD,使得点B, D在l上,且∠ABC=60°.
(要求：用直尺和圆规作图，保留作图痕迹，写出必要的文字说明)
试卷第4页，共6页22. (7分)如图,在四边形ABCD中, AB‖DC,AB=AD,,对角线AC,BD交于点O, AC平分. ∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1) 求证: 四边形ABCD是菱形;
(2) 若 AB=5,BD=2, 求OE的长.
23.(6分) 对“中位线定理”逆向思考，可得命题：在三角形内，经过三角形一边中点，且与另一边平行的线段，是三角形的中位线.这是一个真命题，填空并证明.
如图: 已知D是AB的中点, ,求证: .
24. (7分) 如图, 四边形AECF 是菱形, 对角线AC、 EF 交于点O, 点 D、 B 是对角线EF 所在直线上两点, 且DE=BF, 连接AD、 AB、 CD、 CB, ∠ADO=45°.
(1)求证: 四边形 ABCD是正方形: (2)若正方形ABCD的面积为32, BF=1, 求点 F到线段AE的距离.
25.(7分) 如图, 将矩形ABCD绕着点C按顺时针方向旋转得到矩形 FECG, 点 B 与点E对应, 点E恰好落在AD边上, BH⊥CE交于点H.
(1)求证: AB=BH;
(2)连接BG交 CH于O, 已知. AB=5,BC=13,求BO的长.
试卷第5页，共6页26.(9分) 定义：有一组对边相等且这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”.
(1)如图①,四边形ABCD 与四边形AEFG 都是正方形, 135°<∠AEB<180°,求证:四边形BEGD 是“等垂四边形”：
(2)如图②, 四边形ABCD是“等垂四边形”. AD*BC,连接BD, 点E, F, G分别是AD, BD, BC的中点, 连接 EG, FG, EF. 试判定 △EFG的形状，并证明你的结论：
(3)如图③, 四边形ABCD 是“等垂四边形”. . AD=6,BC=10,请直接写出边 AB长的最小值.
试卷第6页，共6页