2023年吉林省松原市宁江区三校九年级中考第三次模拟数学模拟试题

这是一份2023年吉林省松原市宁江区三校九年级中考第三次模拟数学模拟试题，共16页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
一、单项选择题（每小题2分，共12分）
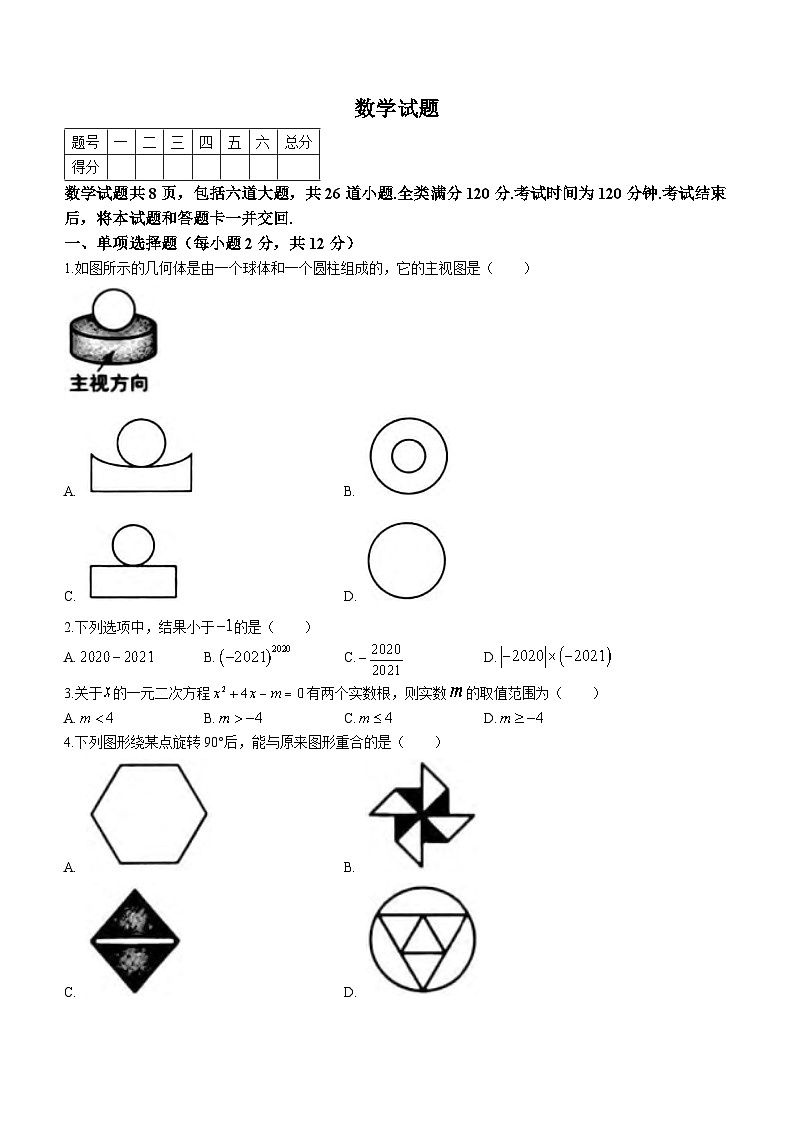
1.如图所示的几何体是由一个球体和一个圆柱组成的，它的主视图是（ ）
A. B.
C. D.
2.下列选项中，结果小于的是（ ）
A.B.C.D.
3.关于的一元二次方程有两个实数根，则实数的取值范围为（ ）
A.B.C.D.
4.下列图形绕某点旋转90°后，能与原来图形重合的是（ ）
A. B.
C. D.
5.如图，是的直径，点，在上.若.则的大小是（ ）
A.130°B.120°C.110°D.100°
6.如图，已知，点为边上一点，，点为线段的中点，以点为圆心，线段长为半径作弧，交于点，连接，则的长是（ ）
A.5B.C.D.
二、填空题（每小题3分，共24分）
7.计算：______.
8.不等式的解集是______.
9.化简的结果是______.
10.一副三角板如图摆放，若，则的度数为______°.
11.如图，，分别是的边，的中点，若的面积为1，则四边形的面积等于______.
12.如图，用一个半径为的定滑轮带动重物上升，滑轮上一点旋转了36°，假设绳索（粗细不计）与滑轮之间没有滑动，则重物上升了______.
13.如图，每个小长方形的长为，宽为，则四边形的面积为______.
14.小英用一张直角三角形纸片玩折纸游戏，如图所示，在中，，，.点在斜边上，连接，将沿折叠，点的对应点落在边上，则折叠后纸片重叠阴影部分的面积为______.
三、解答题（每小题5分，共20分）
15.先化简，再求值：，其中.
16.已知：如图所示，，点为线段上一点，连接交于点，过点作分别交，于点，点，，求证：.
17.王师傅开车带着儿子去参观我省举办的“喜迎二十大・奋进新征程——乡村振兴成果展”，他的车前有两辆车即将行驶到有信号灯的路口，该路口的信号灯分别为：直行、左转和右转.王师傅给儿子提出下列两个问题，请你帮助王师傅的儿子解答：
（1）在我们车前面的第一辆车直行的概率是______；
（2）用画树状图（或列表）的方法，求在我们车前面的两辆车向同一个方向行驶的概率.
18.盲盒顾名思义就是盒子中放置不同的物品，消费者凭运气抽中商品，正是这种随机化的体验，让消费者产生消费欲望，成为当下最热门的营销方法之一.某葡萄酒酒庄为回馈新老客户，也推出了盲盒式营销.商家计划在每件盲盒中放入，两种类型的酒，共6瓶.销售人员先包装了甲、乙两种盲盒.甲盲盒中装了种酒3瓶，种酒3瓶；乙盲盒中装了种酒1瓶，种酒5瓶；经过测算，甲盲盒的成本价为每件240元，乙盲盒的成本价为每件160元.
（1）种酒和种酒的成本价为每瓶多少元；
（2）商家为回馈新老客户，计划所有的盲盒售价都为每件299元，请你再直接写出一种盲盒装箱的方案（题中两种方案除外），使它的成本价不高于299元.
四、解答题（每小题7分，共28分）
19.图①，图②，图③均是的正方形网格，每个小正方形的顶点称为格点.小正方形的边长为1，点，均在格点上.在图①，图②，图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法.
图① 图② 图③
（1）在图①中，以线段为边画一个等腰三角形，且的面积为4；
（2）在图②中，以线段为边画一个轴对称四边形，且四边形的面积为10；
（3）在图③中，以线段为边画一个四边形，使，且四边形的面积为8.
20.某区为了解各学校中学生体育锻炼的情况，对甲、乙两个学校各180名学生进行了体育测试，从中各随机抽取30名学生的成绩（百分制），并对成绩（单位：分）进行整理、描述和分析.给出了部分成绩信息.
甲校参与测试的学生成绩分布如表：
甲校参与测试的学生成绩在这一组的数据是：
96，96.5，97，97.5，96.5，96.5，97.5，96，96.5，96.5
甲、乙两校参与测试的学生成绩的平均数、中位数、众数如表，根据以上信息，回答下列问题：
（1）______；
（2）在此次随机抽样测试中，甲校的王同学和乙校的李同学成绩均为97分，则在各自学校参与测试同学中成绩的名次相比较更靠前的是______（填“王”或“李”）同学，请简要说出理由；
（3）在此次随机测试中，乙校96分以上的总人数比甲校96分以上（含96分）的总人数的2倍少100人，试估计乙校96分以上（含96分）的总人数.
21.如图，已知图①是超市购物车，图②是超市购物车侧面示意图，测得支架，，，均与地面平行，支架与之间的夹角.
图① 图②
（1）求两轮轮轴，之间的距离；
（2）若的长度为，，求点到所在直线的距离.（结果精确到0.1，参考数据：，）
22.如图，是一个“函数求值机”的示意图，其中是的函数.下面表格中，是通过该“函数求值机”得到的几组与的对应值.
根据以上信息，解答下列问题：
（1）当输入的值为1时，输出的值为______；
（2）求，的值；
（3）当输出的值为0时，求输入的值.
五、解答题（每小题8分，共16分）
23.小丽家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热，此过程中水温与开机时间（分）满足一次函数关系，当加热到100℃时自动停止加热，随后水温开始下降，此过程中水温与开机时间（分）成反比例关系，当水温降至20℃时，饮水机又自动开始加热…，重复上述程序（如图所示），根据图中提供的信息，解答问题：
（1）当时，求水温与开机时间（分）的函数关系式；
（2）求图中的值；
（3）若小丽在通电开机后即外出散步，请你预测小丽散步70分钟回到家时，饮水机内的温度约为多少℃？
24.【问题情境】在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图①，将：矩形纸片沿对角线剪开，得到和.并且量得，.
【操作发现】
（1）将图①中的以点为旋转中心，按逆时针方向旋转，使，得到如图②所示的，过点作的平行线，与的延长线交于点，则四边形的形状是______；
（2）创新小组将图①中的以点为旋转中心，按逆时针方向旋转，使，，三点在同一条直线上，得到如图③所示的，连接，取的中点，连接并延长至点，使，连接，得到四边形，请你判断四边形的形状，并证明你的结论；
【实践探究】
（3）缜密小组在创新小组发现结论的基础上，进行如下操作：将沿着方向平移，使点与点重合，此时点平移至点，与相交于点，如图④所示，连接，直接写出的值.
图① 图② 图③ 图④
六、解答题（每小题10分，共20分）
25.如图①所示，在等腰直角三角形中，，，于点，点从点出发，沿方向以的速度运动到点停止，在运动过程中，过点作交于点，以线段为边作等腰直角三角形，且（点，位于异侧）.设点的运动时间为，与重跙部分的面积为.
图① 图②
（1）如图②，当点落在上时，______；
（2）求点落在上时的值；
（3）若点在下方时，求重叠部分面积与运动时间的函数表达式.
26.在平面直角坐标系中，抛物线的对称轴是直线，与轴交点的坐标为.
（1）求此抛物线对应的函数表达式；
（2）①当时，的取值范围是______；
②若时，，则的取值范围是______；
（3）当时，若函数的图象上有且只有一个点到直线的距离为1，求的取值范围；
（4）点，点均在这个抛物线上（点在点的右侧），点的横坐标为，点的横坐标为.将此抛物线上，两点之间的部分（包括，两两点）记为图象.设图象最高点的纵坐标与最低点的纵坐标的差为，求与之间的函数关系式.
参考答案
1. C 2. D 3. D 4. B 5. B 6. A
7. 8. 9. 10.105 11.3 12. 13. 14.
15.解：原式.
16.证明：∵，，
∴，.
∵，∴，即.
在和中，
.
17.解：（1）；
（2）根据题意，列表如下：（4分）
由表格可知，共有9种等可能的结果，其中，两辆车向同一方向行驶的结果有3种，分别是（直，直），（右，右）和（左，左），
∴.
18.解：（1）设种酒的成本价为每瓶元，种酒的成本价为每瓶元.
由题意，得，解得
答：种酒的成本价为每瓶60元，种酒的成本价为每瓶20元；
（2）∵，
∴盲盒中装种酒4瓶，种酒2瓶（答案不唯一）.
19.解：（1）如图①中，即为所求；
（2）如图②中，四边形即为所求；
（3）如图③中，四边形即为所求.
图① 图② 图③
20.解：（1）96.5；（2）王（3分）
理由：97分在甲校的中位数之上，在乙校的中位数之下，因此王同学在甲校的排名在前；
（3）样本中，甲校96分以上的学生人数所占的百分比为，
所以甲校96分以上的学生人数为（人）.
因此乙校96分以上的学生人数为（人）.
答：乙校96分以上（含96分）的总人数为140人.（7分）
21.解：（1）∵支架与之间的夹角为90°，
∴.
两轮轮轴，之间的距离为；
（2）过点作于，过点作延长线与，
图②
则扶手到所在直线的距离为.
∵的长度为，，
∴.
∵，∴.
∴.
∴.
由（1）知，，，
∴.
.解得.
∴.
扶手到所在直线的距离为.
22.解：（1）8；
（2）将代入，
得，解得
（3）令，由得.
∴（舍去）.
由，得.∴.
∴输出的值为0时，输入的值为.
23.解：（1）当时，设水温与开机时间（分）的函数关系为：.
依据题意，得，解得
∴此函数解析式为：；
（2）当，设水温与开机时间（分）的函数关系式为：.
依据题意，得.即.
故.
当时，，解得，
（3）∵，∴当时，.
答：小丽散步70分钟回到家时，饮水机内的水的温度约为50℃.
24.解：（1）菱形；
提示：在图①中，
∵是矩形的对角线，
∴，.
∴.
在图②中，由旋转知，，.
∴.
∵，∴
∴.
∵，∴四边形是平行四边形.
又∵，∴是㨖形；
（2）四边形是正方形；
证明：在图①中，
∵四边形是矩形，∴.
∴，.
∴
在图③中，由旋转知，，
∴.
∴.
∵点，，在同一条直线上，∴.
由旋转知，.
∵点是的中点，∴，.
∵，∴四边形是平行四边形.
∵，∴是菱形.
又∵，∴菱形是正方形；
（3）.
提示：在中，，，∴.
∴，
∴.
由（2）结合平移知，.
在中，，
∴.
∴.
在中，，
∴.
在中，.
25.解：（1）4；
提示：当点落在上时，如图①：
图①
∵，，是等腰直角三角形，
∴，.
∴四边形是正方形.∴.
∵是等腰直角三角形，∴.
∴是等腰直角三角形.∴.
∴.∴；
（2）点落在上时，如图②：
图②
∵等腰直角三角形中，，
∴，是等腰直角三角形.
∵，∴.
∵，，∴.
∵是等腰直角三角形，∴.
∴.∴.
又∵，∴.
∴.
设，则.
∴.解得.
∴.∴；
（3）ⅰ）当在下方时，如图③：
图③
∵，，∴
∴，是等腰直角三角形.
∴.∴.
∵，，
∴.∴
∵，∴
∵，，∴.∴
ⅱ）当在上方时，如图④：
图④
∵，，∴.
∴，.
在等腰直角三角形中，，
∴
∴.
综上所述，
26.解：（1）∵抛物线的对称轴是直线，与轴交点的坐标为，
∴解得
∴抛物线对应的函数表达式为；
（2）①；②；
（3）如图，在直线上方，到直线距离为1的点在直线上，在中，
令，得.
解得或.
∵当时，函数的图象上有且只有一个点到直线的距离为1，
∴，解得；
（4）当时，.
当时，.
抛物线顶点为.
∵在的右侧，∴.解得.
当，即时，.
当，且，
即时，.
当，且，
即时，.
综上所述，
题号
一
二
三
四
五
六
总分
得分
我们挑选口感口碑都不错的酒作为盲盒不管
您是自喝还是送礼都是不错的选择
在这里你可以尝到不同类型的葡萄酒
数量有限，欲购从速
好玩 有趣 神秘
成绩（分）
甲校
2
3
5
10
10
学校
平均数
中位数
众数
甲校
96.35
99
乙校
95.85
97.5
99
输入
…
0
2
…
输出
…
2
6
16
…
二
一
直
右
左
直
（直，直）
（直，右）
（直，左）
右
（右，直）
（右，右）
（右，左）
左
（左，直）
（左，右）
（左，左）