最新中考数学压轴大题之经典模型 专题11 四点共圆模型-【压轴必刷】

这是一份最新中考数学压轴大题之经典模型 专题11 四点共圆模型-【压轴必刷】，文件包含专题11四点共圆模型-压轴必刷2023年中考数学压轴大题之经典模型培优案全国通用原卷版docx、专题11四点共圆模型-压轴必刷2023年中考数学压轴大题之经典模型培优案全国通用解析版docx等2份试卷配套教学资源，其中试卷共106页， 欢迎下载使用。

今天整理了初三中考总复习阶段在教学过程中收集的经典题目，一共有31讲，包括原卷版和解析版，供大家学习复习参考。
经典题目1：这是一道非常经典的最值问题，最值模型将军饮马和一箭穿心。
经典题目2：上面三道题是费马点经典问题，旋转转化是费马点问题的关键。
经典题目3：阿氏圆经典题目，这道题目实际包括了隐圆模型，一箭穿心模型等常见几何模型。
经典题目4：这是中考出现频率比较高的胡不归问题，也是经典最值问题。
【压轴必刷】2023年中考数学压轴大题之经典模型培优案
专题11四点共圆模型
解题策略
模型1：定点定长共圆模型
若四个点到一个定点的距离相等，则这四个点共圆．如图，若OA＝OB＝OC＝OD，则A，B，C，D四点在以点O为圆心、OA为半径的圆上．
模型2：对角互补共圆模型
2．若一个四边形的一组对角互补，则这个四边形的四个顶点共圆．
如图，在四边形ABCD中， 若∠A＋∠C＝180°（或∠B＋∠D＝180°）则A，B，C，D四点在同一个圆上．

拓展：若一个四边形的外角等于它的内对角，则这个四边形的四个顶点共圆．
如图，在四边形ABCD中，∠CDE为外角，若∠B＝∠CDE，则A，B，C，D四点在同一个圆上．
模型3：定弦定角共圆模型
若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线段的两个端点共圆
如图，点A，D在线段BC的同侧，若∠A＝∠D，则A，B，C，D四点在同一个圆上．
经典例题
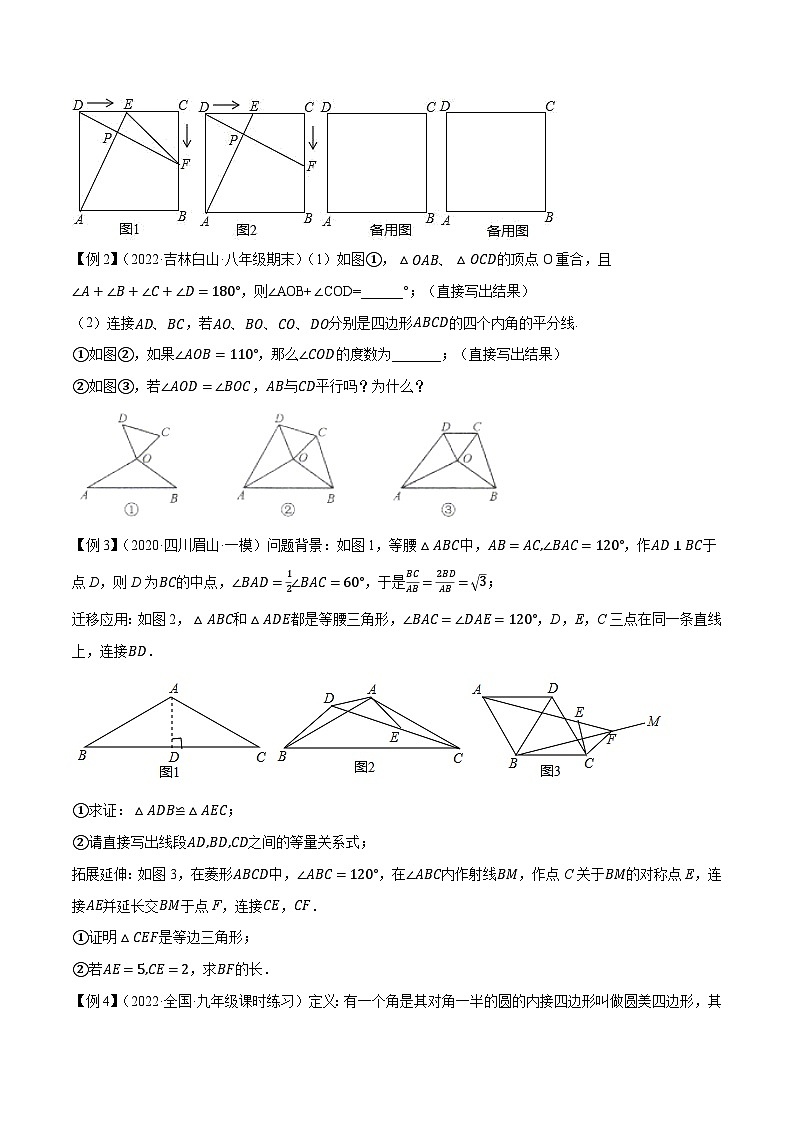
【例1】．（2021·全国·九年级课时练习）在边长为12cm的正方形ABCD中，点E从点D出发，沿边DC以1cm/s的速度向点C运动，同时，点F从点C出发，沿边CB以1cm/s的速度向点B运动，当点E达到点C时，两点同时停止运动，连接AE、DF交于点P，设点E． F运动时间为t秒．回答下列问题：
(1)如图1，当t为多少时，EF的长等于45cm?
(2)如图2，在点E、F运动过程中，
①求证：点A、B、F、P在同一个圆(⊙O)上；
②是否存在这样的t值，使得问题①中的⊙O与正方形ABCD的一边相切?若存在，求出t值；若不存在，请说明理由；
③请直接写出问题①中，圆心O的运动的路径长为_________．
【例2】（2022·吉林白山·八年级期末）（1）如图①，△OAB、△OCD的顶点O重合，且∠A+∠B+∠C+∠D=180°，则∠AOB+∠COD=______°；（直接写出结果）
（2）连接AD、BC，若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.
①如图②，如果∠AOB=110°，那么∠COD的度数为_______；（直接写出结果）
②如图③，若∠AOD=∠BOC，AB与CD平行吗？为什么？
【例3】（2020·四川眉山·一模）问题背景：如图1，等腰△ABC中，AB=AC,∠BAC=120°，作AD⊥BC于点D，则D为BC的中点，∠BAD=12∠BAC=60°，于是BCAB=2BDAB=3；
迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，D，E，C三点在同一条直线上，连接BD．
①求证：△ADB≌△AEC；
②请直接写出线段AD,BD,CD之间的等量关系式；
拓展延伸：如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF．
①证明△CEF是等边三角形；
②若AE=5,CE=2，求BF的长．
【例4】（2022·全国·九年级课时练习）定义：有一个角是其对角一半的圆的内接四边形叫做圆美四边形，其中这个角叫做美角．已知四边形ABCD是圆美四边形．

（1）求美角∠A的度数；
（2）如图1，若⊙O的半径为5，求BD的长；
（3）如图2，若CA平分∠BCD，求证：BC+CD=AC．
培优训练
一、解答题
1．（2022·辽宁葫芦岛·一模）射线AB与直线CD交于点E，∠AED＝60°，点F在直线CD上运动，连接AF，线段AF绕点A顺时针旋转60°得到AG，连接FG，EG，过点G作GH⊥AB于点H．
(1)如图1，点F和点G都在射线AB的同侧时，EG与GH的数量关系是______；
(2)如图2，点F和点G在射线AB的两侧时，线段EF，AE，GH之间有怎么样的数量关系？并证明你的结论；
(3)若点F和点G都在射线AB的同侧，AE=1，EF=2，请直接写出HG的长．
2．（2022·上海宝山·九年级期末）如图，已知正方形ABCD，将AD绕点A逆时针方向旋转n°(0(1)求证：CE=EF；
(2)联结CF，如果DPCF=13，求∠ABP的正切值；
(3)联结AF，如果AF=22AB，求n的值．
3．（2022·重庆市育才中学九年级期末）在等边△ABC中，D是边AC上一动点，连接BD，将BD绕点D顺时针旋转120°，得到DE，连接CE．
（1）如图1，当B、A、E三点共线时，连接AE，若AB=2，求CE的长；
（2）如图2，取CE的中点F，连接DF，猜想AD与DF存在的数量关系，并证明你的猜想；
（3）如图3，在（2）的条件下，连接BE、AF交于G点．若GF=DF，请直接写出CD+ABBE的值．
4．（2022·黑龙江·哈尔滨工业大学附属中学校九年级期末）在平面直角坐标系中，抛物线y＝3ax2﹣10ax＋c分别交x轴于点A、B（A左B右）、交y轴于点C，且OB＝OC＝6．
（1）如图1，求抛物线的解析式；
（2）如图2，点P在第一象限对称轴右侧抛物线上，其横坐标为t，连接BC，过点P作BC的垂线交x轴于点D，连接CD，设△BCD的面积为S，求S与t的函数关系式（不要求写出t的取值范围）；
（3）如图3，在（2）的条件下，线段CD的垂直平分线交第二象限抛物线于点E，连接EO、EC、ED，且∠EOC＝45°，点N在第一象限内，连接DN，DN∥EC，点G在DE上，连接NG，点M在DN上，NM＝EG，在NG上截取NH＝NM，连接MH并延长交CD于点F，过点H作HK⊥FM交ED于点K，连接FK，若∠FKG＝∠HKD，GK＝2MN，求点G的坐标．

5．（2021·广东·珠海市紫荆中学九年级期中）如图，△ABC中，∠BAC＝90°，AB＝AC＝4，直角△ADE的边AE在线段AC上，AE＝AD＝2，将△ADE绕直角顶点A按顺时针旋转一定角度α，连接CD、BE，直线CD，BE交于点F，连接AF，过BC中点G作GM⊥CD，GN⊥AF．
（1）求证：BE＝CD；
（2）求证：旋转过程中总有∠BFA＝∠MGN；（仅对0°＜α＜90°时加以证明）
（3）在AB上取一点Q，使得AQ＝1，求FQ的最小值．
6．（2021·湖北·武汉外国语学校（武汉实验外国语学校）九年级阶段练习）【问题背景】如图1，P是等边△ABC内一点，∠APB＝150°，则PA2+PB2＝PC2．小刚为了证明这个结论，将△PAB绕点A逆时针旋转60°，请帮助小刚完成辅助线的作图；
【迁移应用】如图2，D是等边△ABC外一点，E为CD上一点，AD∥BE，∠BEC＝120°，求证：△DBE是等边三角形；
【拓展创新】如图3，EF＝6，点C为EF的中点，边长为3的等边△ABC绕着点C在平面内旋转一周，直线AE、BF交于点P，M为PG的中点，EF⊥FG于F，FG＝43，请直接写出MC的最小值．
7．（2022·全国·九年级课时练习）如图1，在正方形ABCD中，点F在边BC上，过点F作EF⊥BC，且FE=FC(CE（1）用等式表示线段BF与FG的数量关系：______；
（2）将图1中的△CEF绕点C按逆时针旋转，使△CEF的顶点F恰好在正方形ABCD的对角线AC上，点G仍是AE的中点，连接FG、DF．
①在图2中，依据题意补全图形；
②用等式表示线段DF与FG的数量关系并证明．
8．（2021·四川·成都实外九年级阶段练习）“数学建模”是中学数学的核心素养，平时学习过程中能归纳一些几何模型，解决几何问题就能起到事半功倍的作用．
（1）如图1，正方形ABCD中，∠EAF=45°，且DE=BF，求证：EG=AG；
（2）如图2，正方形ABCD中，∠EAF=45°，延长EF交AB的延长线于点G，（1）中的结论还成立吗？请说明理由；
（3）如图3在（2）的条件下，作GQ⊥AE，垂足为点Q，交AF于点N，连结DN，求证：∠NDC=45°．
9．（2021·上海徐汇·九年级期中）如图，已知Rt△ABC和Rt△CDE，∠ACB=∠CDE=90°，∠CAB=∠CED，AC=8，BC=6，点D在边AB上，射线CE交射线BA于点F．
（1）如图，当点F在边AB上时，联结AE．
①求证：AE∥BC；
②若EF=12CF，求BD的长；
（2）设直线AE与直线CD交于点P，若△PCE为等腰三角形，求BF的长．
10．（2022·全国·九年级专题练习）定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．
（1）如图1，∠E是△ABC中∠A的遥望角．
①若∠A＝40°，直接写出∠E的度数是 ；
②求∠E与∠A的数量关系，并说明理由．
（2）如图2，四边形ABCD中，∠ABC＝∠ADC＝90°，点E在BD的延长线上，连CE，若∠BEC是△ABC中∠BAC的遥望角，求证：DA＝DE．
11．（2022·全国·九年级课时练习）在正方形ABCD中，M是BC边上一点，点P在射线AM上，将线段AP绕点A顺时针旋转90°得到线段AQ，连接BP，DQ．
（1）如图1，求证：BP=DQ；
（2）如图2，若点P，B，D三点共线，求证：A，Q，P，D四点共圆；
（3）若点P，Q，C三点共线，且AD=3，求BP的长．
12．（2021·江苏·泗阳县实验初级中学九年级阶段练习）如图1，在正方形ABCD中，点E、F分别是BC、CD上的两个动点，且BE=CF，AE和BF相交于点P．
（1）探究AE、BF的关系，并说明理由；
（2）求证：A、D、F、P在同一个圆上；
（3）如图2，若正方形ABCD的边AB在y轴上，点A、B的坐标分别为(0,−1+a)、(0,−1−a)，点E、F分别是BC、CD上的两个点，且BE=CF，AE和BF相交于点P，点M的坐标为(4,−4)，当点P落在以M为圆心1为半径的圆上．求a的取值范围．
13．（2021·重庆一中九年级阶段练习）如图，在等腰Rt△ABC中，∠BAC=90°，AD⊥BC，垂足为D，点E为AC边上一点，连接ED并延长至F，使ED=FD，以EF为底边作等腰Rt△EGF．
（1）如图1，若∠ADE=30°，AE=4，求CE的长；
（2）如图2，连接BF，DG，点M为BF的中点，连接DM，过D作DH⊥AC，垂足为H，连接AG交DH于点N，求证：DM=NG；
（3）如图3，点K为平面内不与点D重合的任意一点，连接KD，将KD绕点D顺时针旋转90°得到K′D，连接K′A，KB，直线K′A与直线KB交于点P，D′为直线BC上一动点，连接AD′并在AD′的右侧作C′D′⊥AD′且C′D′=AD′，连接AC′，Q为BC边上一点，CD=3CQ，AB=122，当QC′+C′P取到最小值时，直线C′P与直线BC交于点S，请直接写出△BPS的面积．
14．（2021·福建省福州外国语学校三模）在Rt△ABC中，∠ACB=90°，AC=3，BC=4．将Rt△ABC绕点B顺时针旋转α(0°<α<60°)得到Rt△DEB，直线DE，AC交于点P．
（1）如图1，当BD⊥BC时，连接BP．
①求△BDP的面积；
②求tan∠CBP的值；
（2）如图2，连接AD，若F为AD中点，求证；C，E，F三点共线．
15．（2021·黑龙江·哈尔滨市虹桥初级中学校模拟预测）直线y=kx+k与x轴交于A，与y轴交于C点，直线BC的解析式为y=−1kx+k，与x轴交于B．
（1）如图1，求点A的横坐标；
（2）如图2，D为BC延长线上一点，过D作x轴垂线于点E，连接CE，若CD=CA，设△ACE的面积为S，求S与k的函数关系式；
（3）如图3，在（2）的条件下，连接OD交AC于点F，将△CDF沿CF翻折得到△FCG，直线FG交CE于点K，若3∠ACE−∠CDO=45°，求点K的坐标．
16．（2021·全国·九年级课时练习）在平行四边形ABCD中，已知∠A＝45°，AD⊥BD，点E为线段BC上的一点，连接DE，以线段DE为直角边构造等腰Rt△DEF，EF交线段AB于点G，连接AF、DG．
（1）如图1，若AB＝122，BE＝5，则DE的长为多少？
（2）如图2，若点H，K分别为线段BG，DE的中点，连接HK，求证：AG＝2HK；
（3）如图3，在（2）的条件下，若BE＝2，BG＝22，以点G为圆心，AG为半径作⊙G，点M为⊙G上一点，连接MK，取MK的中点P，连接AP，请直接写出线段AP的取值范围．
17．（2021·江苏苏州·二模）如图（1），已知矩形ABCD中，AB=6cm，BC=23cm，点E为对角线AC上的动点．连接BE，过E作EB的垂线交CD于点F．
（1）探索BE与EF的数量关系，并说明理由．
（2）如图（2），过F作AC垂线交AC于点G，交EB于点H，连接CH．若点E从A出发沿AC方向以23cm/s的速度向终点C运动，设E的运动时间为ts．
①是否存在t，使得H与B重合？若存在，求出t的值；若不存在，说明理由；
②t为何值时，△CFH是等腰三角形；
③当CG=GH时，求△CGH的面积．
18．（2022·江苏扬州·模拟预测）如图，将一副斜边相等的直角三角板按斜边重合摆放在同一平面内，其中∠DAB＝45°，∠CAB＝30°，点O为斜边AB的中点，连接CD交AB于点E．设AB＝1．
（1）求证：A、B、C、D四个点在以点O为圆心的同一个圆上；
（2）分别求△ABC和△ABD的面积；
（3）过点D作DF∥BC交AB于点F，求OE︰OF的比值．
19．（2021·江苏南京·二模）如图①，A是⊙O外一点，AB与⊙O相切于点B，AO的延长线交⊙O于点C，过点B作BD//AC，交⊙O于点D，连接DO，并延长DO交⊙O于点E，连接AE．已知BD=2，⊙O的半径为3．
（1）求证：AE是⊙O的切线；
（2）求AE的长；
（3）如图②，若点M是⊙O上一点，且BM=3，过A作AN//BM，交弧ME于点N，连接ME，交AN于点G，连接OG，则OG的长度是______．
20．（2020·浙江温州·九年级期中）如图，在▱ABCD中，AB=5,tanA=43，过点B作BE⊥AD于点E，过B，D，E三点的圆分别交边AB，BC，CD于点F，M，N，连结BE，CE，连结BN交CE于点P．
（1）求证：EF=MN．
（2）当△BPE是等腰三角形时，求AD的长．
（3）连结BD，MN，当BD平分∠ADC时，求△BMN与△CDE面积的比值．
21．（2020·湖南·郴州市第九中学九年级阶段练习）如图，边长为32的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°得到BQ，连接QP，QP与BC交于点E，其延长线与AD（或AD延长线）交于点F．

（1）连接CQ，证明：CQ=AP；
（2）设AP=x，CE=y，试写出y关于x的函数关系式，并写出自变量x的取值范围；
（3）试问当P点运动到何处时，PB+PE的值最小，并求出此时CE的长．（画出图形，直接写出答案即可）
22．（2021·全国·九年级课时练习）如图，四边形ABCD内接于⊙O，对角线AC⊥BD，垂足为E，CF⊥AB于点F，直线CF与直线BD于点G．
（1）若点G在⊙O内，如图1，求证：G和D关于直线AC对称；
（2）连接AG，若AG=BC，且AG与⊙O相切，如图2，求∠ABC的度数．
23．（2020·北京市三帆中学九年级期中）已知：过⊙O上一点A作两条弦AB、AC，且∠A=45°，（AB、AC都不经过O）过A作AC的垂线AF，交⊙O于D，直线BD，AC交于点E，直线BC，AD交于点F.
（1）请在图1中，按要求补全图形；
（2）在图2中探索线段BE和BF的数量关系，并证明你的结论；
（3）探索线段AB、AE、AF的数量关系，并直接写出你的结论________.
24．（2020·湖北·武汉二中广雅中学二模）如图，等腰Rt△ABC中，∠ACB＝90°，D为BC边上一点，连接AD．
（1）如图1，作BE⊥AD延长线于E，连接CE，求证：∠AEC＝45°；
（2）如图2，P为AD上一点，且∠BPD＝45°，连接CP．
①若AP＝2，求△APC的面积；
②若AP＝2BP，直接写出sin∠ACP的值为______．