最新中考数学压轴大题之经典模型 专题17 角平分线的四大模型-【压轴必刷】

这是一份最新中考数学压轴大题之经典模型 专题17 角平分线的四大模型-【压轴必刷】，文件包含专题17角平分线的四大模型-压轴必刷2023年中考数学压轴大题之经典模型培优案原卷版docx、专题17角平分线的四大模型-压轴必刷2023年中考数学压轴大题之经典模型培优案解析版docx等2份试卷配套教学资源，其中试卷共69页， 欢迎下载使用。

今天整理了初三中考总复习阶段在教学过程中收集的经典题目，一共有31讲，包括原卷版和解析版，供大家学习复习参考。
经典题目1：这是一道非常经典的最值问题，最值模型将军饮马和一箭穿心。
经典题目2：上面三道题是费马点经典问题，旋转转化是费马点问题的关键。
经典题目3：阿氏圆经典题目，这道题目实际包括了隐圆模型，一箭穿心模型等常见几何模型。
经典题目4：这是中考出现频率比较高的胡不归问题，也是经典最值问题。
【压轴必刷】2023年中考数学压轴大题之经典模型培优案
专题17角平分线的四大模型
解题策略
经典例题
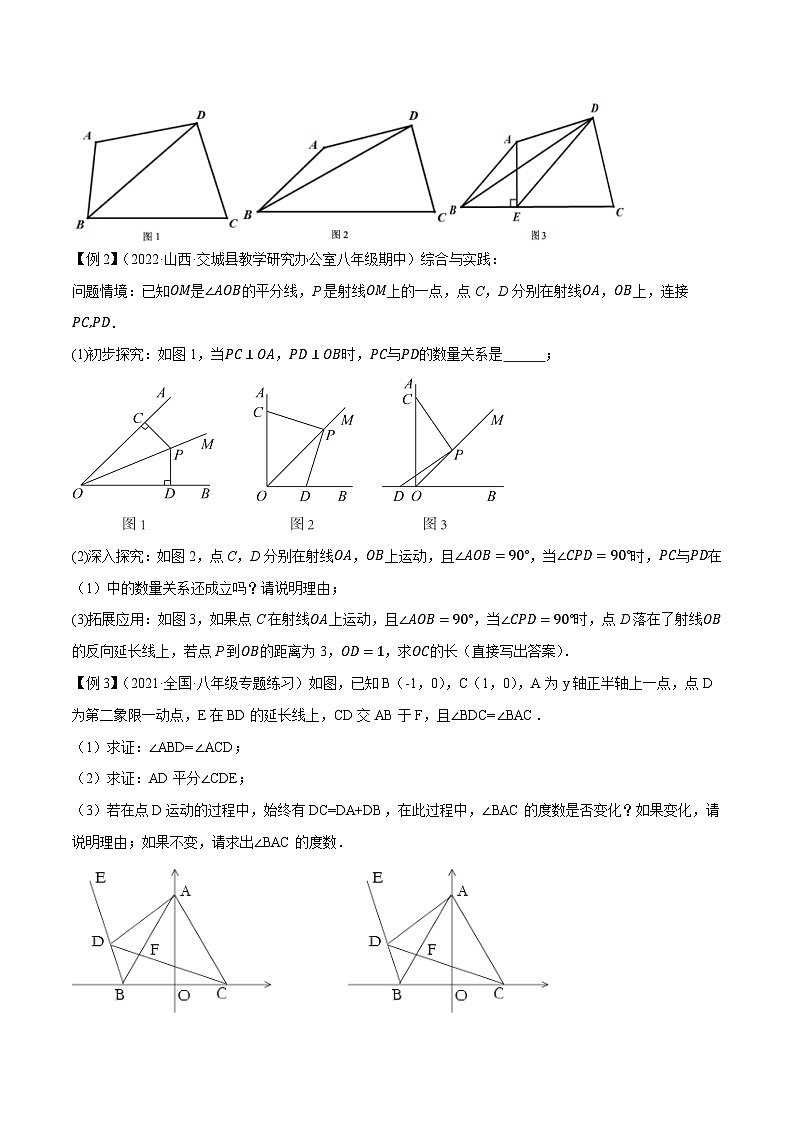
【例1】（2022·黑龙江·哈尔滨市第六十九中学校八年级阶段练习）四边形ABCD中，DA=DC，连接BD．
（1）如图1，若BD平分∠ABC，求证：∠A+∠C=180°．
（2）如图2，若BD=BC，∠BAD=150°，求证：∠DBC=2∠ABD．
（3）如图3，在（2）的条件下，作AE⊥BC于点E，连接DE，若DA⊥DC，BC=2，求DE的长度．
【例2】（2022·山西·交城县教学研究办公室八年级期中）综合与实践：
问题情境：已知OM是∠AOB的平分线，P是射线OM上的一点，点C，D分别在射线OA，OB上，连接PC,PD．
(1)初步探究：如图1，当PC⊥OA，PD⊥OB时，PC与PD的数量关系是 ；
(2)深入探究：如图2，点C，D分别在射线OA，OB上运动，且∠AOB=90°，当∠CPD=90°时，PC与PD在（1）中的数量关系还成立吗？请说明理由；
(3)拓展应用：如图3，如果点C在射线OA上运动，且∠AOB=90°，当∠CPD=90°时，点D落在了射线OB的反向延长线上，若点P到OB的距离为3，OD=1，求OC的长（直接写出答案）．
【例3】（2021·全国·八年级专题练习）如图，已知B（-1，0），C（1，0），A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC=∠BAC．
（1）求证：∠ABD=∠ACD；
（2）求证：AD平分∠CDE；
（3）若在点D运动的过程中，始终有DC=DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数．
【例4】（2021·贵州·九年级专题练习）【特例感知】
（1）如图（1），∠ABC是⊙O的圆周角，BC为直径，BD平分∠ABC交⊙O于点D，CD=3，BD=4，求点D到直线AB的距离．
【类比迁移】（2）如图（2），∠ABC是⊙O的圆周角，BC为⊙O的弦，BD平分∠ABC交⊙O于点D，过点D作DE⊥BC，垂足为点E，探索线段AB，BE，BC之间的数量关系，并说明理由．
【问题解决】（3）如图（3），四边形ABCD为⊙O的内接四边形，∠ABC=90°，BD平分∠ABC，BD=72，AB=6，求△ABC的内心与外心之间的距离．
培优训练
一、解答题
1．（2022·全国·八年级课时练习）已知：如图，在四边形ABCD中，BD平分∠ABC，∠A+∠C＝180°，BC＞BA．求证：点D在线段AC的垂直平分线上．
2．（2022·全国·八年级课时练习）如图，△ABC中，AC＝BC，∠ACB＝90°，AD平分∠BAC交BC于点D，过点B作BE⊥AD，交AD延长线于点E，F为AB的中点，连接CF，交AD于点G，连接BG．
（1）线段BE与线段AD有何数量关系？并说明理由；
（2）判断△BEG的形状，并说明理由．
3．（2022·江苏·八年级专题练习）在△ABC中，AD为△ABC的角平分线，点E是直线BC上的动点．
（1）如图1，当点E在CB的延长线上时，连接AE，若∠E＝48°，AE＝AD＝DC，则∠ABC的度数为 ．
（2）如图2，AC＞AB，点P在线段AD延长线上，比较AC+BP与AB+CP之间的大小关系，并证明．
（3）连接AE，若∠DAE＝90°，∠BAC＝24°，且满足AB+AC＝EC，请求出∠ACB的度数（要求：画图，写思路，求出度数）．
4．（2022·全国·八年级课时练习）如图，在△ABC中，∠C＝90°，AD是∠BAC的角平分线，交BC于点D，过D作DE⊥BA于点E，点F在AC上，且BD＝DF．
（1）求证：AC＝AE；
（2）若AB＝7.4，AF＝1.4，求线段BE的长．
5．（2022·江苏·八年级专题练习）如图1，在△ABC中，CM是AB边的中线，∠BCN=∠BCM交AB延长线于点N，2CM=CN．

（1）求证AC=BN；
（2）如图2，NP平分∠ANC交CM于点P，交BC于点O，若∠AMC=120°，CP=kAC，求CPCM的值．
6．（2022·全国·八年级课时练习）（1）如图1，射线OP平分∠MON，在射线OM，ON上分别截取线段OA，OB，使OA＝OB，在射线OP上任取一点D，连接AD，BD．求证：AD＝BD．
（2）如图2，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB，求证：BC＝AC+AD．
（3）如图3，在四边形ABDE中，AB＝9，DE＝1，BD＝6，C为BD边中点，若AC平分∠BAE，EC平分∠AED，∠ACE＝120°，求AE的值．
7．（2022·全国·八年级课时练习）已知：AD是△ABC的角平分线，且AD⊥BC．
（1）如图1，求证：AB=AC；
（2）如图2，∠ABC=30°，点E在AD上，连接CE并延长交AB于点F，BG交CA的延长线于点G，且∠ABG=∠ACF，连接FG．
①求证：∠AFG=∠AFC；
②若S△ABG:S△ACF=2:3，且AG=2，求AC的长．
8．（2022·全国·八年级）如图1，在△ABC中，AF，BE分别是∠BAC和∠ABC的角平分线，AF和BE相交于D点．
（1）求证：CD平分∠ACB；
（2）如图2，过F作FP⊥AC于点P，连接PD，若∠ACB=45°，∠PDF=67.5°，求证：PD=CP；
（3）如图3，若2∠BAF+3∠ABE=180°，求证：BE−BF=AB−AE．
9．（2022·湖南·宁远县至善学校八年级阶段练习）在平面直角坐标系中，点A的坐标是(0,a)，点B的坐标(b,0)且a，b满足a2−12a+36+a−b=0．
（1）求A、B两点的坐标；
（2）如图（1），点C为x轴负半轴一动点，OC（3）如图（2），点F为AB的中点，点G为x正半轴点B右侧的一动点，过点F作FG的垂线FH，交y轴的负半轴于点H，那么当点G的位置不断变化时，S△AFH−S△FBG的值是否发生变化?若变化，请说明理由；若不变化，请求出相应结果．
10．（2022·全国·八年级课时练习）已知：如图，AC∥BD，AE、BE分别平分∠CAB和∠ABD，点E在CD上．用等式表示线段AB、AC、BD三者之间的数量关系，并证明．
11．（2022·全国·八年级课时练习）已知点C是∠MAN平分线上一点，∠BCD的两边CB、CD分别与射线AM、AN相交于B，D两点，且∠ABC+∠ADC＝180°．过点C作CE⊥AB，垂足为E．
（1）如图1，当点E在线段AB上时，求证：BC＝DC；
（2）如图2，当点E在线段AB的延长线上时，探究线段AB、AD与BE之间的等量关系；
（3）如图3，在（2）的条件下，若∠MAN＝60°，连接BD，作∠ABD的平分线BF交AD于点F，交AC于点O，连接DO并延长交AB于点G．若BG＝1，DF＝2，求线段DB的长．
12．（2022·全国·八年级）在平面直角坐标系中，点A−5,0，B0,5，点C为x轴正半轴上一动点，过点A作AD⊥BC交y轴于点E．
（1）如图①，若点C的坐标为（3，0），试求点E的坐标；
（2）如图②，若点C在x轴正半轴上运动，且OC<5，其它条件不变，连接DO，求证：OD平分∠ADC
（3）若点C在x轴正半轴上运动，当∠OCB=2∠DAO时，试探索线段AD、OC、DC的数量关系，并证明．
13．（2022·全国·八年级）如图1，点A是直线MN上一点，点B是直线PQ上一点，且MN//PQ．∠NAB和∠ABQ的平分线交于点C．
（1）求证：BC⊥AC；
（2）过点C作直线交MN于点D（不与点A重合），交PQ于点E,
①若点D在点A的右侧，如图2，求证：AD+BE=AB；
②若点D在点A的左侧，则线段AD、BE、AB有何数量关系？直接写出结论，不说理由．
14．（2018·湖北武汉·八年级期中）在平面直角坐标中，等腰Rt△ABC中，AB=AC，∠CAB=90°，A（0，a），B（b，0）．
（1）如图1，若2a−b+（a-2）2=0，求△ABO的面积；
（2）如图2，AC与x轴交于D点，BC与y轴交于E点，连接DE，AD=CD，求证：∠ADB=∠CDE；
（3）如图3，在（1）的条件下，若以P（0，-6）为直角顶点，PC为腰作等腰Rt△PQC，连接BQ，求证：AP∥BQ．
15．（2018·辽宁·沈阳市第一四三中学八年级期末）阅读下面材料：小明遇到这样一个问题:
如图一，△ABC中，∠A=90°，AB=AC，BD平分∠ABC，猜想线段AD与DC数量关系.小明发现可以用下面方法解决问题:作DE⊥BC交BC于点E：
(1)根据阅读材料可得AD与DC的数量关系为__________.
(2)如图二，△ABC中，∠A=120°，AB=AC，BD平分∠ABC，猜想线段AD与DC的数量关系，并证明你的猜想.
(3)如图三，△ABC中，∠A=100°，AB=AC，BD平分∠ABC，猜想线段AD与BD、BC的数量关系，并证明你的猜想.

16．（2019·全国·九年级专题练习）已知：ΔABC中，D为BC的中点，AG平分∠BAC,CG⊥AG于G，连结DG，若AB=6,AC=4，求DG的长．
17．（2022·全国·八年级课时练习）在△ABC中，BE，CD为△ABC的角平分线，BE，CD交于点F．
（1）求证：∠BFC=90°+12∠A；
（2）已知∠A=60°．
①如图1，若BD=4，BC=6.5，求CE的长；
②如图2，若BF=AC，求∠AEB的大小．
18．（2022·广东·金辉学校九年级阶段练习）已知：如图，在Rt△ABC中，∠C=90∘，AC=1，BC=3，动点O从点C出发，沿着C→B→A→C的方向运动一周，以O为圆心，r为半径作圆．
(1)若⊙O分别与AB，BC相切．
①利用直尺和圆规作⊙O（不写作法，保留作图痕迹）；
②求出此r时的值；
(2)当r=1时，设⊙O在运动的过程中与△ABC三条边的公共点个数为m，那么m的最小值是___________，最大值是___________．
19．（2022·四川·石室中学八年级期中）如图，在△ABC中，已知AD是BC边上的高，过点B作BE⊥AC于点E，交AD于点F，且AD=65，BD=25，CD=35．
(1)求BEAB的值；
(2)求证：AF=BC；
(3)如图2，在（2）的条件下，在ED的延长线上取一点G，使BG=BE，请猜想DG与DE的数量关系，并说明理由．
20．（2022·江苏徐州·八年级期中）如图，在Rt△ABC中，∠ACB=90°，AB=10cm，AC=6cm，动点P从点B出发沿射线BC以1cm/s的速度运动，设运动时间为ts．
(1)直接写出BC=______cm；
(2)当AP平分∠BAC时，求t的值；
(3)当△ABP为等腰三角形时，求t的值．