中考数学复习指导：在变中寻找不变求解几何问题

这是一份中考数学复习指导：在变中寻找不变求解几何问题，共4页。试卷主要包含了原题，变式等内容，欢迎下载使用。
一、原题
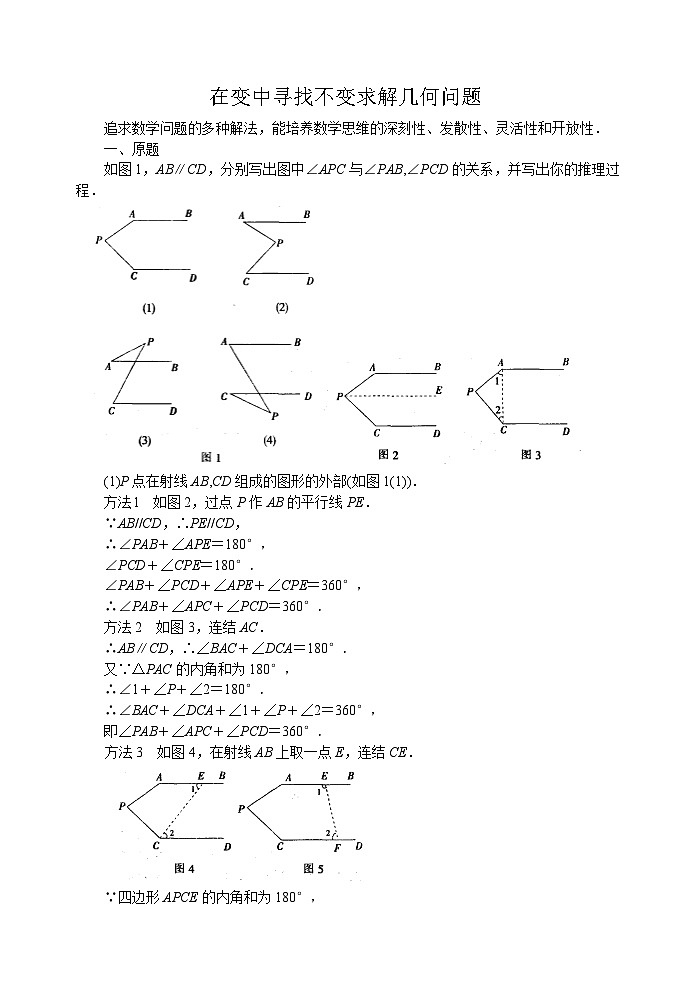
如图1，AB∥CD，分别写出图中∠APC与∠PAB,∠PCD的关系，并写出你的推理过程．
(1)P点在射线AB,CD组成的图形的外部(如图1(1))．
方法l 如图2，过点P作AB的平行线PE．
∵AB//CD，∴PE//CD，
∴∠PAB＋∠APE＝180°，
∠PCD＋∠CPE＝180°．
∠PAB＋∠PCD＋∠APE＋∠CPE＝360°，
∴∠PAB＋∠APC＋∠PCD＝360°．
方法2 如图3，连结AC．
∴AB∥CD，∴∠BAC＋∠DCA＝180°．
又∵△PAC的内角和为180°，
∴∠1＋∠P＋∠2＝180°．
∴∠BAC＋∠DCA＋∠1＋∠P＋∠2＝360°，
即∠PAB＋∠APC＋∠PCD＝360°．
方法3 如图4，在射线AB上取一点E，连结CE．
∵四边形APCE的内角和为180°，
∴∠1＋∠A＋∠P＋∠PCE＝360°．
又∵AB∥CD，∴∠1＝∠2，
∴∠2＋∠A＋∠P＋∠PCE＝360°，
即∠PAB＋∠APC＋∠PCD＝360°．
方法4 如图5，分别在射线AB.CD上任取一点E,F，连结EF．
∵五边形APCE的内角和为540°，
∴∠1＋∠A＋∠P＋∠C＋∠2＝540°．
又∵AB∥CD，∴∠1＋∠2＝180°，
∴∠A＋∠P＋∠C＝360°，
即∠PAB＋∠APC＋∠PCD＝360°．
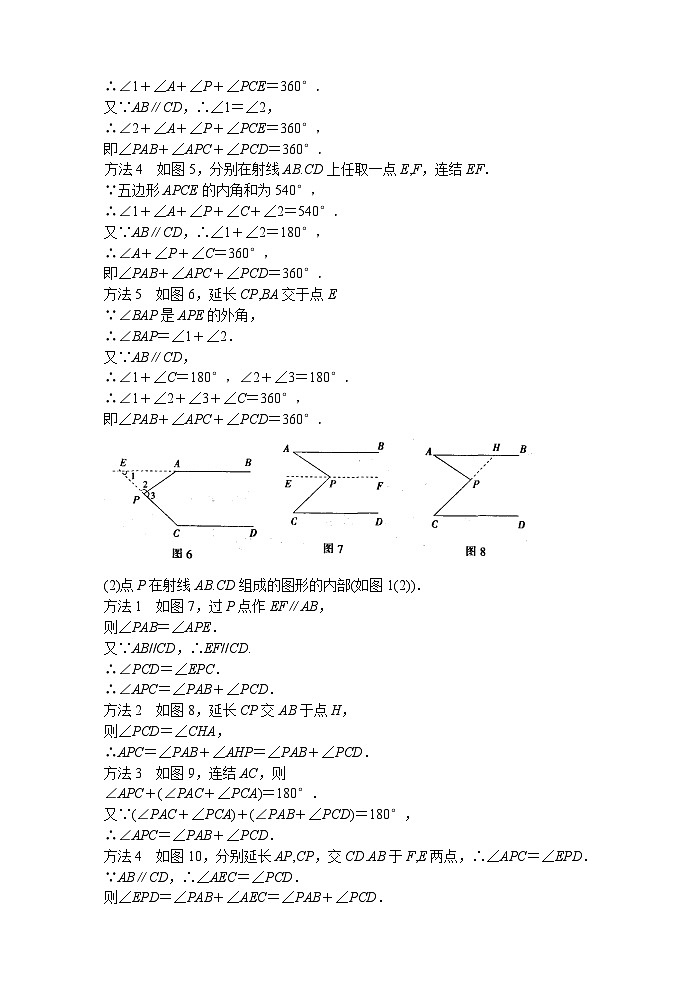
方法5 如图6，延长CP,BA交于点E
∵∠BAP是APE的外角，
∴∠BAP＝∠1＋∠2．
又∵AB∥CD，
∴∠1＋∠C＝180°，∠2＋∠3＝180°．
∴∠1＋∠2＋∠3＋∠C＝360°，
即∠PAB＋∠APC＋∠PCD＝360°．
(2)点P在射线AB.CD组成的图形的内部(如图1(2))．
方法1 如图7，过P点作EF∥AB，
则∠PAB＝∠APE．
又∵AB//CD，∴EF//CD.
∴∠PCD＝∠EPC．
∴∠APC＝∠PAB＋∠PCD．
方法2 如图8，延长CP交AB于点H，
则∠PCD＝∠CHA，
∴APC＝∠PAB＋∠AHP＝∠PAB＋∠PCD．
方法3 如图9，连结AC，则
∠APC＋(∠PAC＋∠PCA)＝180°．
又∵(∠PAC＋∠PCA)＋(∠PAB＋∠PCD)＝180°，
∴∠APC＝∠PAB＋∠PCD．
方法4 如图10，分别延长AP,CP，交CD.AB于F,E两点，∴∠APC＝∠EPD．
∵AB∥CD，∴∠AEC＝∠PCD．
则∠EPD＝∠PAB＋∠AEC＝∠PAB＋∠PCD．
∴∠APC＝∠PAB＋∠PCD．
方法5 如图11，过点P作PE⊥AB，延长EP交CD于点F，则EF⊥CD．
∠APE＋∠PAB＋∠AEP＝180°，
∠CPF＋∠PCD＋∠PFC＝180°．
∵∠AEP＝90°，∠PFC＝90°，
∴(∠APE＋∠CPF)＋(∠PAB＋∠PCD)＝180°．
又∵(∠APE＋∠CPF)＋∠APC＝180°，
∴∠APC＝∠PAB＋∠PCD．
当然，本题的解法还有很多，聪明的你能否再找出几种呢？
仿照思路可以解决图1 (3)和图1(4)．
点评 无论点P的位置如何发生改变，都可以运用平行线的性质或内角和、外角的性质来找出各个角之间的关系，只要用心发现、探索，必然会发现其中的规律．
二、变式
变式l 将直线AB绕点B逆时针方向旋转一定角度，交直线CD于点Q，如图12，则∠BPD,∠B,∠D,∠BQD之间有何数量关系？
解 连结QP并延长至F．
∵∠BPF是△PBQ的外角，
∴∠BPF＝∠B＋∠BQP，
同理可得∠DPF＝∠D＋∠DQP．
∴∠BPF＋∠DPF＝∠B＋∠BQP＋∠D＋∠DQP，
即∠BPD＝∠B＋∠D＋∠BQD．
变式2 求图13中∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．
解由图12的结论，得
∠AGB＝∠A＋∠B＋∠E．
又∵ ∠AGB＝∠CGF，
∠CGF＋∠C＋∠D＋LF＝360°，
∴ ∠A＋∠B＋∠C＋∠D∠E＋∠F＝360°．