




辽宁省沈阳市康平县2023-2024学年九年级下学期随堂练习(月考)数学试题(原卷版+解析版)
展开一、选择题(下列各题的备选答案中,只有一个是正确的,每小题3分,计30分)
1. 北京时间2月25日晚,2024年世界乒乓球团体锦标赛在韩国釜山落下帷幕.中国男、女队双双登顶,分别夺取11连冠和6连冠.图①是乒乓球男团颁奖现场,图②是领奖台的示意图,则此领奖台主视图是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查主视图.主视图是从几何体正面观察到的视图.
【详解】解:领奖台从正面看,是由三个长方形组成的.三个长方形,右边最低,中间最高,
故选:B.
2. 在四边形中,,添加下列条件不能推得四边形为菱形的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据菱形定义及其判定、矩形的判定对各选项逐一判断即可得.
【详解】A选项:若AB=CD,∵AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
B选项:当AD∥BC时,又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
C选项:当BC=CD时,△ABD≌△BCD(SSS),
∴∠A=∠C,
∵AB∥CD,
∴∠C+∠ABC=180°,
∴∠A+∠ABC=180°,
∴AD∥BC,
又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
D选项只能说明四边形的三条边相等,所以不能判定是菱形.
故选D.
【点睛】本题主要考查菱形的判定,解题的关键是掌握菱形的定义.
3. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )
A. B. C. D.
【答案】D
【解析】
【分析】利用矩形的性质证明△AOB是等边三角形,即可求得AB的长.
【详解】解:∵∠AOD=120°,
∴∠AOB=60°,
∵四边形ABCD是矩形,
∴OA=OC=AC=OB=OD=BD=4(cm),
∴△AOB是等边三角形,
∴AB=OA=4(cm),
故选:D.
【点睛】本题考查了矩形的性质,等边三角形的判定和性质,熟记矩形和等边三角形的性质并准确识图是解题的关键.
4. 科技承载梦想,创新始于少年,某校科技社团的学生制作了一艘轮船模型,实验过程中他们发现在某段航行过程中轮船模型的牵引力是其速度的反比例函数,其图象如图所示,下列说法不正确的是( )
A. 该段航行过程中,随的增大而减小B. 时,
C. 该段航行过程中,函数表达式为D. 时,
【答案】B
【解析】
【分析】本题考查了反比例函数的应用,熟练掌握反比例函数性质是解答本题的关键.根据图象和反比例函数的性质,逐项判断各项的正误即可.
【详解】解:A、根据图象可知,是定值,F随v的增大而减小,选项正确,不符合题意;
B、根据图象可知,当时,,选项错误,符合题意;
C、根据图象可知,函数表达式为,选项正确,不符合题意;
D、由,当1时,,选项正确,不符合题意.
故选:B.
5. 下列说法中,正确的是( )
A. 等弦所对的弧相等B. 等弧所对的弦相等
C. 圆心角相等,所对的弦相等D. 弦相等所对的圆心角相等
【答案】B
【解析】
【分析】根据圆心角,弦,弧之间的关系判断,注意条件.
【详解】A中,等弦所对应的弧可以相等也可以互补构成新圆;
B中,等弧所对应的弦相等,故选B
C中,圆心角相等所对应的弦可能互补;
D中,弦相等,圆心角可能互补;
故选B
【点睛】本题考查了圆心角,弧,弦之间的观,此类试题属于难度较大的试题,其中,弦和圆心角等一些基本知识容易混淆,从而很难把握.
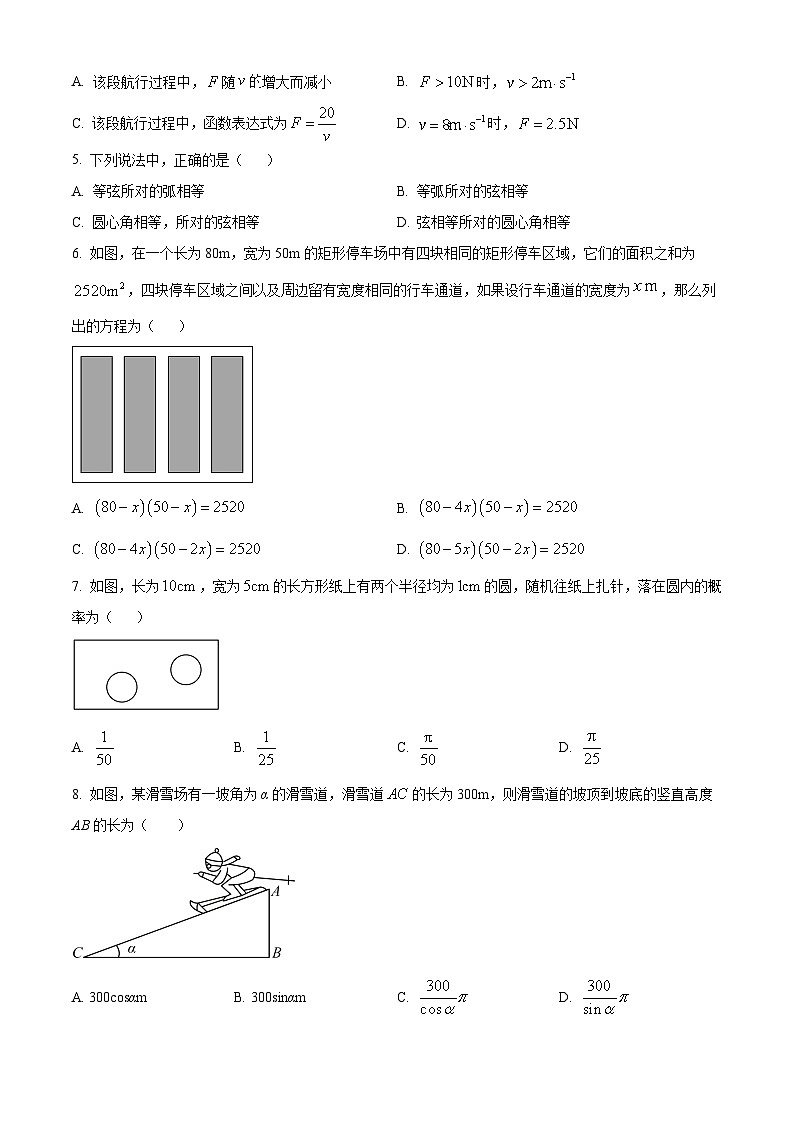
6. 如图,在一个长为80m,宽为50m的矩形停车场中有四块相同的矩形停车区域,它们的面积之和为,四块停车区域之间以及周边留有宽度相同的行车通道,如果设行车通道的宽度为,那么列出的方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查一元二次方程解决实际问题.设行车通道的宽度为,则停车区域的长总和为,宽总和为,根据“它们的面积之和为”即可列出方程.
【详解】设行车通道的宽度为.根据题意,得
.
故选:D.
7. 如图,长为,宽为的长方形纸上有两个半径均为的圆,随机往纸上扎针,落在圆内的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】本题考查几何概率的求法:注意圆、长方形的面积计算.用到的知识点为:概率=相应的面积与总面积之比.分别求出圆和长方形的面积,它们的面积比即为针落在阴影部分的概率.
【详解】解:长方形的面积,
两个圆的总面积是:,
则针落在阴影部分的概率是;
故选D.
8. 如图,某滑雪场有一坡角为α的滑雪道,滑雪道的长为300m,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A. 300csαmB. 300sinαmC. D.
【答案】B
【解析】
【分析】本题考查了解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念,熟记锐角三角函数的定义是解题的关键.
根据正弦的定义进行解答即可.
【详解】解:在中,,,,
∵,
∴,
故选:B.
9. 如图,已知两个直角三角形关于原点位似,且点与点是对应顶点,则的值为( )
A. 2B. C. 18D.
【答案】A
【解析】
【分析】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或-.利用关于以原点为位似中心的对应点的坐标变换规律,横坐标的比等于纵坐标的比.
【详解】解:∵两三角形关于原点位似,且一对对应点的坐标分别为,,
∴,
∴.
故选:A.
10. 如图,抛物线与x轴交于点A,B两点,与y轴负半轴交于点C,其顶点为M,点D,E分别是的中点,若与的面积比为9∶10,则c的值为( )
A. B. C. D.
【答案】C
【解析】
【分析】由题意可得,,由点D是的中点,与的面积比为9∶10,得到,由中点坐标公式得,,,M为顶点,求得点M的横坐标,代入解析式,由纵坐标相等得到关于c的方程,解之即可得到答案.
【详解】解:由题意可得,,,
∵点D是的中点,
∴,
∵与的面积比为9∶10,
∴,
∴,
∵E是的中点,
∴由中点坐标公式得,,
当时,,
∴,
∴,
∵,,
∴,
∵M为顶点,
∴,
将代入得,
,
解得 ,
故选:C
【点睛】此题考查了二次函数的面积综合题,求得是解题的关键.
二、填空题(每小题3分,计15分)
11. 读一读下面的诗词:大江东去浪淘尽,千古风流数人物;而立之年督东吴,早逝英年两位数;十位恰小个位三,个位平方与寿同.诗词大意是周瑜三十岁当上了东吴都督,去世时年龄是两位数,十位数比个位数小3,个位数的平方等于他去世时的年龄,若设他去世时年龄的个位数为x,则根据题意可列出方程______.
【答案】
【解析】
【分析】设他去世时年龄的个位数为x,则设他去世时年龄的十位数为,然后根据个位数的平方等于他去世时的年龄列出方程即可.
【详解】解:设他去世时年龄的个位数为x,则设他去世时年龄的十位数为,
由题意得,,
故答案为:.
【点睛】本题主要考查了从实际问题中抽象出一元二次方程,正确理解题意找到等量关系是解题的关键.
12. 在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是____________.
【答案】6
【详解】如图,连接AC,∵ 在矩形ABCD中,AB=8,AD=6,∠ABC=90°,
∴AC====10,
∴AD
∴点D一定在⊙A内,点C一定在⊙A外,
∴⊙A半径r取值范围应大于AD的长,小于对角线AC的长,即6
【答案】26
【解析】
【分析】由OA=22知道抛物线经过点A(22,0),进而求出k的值,最高点与其在水中倒影之间的距离即为2k.
【详解】解:由题意知OA=22,抛物线经过点A(22,0),代入解析式中:
得到:,求得,
∴抛物线顶点坐标为(11,13),
∴主桥拱最高点与其在水中倒影之间的距离为2×13=26,
故答案为:26米.
【点睛】本题考查了二次函数的图形和性质,点在函数图像上,将点的坐标代入,等号两边相等即可求出某些参数的值.
14. 如图,菱形的边在x轴上,点,,若反比例函数的图象经过点C,则k的值为______.
【答案】12
【解析】
【分析】本题考查菱形的性质,锐角三角函数的定义以及求反比例函数的解析式.根据菱形的性质和锐角三角函数求出点的坐标是解题的关键.
根据菱形的性质和点的坐标可求出,再由锐角三角函数可求出,进而确定点的坐标,再将点的坐标代入函数关系式即可求解.
【详解】解:过点作的垂线交于,如图:
四边形是菱形,,
,
又,
,
点,
点在反比例函数的图象上,
,
故答案为:12.
15. 如图,AB是⊙O的直径,AB=10,BC、CD、DA是⊙O的弦,且BC=CD=DA,若点P是直径AB上的一动点,则PD+PC的最小值为_____.
【答案】10
【解析】
【分析】作出点C关于AB的对称点C′,连接C′D,根据轴对称确定最短路线问题,C′D与AB的交点即为所求的点P,连接CP,根据同弧所对的圆周角等于圆心角的一半求出∠B=60°,然后求出AB∥CD,再求出∠BCD=120°,再求出∠BCC′=30°,然后求出∠C′CD=90°,从而判断出C′D为圆的直径.
【详解】如图,作出点C关于AB的对称点C′,连接C′D,
则C′D与AB的交点即为所求的点P,连接CP,C′D=PC+PD,
∵AB是⊙O的直径,BC=CD=DA,
∴∠B=××180°=60°,
∵AD=BC,
∴AB∥CD,
∴∠BCD=120°,
∴∠BCC′=×60°=30°,
∴∠C′CD=120°-30°=90°,
∴C′D为圆的直径,
∵AB是⊙O的直径,AB=10,
∴PD+PC的最小值为10,
故答案为10.
【点睛】本题考查了轴对称确定最短路线问题,圆周角定理,垂径定理,以及弧、圆心角、弦之间的关系,熟记各性质并求出C′D是圆的直径是解题的关键.
三、解答题(本题共8小题,共75分,解答应写出文字说明、演算步骤或推理过程)
16. 计算:.
【答案】.
【解析】
【分析】本题考查了特殊角的三角函数值.代入特殊角的三角函数值,利用实数的运算法则计算即可求解.
【详解】解:
.
17. 李白是唐朝伟大的浪漫主义诗人,被后人誉为“诗仙”.《行路难·其一》是李白不受重用,求仕无望后满怀愤慨所作的名篇.王铭和李虹将这首诗中的四句分别写在编号为A,B,C,D的4张卡片上,如图所示,卡片除编号和内容外,其余完全相同,将这4张卡片背面朝上,洗匀放好,玩抽诗句的游戏.
(1)王铭从中抽取一张卡片,恰好抽到“长风破浪会有时”的概率为________;
(2)李虹先抽一张卡片,接着王铭从剩下的卡片中抽一张,用画树状图或列表的方法求两人所抽卡片上的诗句恰好成联(注:A与B为一联,C与D为一联)的概率.
【答案】(1)
(2).
【解析】
【分析】本题考查列表法与树状图法、概率公式.
(1)直接利用概率公式可得答案.
(2)列表可得出所有等可能的结果数以及两人所抽卡片上的诗句恰好成联的结果数,再利用概率公式可得出答案.
【小问1详解】
解:由题意得,王铭从中抽取一张卡片,恰好抽到“长风破浪会有时”的概率为.
故答案为:;
【小问2详解】
解:列表如下:
共有12种等可能的结果,其中两人所抽卡片上的诗句恰好成联的结果有:,,,,共4种,
∴两人所抽卡片上的诗句恰好成联的概率为.
18. 如图所示,以的顶点A为圆心,AB的长为半径作圆,与分别交于点E,F,延长交于点G.求证:.
【答案】见解析
【解析】
【分析】本题考查圆的有关知识“在同圆或等圆中相等的圆心角所对的弧相等”;利用平行四边形的性质证得,,再通过等腰三角形的性质得到,从而证得,据此即可证明.
【详解】证明:连接,
∵四边形是平行四边形,
∴,
∴,,
∵,
∴,
∴,
∴.
19. 如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF,求证:四边形AECF是菱形.
【答案】见解析
【解析】
【分析】根据对角线互相垂直的平行四边形是菱形即可证明
【详解】证明:四边形是平行四边形,
,,
,
,,
四边形是平行四边形,
,
四边形是菱形.
【点睛】本题考查平行四边形的性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
20. 如图①是位于青岛的山东省内最大的海景摩天轮“琴岛之眼”,游客可以在碧海蓝天之间领略大青岛的磅礴气势.图②是它的简化示意图,点O是摩天轮的圆心,是摩天轮垂直地面的直径,小红在E处测得摩天轮顶端A的仰角为,她沿水平方向向左行走到达点D,再沿着坡度的斜坡走了20米到达点C,然后再沿水平方向向左行走到达摩天轮最低点B处(A,B,C,D,E均在同一平面内),求摩天轮的高度.(结果保留整数)(参考数据:)
【答案】摩天轮的高度约68米
【解析】
【分析】本题考查了解直角三角形的应用——仰角俯角问题,通过作辅助线,构造直角三角形是解题关键.延长交的延长线于点M,过点C作于点N,在中,求得,在中,利用三角函数解出即可求出结论.
【详解】解:延长交的延长线于点M,过点C作于点N,
由题意得,,
∴四边形是矩形,
,
在中,设,
由勾股定理得,
,
,
,
在中,,
,
,
,
,
答:摩天轮的高度约68米.
21. 如图,在△ABC中,AB=AC=10,BC=12,点D,E分别在边BC,AC上(点D不与端点B,C重合),并且满足∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)设BD=x,CE=y,请求出当x取何值时,y取最大值?y的最大值是多少?
(3)当△ADE是等腰三角形时,求BD的长.
【答案】(1)见解析 (2)当时,有最大值,最大值为;
(3)当x=2或时,△ADE是等腰三角形,
【解析】
分析】(1)先判断出∠ADB=∠DEC,即可得出结论;
(2)借助(1)的相似三角形得出比例式即可得出函数关系式,由0<x<16,即可得出y的范围;
(3)根据等腰三角形的判定与性质,可得∠ADC与∠DAC的关系,根据三角形的外角的性质,可得∠AED的大小,根据等腰三角形的判定,可得答案;
【小问1详解】
解:∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠ADB=180°-∠ADE-∠CDE,∠DEC=180°-∠C-∠CDE,
∴∠ADB=∠DEC,
∵∠B=∠C,
∴△ABD∽△DCE;
【小问2详解】
∵BD=x,CE=y,
∴DC=BC-BD=12-x,
由(1)知,△ABD∽△DCE,
∴,
∴,
∴
∵,且
∴当时,有最大值,最大值为;
【小问3详解】
①当DA=DE时,
∴∠DAE=∠AED,
∵AB=AC=10,
∴∠B=∠C=∠ADE.
∵∠AED=∠EDC+∠C=∠EDC+∠ADE,
∴∠DAE=∠EDC+∠ADE,
∴∠EAD=∠ADC,
∴CD=AC=10,
∴x=BD=BC-CD=12-10=2,
所以,当x的长为2时,△ADE是等腰三角形,
②当AE=DE时,△ADE是等腰三角形,即∠DAE=∠ADE=∠B
又∠ACD=∠BCA,
∴△ADC∽△BAC,
∴,
∴DC•BC=AC2,
∴DC=,
∴x=BD=12-DC=12-;
综上所述:当x=2或时,△ADE是等腰三角形,
【点睛】本题主要考查了等腰三角形、相似三角形的性质和判定,明确等边对等角和等角对等边,相似三角形常用的判定是:两角对应相等的两个三角形相似,在几何证明中常利用相似得比例式求边的长度;同时又运用了同角的余角求角相等;本题还运用了分类讨论的思想,尤其动点形成的三角形是直角三角形或等腰三角形时,要根据具体问题分情况进行讨论.
22. 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点分别在正方形的边上,,连接,则,试说明理由.
(1)思路梳理
∵,∴把绕点逆时针旋转至,可使与重合.
∵,∴,点共线,
证明得.
请按此思路说明原题中的成立的理由.
(2)类比引申
如图2,四边形中,,点分别在边上,.若都不是直角,则当与满足怎样的关系时,仍有;请说明理由.
(3)联想拓展
如图3,在中,,点均在边上,且.猜想应满足的等量关系,并写出推理过程.
【答案】(1)见解析 (2)时,;理由见解析
(3)猜想:,理由见解析
【解析】
【分析】()把绕点逆时针旋转至,使与重合,证明,根据全等三角形性质得出,即可得出答案;
()把绕点逆时针旋转至,使与重合,证明,根据全等三角形的性质得出,即可得出答案;
()把绕点逆时针旋转到的位置,连接,证明,则,,是直角三角形,
根据勾股定理即可作出判断.
【小问1详解】
证明:如图中,
∵,
∴把绕点逆时针旋转至, 与重合,
∵,
∴ ,点、、 共线,
则,,,
即,
在和中,
,
∴,
∴;
【小问2详解】
解:时,;理由如下:
∵,
把绕点逆时针旋转至,可使与重合,如图所示:
∴,,
∵,,
∴,
∴,
∵,
∴,点、、共线,
在和中,
,
∴,
∴,
∵,
∴;
【小问3详解】
解:猜想:,理由如下:
把绕点逆时针旋转到的位置,连接,如图所示,
则,,
∴,,,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴ ,
∵,,
∴,
∴ ,
∴,
∴是直角三角形,
∴,
∴.
【点睛】此题考查了全等三角形的性质和判定,正方形的性质,等腰直角三角形的性质、勾股定理等知识,能正确作出辅助线得出全等三角形是解题的关键.
23. 定义:对于抛物线(、、是常数,),若,则称该抛物线是黄金抛物线,已知平面直角坐标系,抛物线是黄金抛物线,与轴交于点,顶点为.
(1)求此黄金抛物线的表达式及点坐标;
(2)点在这个黄金抛物线上.
①点在这个黄金抛物线的对称轴上,求的正弦值.
②在射线上是否存在点,使以点、、所组成的三角形与相似,且相似比不为1.若存在,请求出点的坐标;若不存在,请说明理由.
【答案】(1),
(2)①,②存在,
【解析】
【分析】本题考查二次函数的综合应用,相似三角形的判定和性质.利用数形结合,分类讨论的思想进行求解.
(1)根据黄金抛物线的定义,列出方程求出值,进而求出顶点的坐标即可;
(2)①将点代入解析式,求出的值,求出对称轴,得到的值,进而求出的长,勾股定理逆定理,得到,利用正弦的定义,求解即可;
②分和,两种情况进行讨论求解即可.
【小问1详解】
解:抛物线是黄金抛物线,
,
所求抛物线的表达式为,
配方得:,
点的坐标为;
【小问2详解】
解:①由(1)得:抛物线的对称轴是直线,
点的坐标为,
点在这个黄金抛物线上,
,
,
点的坐标为,
,
,
,
,
,
;
②存在,
过点作,垂足为,
抛物线与轴交于点,
点的坐标为,
点的坐标为,
,
,
点的坐标为,
,
,
,
,
要使以点、、所组成的三角形与相似,有两种情况
①,
又,,
∴与全等,相似比为1,不合题意,舍去;
②,
∵,
,
,
,
,,
,
点在射线上,
点的坐标为.A
欲渡黄河冰塞川
B
将登太行雪满山
C
长风破浪会有时
D
直挂云帆济沧海
辽宁省沈阳市皇姑区2022-2023学年七年级下学期期末数学试题(解析版+原卷版): 这是一份辽宁省沈阳市皇姑区2022-2023学年七年级下学期期末数学试题(解析版+原卷版),文件包含精品解析辽宁省沈阳市皇姑区2022-2023学年七年级下学期期末数学试题原卷版docx、精品解析辽宁省沈阳市皇姑区2022-2023学年七年级下学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
辽宁省沈阳市铁西区2022-2023学年七年级下学期期末数学试题(原卷版+解析版): 这是一份辽宁省沈阳市铁西区2022-2023学年七年级下学期期末数学试题(原卷版+解析版),文件包含精品解析辽宁省沈阳市铁西区2022-2023学年七年级下学期期末数学试题原卷版docx、精品解析辽宁省沈阳市铁西区2022-2023学年七年级下学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
辽宁省沈阳市沈河区2022-2023学年七年级下学期期末数学试题(原卷版+解析版): 这是一份辽宁省沈阳市沈河区2022-2023学年七年级下学期期末数学试题(原卷版+解析版),文件包含精品解析辽宁省沈阳市沈河区2022-2023学年七年级下学期期末数学试题原卷版docx、精品解析辽宁省沈阳市沈河区2022-2023学年七年级下学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。












