第19讲 全等三角形课件---2024年中考数学一轮复习

这是一份第19讲 全等三角形课件---2024年中考数学一轮复习，共29页。PPT课件主要包含了综合模拟练，基础全练，答案不唯一，挑战高分，中考创新练等内容，欢迎下载使用。
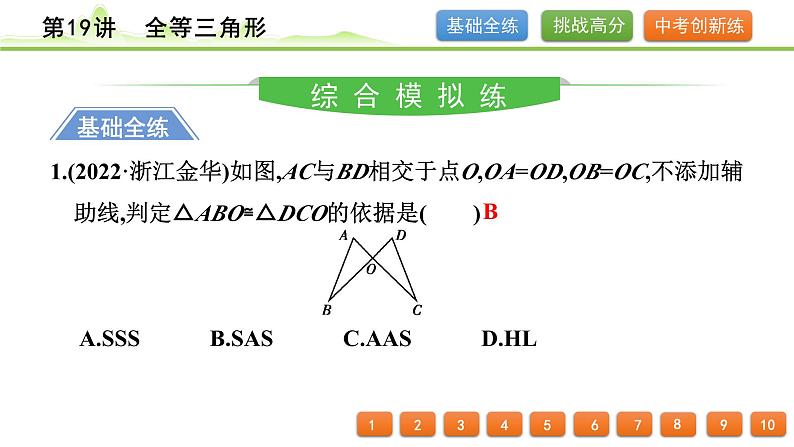
1.(2022·浙江金华)如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是(　　) A.SSS　　　B.SAS　　　C.AAS　　　D.HL
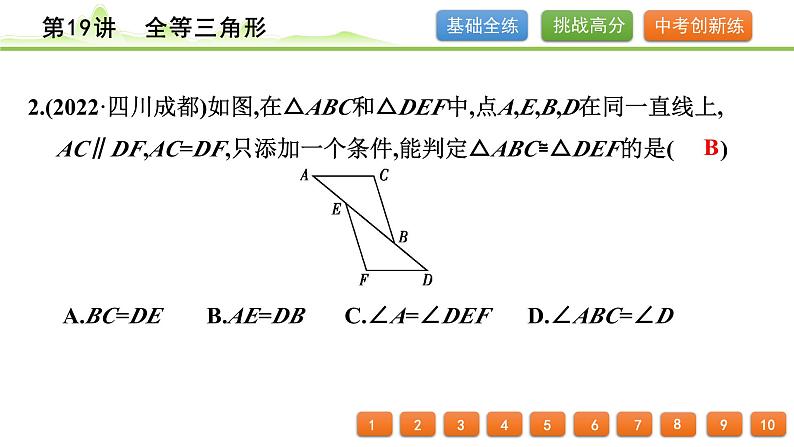
2.(2022·四川成都)如图,在△ABC和△DEF中,点A,E,B,D在同一直线上, AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF的是(　　) A.BC=DEB.AE=DB C.∠A=∠DEF D.∠ABC=∠D
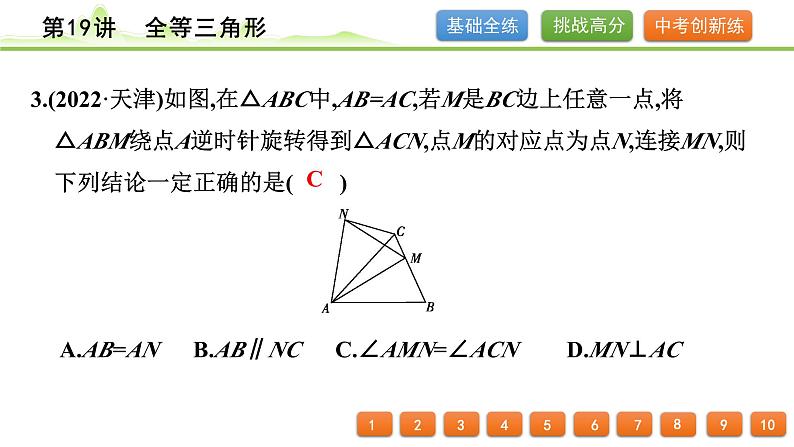
3.(2022·天津)如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是(　　) A.AB=AN B.AB∥NC C.∠AMN=∠ACND.MN⊥AC
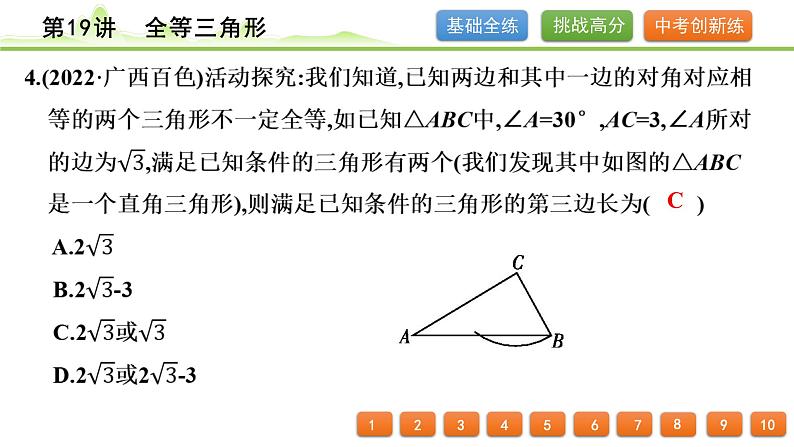
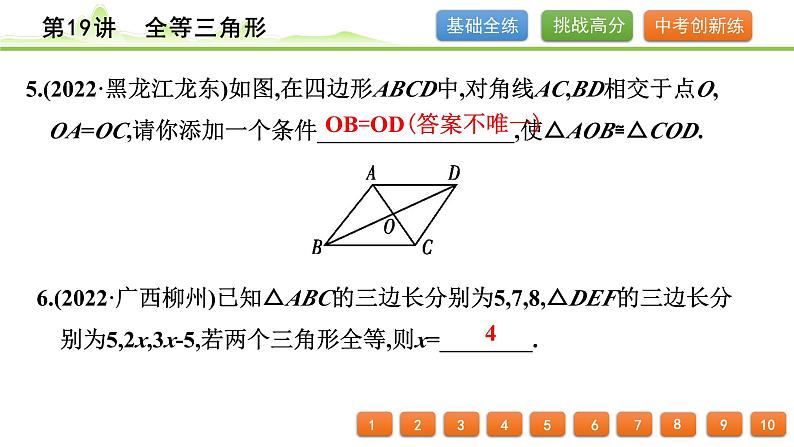
5.(2022·黑龙江龙东)如图,在四边形ABCD中,对角线AC,BD相交于点O, OA=OC,请你添加一个条件_________________,使△AOB≌△COD. 
OB=OD(答案不唯一)
6.(2022·广西柳州)已知△ABC的三边长分别为5,7,8,△DEF的三边长分别为5,2x,3x-5,若两个三角形全等,则x=________. 
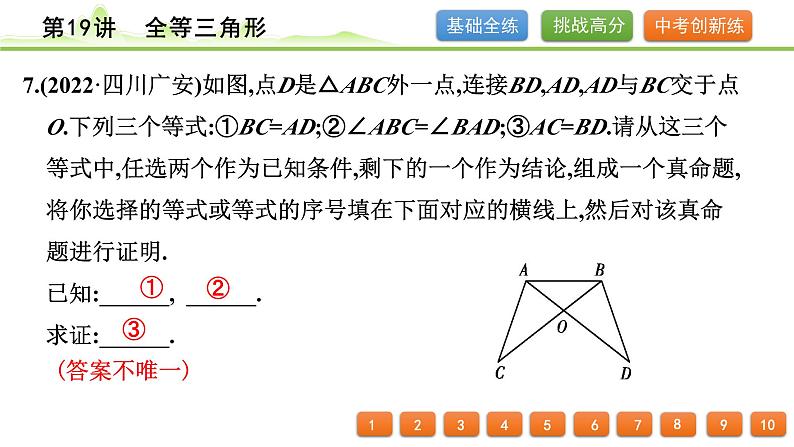
7.(2022·四川广安)如图,点D是△ABC外一点,连接BD,AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC=BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明. 已知:______, ______.  求证:______. 
8.(2022·湖南长沙)如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为B,D. (1)求证:△ABC≌△ADC; (2)若AB=4,CD=3,求四边形ABCD的面积.
9.(2022·陕西)如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE= ∠A.求证:DE=BC.
证明:∵DE∥AB,∴∠EDC=∠B.又∵CD=AB,∠DCE=∠A,∴△CDE≌△ABC(ASA).∴DE=BC.
10.(2022·浙江宁波)如图,△ACB和△ECD都是等腰直角三角形,∠ACB= ∠ECD=90°.A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F. (1)求证:△ACE≌△BCD; (2)直线AE与BD互相垂直吗?请证明你的结论.
(1)证明:∵△ACB和△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACE=∠BCD=90°,∴△ACE≌△BCD;
(2)解:直线AE与BD互相垂直,证明:∵△ACE≌△BCD,∴∠EAC=∠DBC,又∵∠DBC+∠CDB=90°,∴∠EAC+∠CDB=90°,∴∠AFD=90°,∴AF⊥BD,即直线AE与BD互相垂直.
11.(2022·广西玉林)问题情境: 在数学探究活动中,老师给出了如图的图形及下面三个等式: ①AB=AC;②DB=DC;③∠BAD=∠CAD.若以其中两个等式作为已知条件,能否得到余下一个等式成立? 解决方案:探究△ABD与△ACD全等.
问题解决:(1)当选择①②作为已知条件时,△ABD与△ACD全等吗?_______(填“全等”或“不全等”),理由是_____________________; (2)当任意选择两个等式作为已知条件时,请用画树状图法或列表法求△ABD≌△ACD的概率.
(1)全等,理由:三边对应相等的两个三角形全等;
12.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E. (1)当∠BDA=115°时,∠EDC=______,∠DEC=_______;  (2)当DC等于多少时,△ABD≌△DCE,请说明理由; (3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
解:(1)当∠BDA=115°时,∠EDC=180°-115°-40°=25°,在△DEC中,∠DEC=180°-∠EDC-∠C=115°,故答案为:25°,115°;(2)当DC=2时,△ABD≌△DCE,理由如下:∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,　∠B=∠ADE=40°,∴∠BAD=∠EDC,∵∠B=∠C=40°,△ABD≌△DCE,∴AB=DC=2;
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,理由如下:∵∠B=∠C=40°,∠B+∠C+∠BAC=180°,∴∠BAC=180°-∠B-∠C=180°-40°-40°=100°.分三种情况讨论:①当DA=DE时,∠DAE=∠DEA,∵∠ADE=40°,∠ADE+∠DAE+∠DEA=180°,∴∠DAE=(180°-40°)÷2=70°,∴∠BAD=∠BAC-∠DAE=100°-70°=30°,∵∠B+∠BAD+∠BDA=180°,∴∠BDA=180°-∠B-∠BAD=180°-40°-30°=110°;
②当AD=AE时,∠AED=∠ADE=40°,∵∠ADE+∠AED+∠DAE=180°,∴∠DAE=180°-∠AED-∠ADE=180°-40°-40°=100°,又∵∠BAC=100°,∴∠DAE=∠BAE,∴点D与点B重合,不合题意;
③当EA=ED时,∠DAE=∠ADE=40°,　∴∠BAD=∠BAC-∠DAE=100°-40°=60°,　∵∠B+∠BAD+∠BDA=180°,∴∠BDA=180°-∠B-∠BAD=180°-40°-60°=80°.综上所述,当∠BDA的度数为110°或80°时,△ADE是等腰三角形.
13.如图,OB平分∠AOC,D,E,F分别是射线OA,射线OB,射线OC上的点,D,E,F与O点都不重合,连接ED,EF.若添加下列条件中的某一个,就能使△DOE≌△FOE.你认为要添加的那个条件是(　　) A.OD=OE B.OE=OF C.∠ODE=∠OED D.∠ODE=∠OFE
14.如图,正方形格点图中,点A,B,C,D,E,F均在格点上,若以D,E,F为顶点的三角形与△ABC全等,请写出一个满足条件的F点坐标________. 
(4,-2)(答案不唯一)
15.已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°. (1)如图1,连接AM,BN,求证:△AOM和△BON全等; (2)如图2,将△MON绕点O顺时针旋转,当点N恰好在AB边上时,求证:BN²+AN²=2ON².
证明:(1)∵∠AOB=∠MON=90°,∴∠AOB+∠AON=∠MON+∠AON,即∠AOM=∠BON,　∵△AOB和△MON都是等腰直角三角形,∴OA=OB,OM=ON,∴△AOM≌△BON(SAS);
(2)连接AM,如图.∵∠AOB=∠MON=90°,∴∠AOB-∠AON=∠MON-∠AON,即∠AOM=∠BON,∵△AOB和△MON都是等腰直角三角形,∴OA=OB,OM=ON,∴△AOM≌△BON(SAS),∴∠MAO=∠NBO=45°,AM=BN,∴∠MAN=90°,∴AM²+AN²=MN²,∵△MON是等腰直角三角形,∴MN²=2ON²,∴BN²+AN²=2ON².
(2)证明:如图1,连接EF,由(1)得∠DAF=∠DBE=45°,AD=BD,∵BE=AF,∴△DAF≌△DBE(SAS),∴DF=DE,∠ADF=∠BDE,∴AD⊥BC,∴∠ADB=90°,即∠BDE+∠ADE=90°,　∴∠ADF+∠ADE=90°,即∠EDF=90°,　∵DF=DE,∴△DEF是等腰直角三角形;