第25讲 点与圆、直线与圆的位置关系课件---2024年中考数学一轮复习

这是一份第25讲 点与圆、直线与圆的位置关系课件---2024年中考数学一轮复习，共35页。PPT课件主要包含了综合模拟练，基础全练，挑战高分，中考创新练等内容，欢迎下载使用。

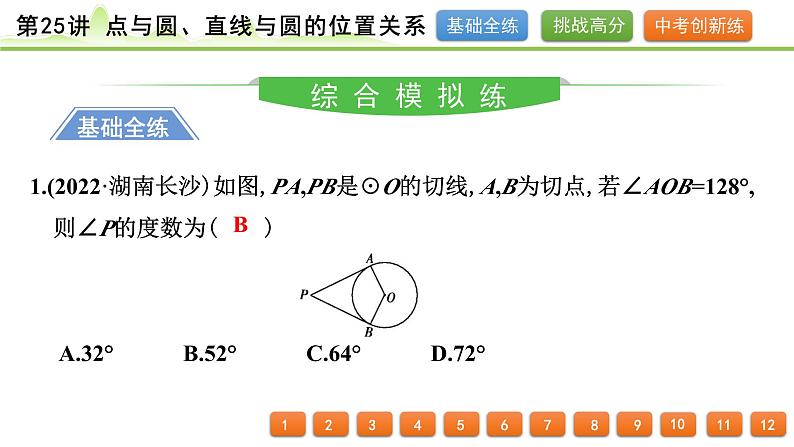
1.(2022·湖南长沙)如图,PA,PB是☉O的切线,A,B为切点,若∠AOB=128°,则∠P的度数为(　　) A.32°　　　B.52°　　　C.64°　　　D.72°
2.(2022·江苏无锡)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是(　　) A.AE⊥DE B.AE∥OD C.DE=OD D.∠BOD=50°
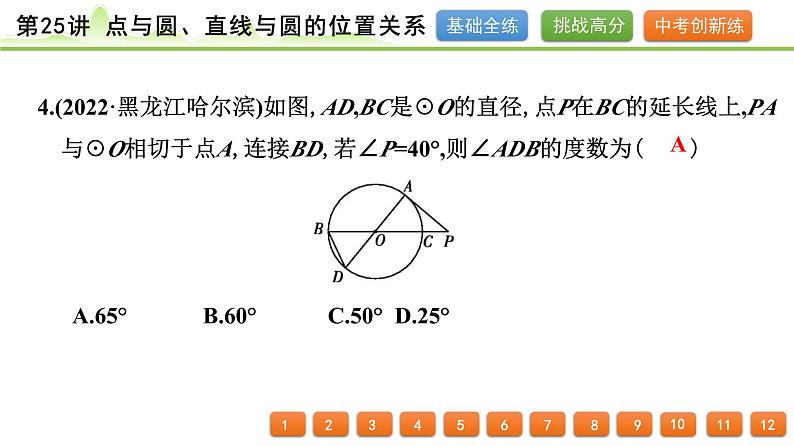
4.(2022·黑龙江哈尔滨)如图,AD,BC是☉O的直径,点P在BC的延长线上,PA与☉O相切于点A,连接BD,若∠P=40°,则∠ADB的度数为(　　) A.65° B.60° C.50°D.25°
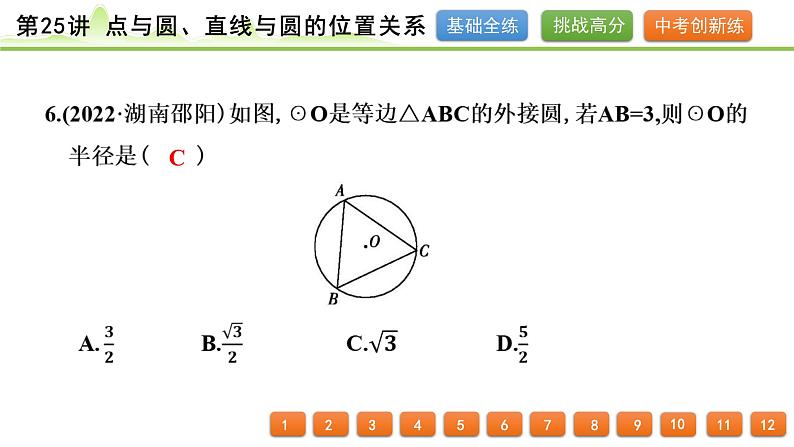
5.(2022·湖北十堰)如图,☉O是等边△ABC的外接圆,点D是弧AC上一动点(不与A,C重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有(　　) A.1个 B.2个 C.3个 D.4个
8.(2022·海南)如图,射线AB与☉O相切于点B,经过圆心O的射线AC与☉O相交于点D,C,连接BC,若∠A=40°,则∠ACB=_______°. 
9.(2022·贵州黔东南)如图,在△ABC中,∠A=80°,半径为3 cm的☉O是 △ABC的内切圆,连接OB,OC,则图中阴影部分的面积是______cm².(结果用含π的式子表示) 
10.(2022·湖南邵阳)如图,已知DC是☉O的直径,点B为CD延长线上一点,AB是☉O的切线,点A为切点,且AB=AC. (1)求∠ACB的度数; (2)若☉O的半径为3,求圆弧AC的长.
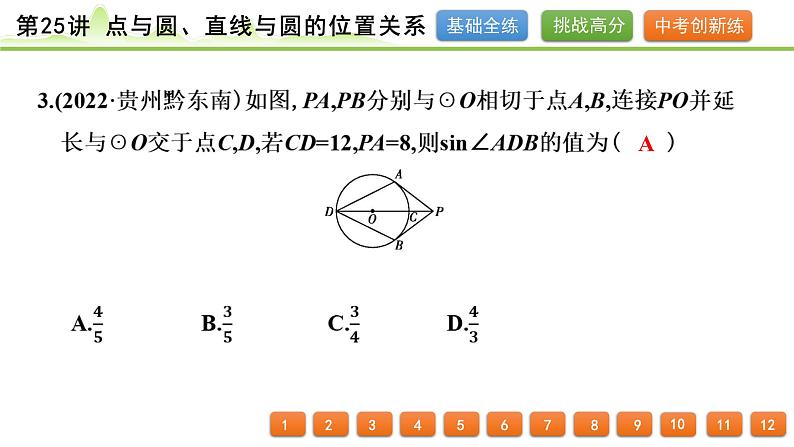
解:(1)PC与☉O相切,理由如下:∵AB是圆O的直径,∴∠ACB=90°,∴∠OCB+∠OCA=90°,∵OA=OC,∴∠OCA=∠OAC,∵∠PCB=∠OAC,∴∠PCB=∠OCA,∴∠PCB+∠OCB=∠OCA+∠OCB=90°,即∠PCO=90°,∴PC与☉O相切;
12.(2022·河南)为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环☉O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环☉O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.
(1)证明:∵☉O与水平地面相切于点C,∴OC⊥CD,∵AD⊥CD,∴AD∥OC,∵AB与☉O相切于点B,∴AB⊥OB,∴∠OBA=90°,过点B作BE∥AD,如图1,∴∠BAD=∠EBA,∴BE∥OC,∴∠COB=∠OBE,∴∠COB+∠BAD=∠OBE+∠ABE=∠OBA=90°,即∠BOC+∠BAD=90°;
14.(2022·湖北恩施州)如图,P为☉O外一点,PA,PB为☉O的切线,切点分别为A,B,直线PO交☉O于点D,E,交AB于点C. (1)求证:∠ADE=∠PAE; (2)若∠ADE=30°,求证:AE=PE; (3)若PE=4,CD=6,求CE的长.
(1)证明:如图,连接OA,∵PA为☉O的切线,∴OA⊥PA,即∠OAP=90°,∴∠OAE+∠PAE=90°,∵DE为☉O的直径,∴∠DAE=90°,即∠OAE+∠DAO=90°,　∴∠DAO=∠PAE,∵OA=OD,∴∠DAO=∠ADE,∴∠ADE=∠PAE;(2)证明:∵∠ADE=30°,∴∠ADE=∠PAE=30°,∠AED=90°-∠ADE=60°,∴∠APE=∠AED-∠PAE=30°,∴∠APE=∠PAE=30°,∴AE=PE;
15.(2022·贵州贵阳)如图,AB为☉O的直径,CD是☉O的切线,C为切点,连接BC.ED垂直平分OB,垂足为E,且交BC于点F,交BC于点P,连接BF,CF. (1)求证:∠DCP=∠DPC; (2)当BC平分∠ABF时,求证:CF∥AB; (3)在(2)的条件下,OB=2,求阴影部分的面积.
(1)证明:如图1,连接CO,∵DC为☉O的切线,∴∠OCD=∠OCB+∠DCP=90°.∵DE⊥AB,∴∠BPE+∠PBE=90°.∵OC=OB,∴∠OCB=∠OBC,∵∠DPC=∠BPE,∴∠DCP=∠DPC;
17.(2022·江苏泰州)如图,△ABC中,∠C=90°,AC=8,BC=6,O为内心,过点O的直线分别与AC,AB相交于D,E,若DE=CD+BE,则线段CD的长 为_______. 
解:(1)相切,理由如下:连接OD,如图1所示.∵BD为∠ABC的平分线,∴∠ABD=∠CBD.又∵☉O过点B,D,设☉O半径为r,∴OB=OD=r,∴∠ODB=∠OBD=∠CBD.∴OD∥BC(内错角相等,两直线平行).∵OD⊥AC,∴AC与☉O的位置关系为相切;