初中数学21.1 一元二次方程精品巩固练习

这是一份初中数学21.1 一元二次方程精品巩固练习，文件包含第05讲一元二次方程的实际应用原卷版docx、第05讲一元二次方程的实际应用解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

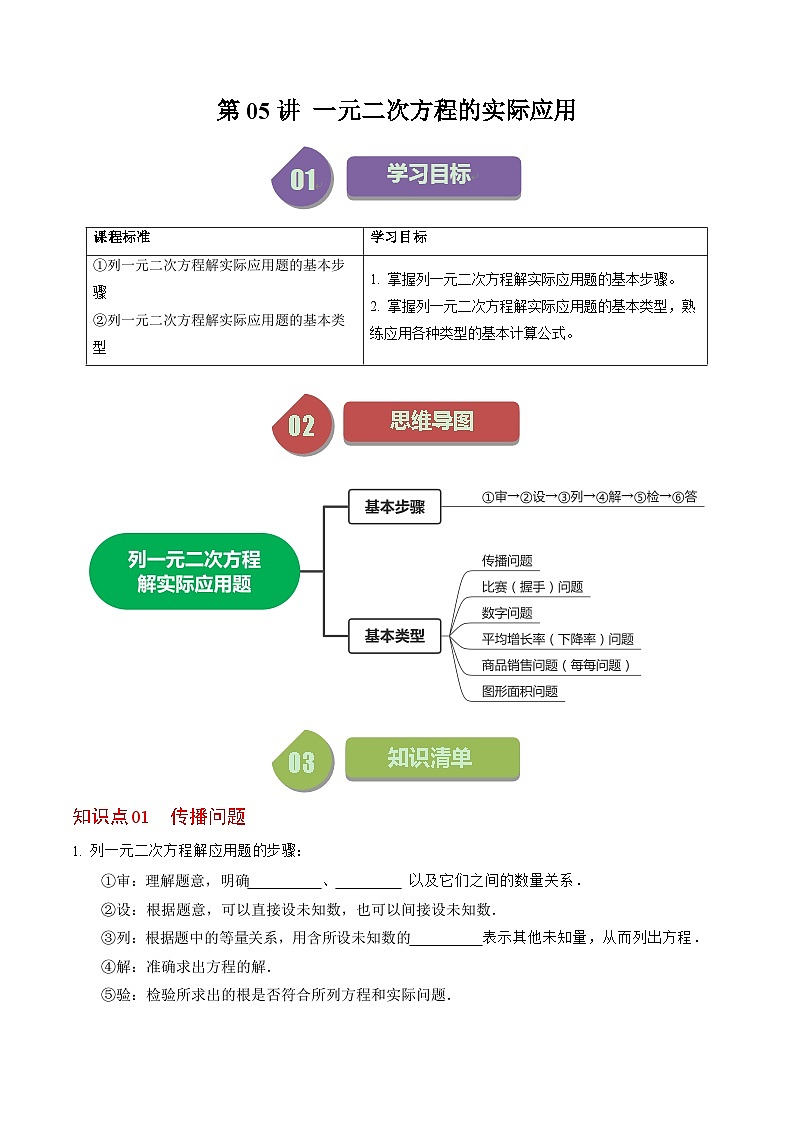
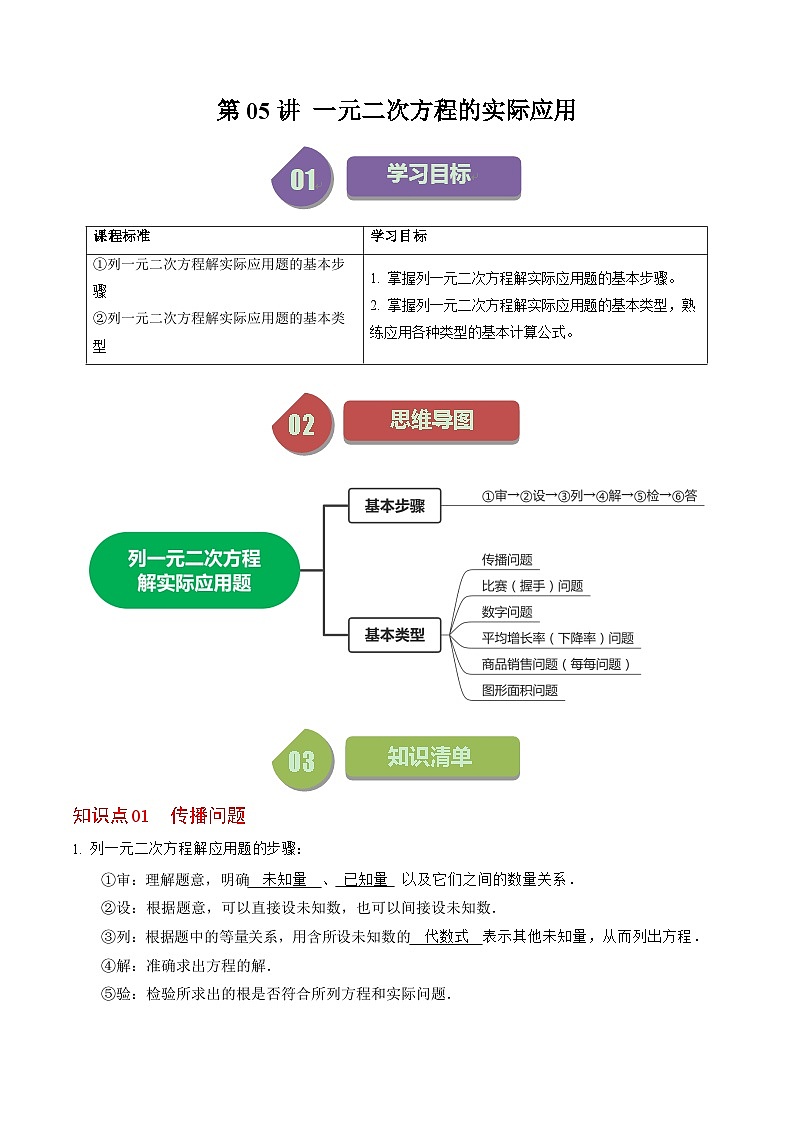
知识点01 传播问题
列一元二次方程解应用题的步骤：
①审：理解题意，明确 未知量 、 已知量 以及它们之间的数量关系．
②设：根据题意，可以直接设未知数，也可以间接设未知数．
③列：根据题中的等量关系，用含所设未知数的 代数式 表示其他未知量，从而列出方程．
④解：准确求出方程的解．
⑤验：检验所求出的根是否符合所列方程和实际问题．
⑥答：写出答案。
传播问题：
计算公式： 。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
1．进入2022年秋冬季以来，全国疫情呈现多点爆发，感染人数急速增长的新趋势，而此次疫情主要由奥密克戎变异株引起．据调查，奥密克戎变异株的主要特点是致病性减弱，但传播速度更快，传染性更强．在对该病毒的流行性病学调查中发现，在不加任何防护措施的情况下，若1人患病，经过两轮感染后患病人数竟高达324人，则每轮感染中，1个人会平均感染多少人？若设每轮感染中，1个人会平均感染x个人，则下列方程正确的是（ ）
A．1+x+x2＝324B．（1+x）2＝324
C．1+x+（1+x）2＝324D．x+（1+x）2＝324
【解答】解：设每轮感染中，1个人会平均感染x个人，
则两轮感染后的总人数为：（1+x）2＝324．
故选：B．
【即学即练2】
2．春节过后，甲型流感病毒（以下简称：甲流）开始悄然传播，某办公室最初有三人同时患上甲流，经过两轮传播后，办公室现有27人确诊甲流，请问在两轮传染过程中，平均一人会传染给几个人？
【解答】解：设在两轮传染过程中，平均一人会传染给x个人，则第一轮传染中有3x人被传染，第二轮传染中有（3+3x）x人被传染，
根据题意得：3+3x+（3+3x）x＝27，
整理得：（1+x）2＝9，
解得：x1＝2，x2＝﹣4（不符合题意，舍去）．
答：在两轮传染过程中，平均一人会传染给2个人．
知识点02 比赛（握手）问题
比赛（握手）问题：
计算公式：单循环（两两之间比赛（握手）一次）： 。
双循环（两两之间比赛（握手）两次）： 。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
3．某乒乓球比赛的每两队之间都进行1场比赛，共要比赛28场，设共有x支球队参加该比赛，则符合题意的方程是（ ）
A．x2＝28B．x2＝28×2
C．D．x（x﹣1）＝28×2
【解答】解：根据题意得，
即x（x﹣1）＝28×2，
故选：D．
【即学即练2】
4．某校要组织一场篮球联赛，每两队之间都赛2场（双循环），计划安排30场比赛，设有x支球队，可列方程为（ ）
A．x（x+1）＝60B．x（x﹣1）＝30C．x（x+1）＝15D．x（x﹣1）＝60
【解答】解：设有x支球队，每两队之间都赛2场（双循环），计划安排30场比赛，
∴x（x﹣1）＝30，
故选：B．
【即学即练3】
5．某校九年级学生毕业时，每个同学都将自己的相片向全班其他同学各送一张留作纪念，全班共送了1640张相片，全班有多少名学生？
【解答】解：设全班有x名学生，根据题意得：
x（x﹣1）＝1640，
解得x＝﹣40（舍去）或x＝41，
答：全班有41名学生．
【即学即练4】
6．为增强学生身体素质，提高学生足球运动竞技水平，某市开展“希望杯”足球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应邀请多少个球队参赛？
【解答】解：设：应该邀请x个球队参加，
由题意得：x（x﹣1）＝21，
解得：x＝7或x＝﹣6（舍去），
答：应邀请7个球队参赛．
知识点03 数字问题
数字问题：
数字问题：个位数为a，十位数是b，则这个两位数表示为 10b+a 。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
7．读诗词，列方程：大江东去浪淘尽，千古风流人物；而立之年督东吴，早逝英年两位数，十位恰小个位三，个位平方与寿符．（诗词大意：周瑜英年早逝，逝世时的年龄是一个两位数，十位数字比个位数字小3，个位数字的平方刚好是周瑜逝世时的年龄），设周瑜逝世时的年龄的个位数字为x，则列出的方程正确的是（ ）
A．10x+（x﹣3）＝x2B．10（x﹣3）+x＝x2
C．10x+（x﹣3）＝（x﹣3）2D．10（x﹣3）+x＝（x﹣3）2
【解答】解：∵周瑜逝世时的年龄的个位数字为x，且十位数字比个位数字小3，
∴周瑜逝世时的年龄的十位数字为（x﹣3）．
根据题意得：10（x﹣3）+x＝x2．
故选：B．
【即学即练2】
8．一个两位数，十位上的数字比个位上的数字的平方小9，如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，求原来的两位数．
【解答】解：设原两位数个位上的数字为x，则十位上的数字为（x2﹣9）．
∴10（x2﹣9）+x﹣10x﹣（x2﹣9）＝27，
解得x1＝4，x2＝﹣3（不符合题意，舍去）．
∴x2﹣9＝7，
∴10（x2﹣9）+x＝74．
答：原两位数为74．
知识点04 平均增长率（下降率）问题
平均增长率（下降率）问题：
计算公式：平均增长类型： 。
平均下降类型： 。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
9．根据福建省统计局数据，福建省2020年的地区生产总值为43903.89亿元，2022年的地区生产总值为53109.85亿元．设这两年福建省地区生产总值的年平均增长率为x，根据题意可列方程（ ）
A．43903.89（1+x）＝53109.85
B．43903.89（1+x）2＝53109.85
C．43903.89x2＝53109.85
D．43903.89（1+x2）＝53109.85
【解答】解：设这两年福建省地区生产总值的年平均增长率为x，
根据题意得，43903.89（1+x）2＝53109.85，
故选：B．
【即学即练2】
随旅游旺季的到来，某景区游客人数逐月增加，2月份游客人数为1.6万人，4月份游客人数为2.5万人．
（1）求这两个月中该景区游客人数的月平均增长率；
（2）预计5月份该景区游客人数会继续增长，但增长率不会超过前两个月的月平均增长率．已知该景区5月1日至5月21日已接待游客2.125万人，则5月份后10天日均接待游客人数最多是多少万人？
【解答】解：（1）设这两个月中该景区游客人数的月平均增长率为x，
由题意可得：1.6（1+x）2＝2.5，
解得：x＝25%，x＝﹣（不合题意舍去），
答：这两个月中该景区游客人数的月平均增长率为25%；
（2）设5月份后10天日均接待游客人数是a万人，
由题意可得：2.125+a≤2.5（1+25%），
解得：a≤1，
答：5月份后10天日均接待游客人数最多是1万人．
知识点05 商品销售问题（每每问题）
商品销售问题（每每问题）：
计算公式：总利润＝ 单利润×数量
现单利＝ 原单利＋涨价部分（原单利－降价部分）
现数量＝ 原数量－（原数量＋）
特别说明：题目中出现的价格每上涨（下降）a数量会变化b，其中a为涨价（降价）基础，b为变化基数。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
11．某商场销售一款T恤，进价为每件40元，当售价为每件60元时，平均每周可卖出200件，为扩大销售，增加利润，商场准备降价销售．经市场调查发现，每件每降价1元，平均每周可多卖出8件，若要使每周销售该款T恤获利8450元，设每件降低x元，则可列方程为（ ）
A．（60﹣x）（200+8x）＝8450B．（20﹣x）（200+x）＝8450
C．（40﹣x）（200+8x）＝8450D．（20﹣x）（200+8x）＝8450
【解答】解：当每件降低x元时，每件的销售利润为60﹣x﹣40＝（20﹣x）元，平均每周可售出（200+8x）件，
根据题意得：（20﹣x）（200+8x）＝8450．
故选：D．
【即学即练2】
12．世界读书日是在每年的4月23日，“世界图书日”设立目的是推动更多的人去阅读和写作，希望所有人都能尊重和感谢为人类文明做出过巨大贡献的文学、文化、科学、思想大师们，保护知识产权．某批发商在世界读书日前夕，订购了一批具有纪念意义的书签进行销售，平均每天可售出500张，每张可获利0.5元．调查发现，如果每张书签的售价每降价0.1元，平均每天可多售出200张．批发商要想平均每天获利270元，求每张书签应降价多少元．
【解答】解：设每张书签应降价x元，则每张的销售利润为（0.5﹣x）元，平均每天可售出（500+×200）张，
根据题意得：（0.5﹣x）（500+×200）＝270，
整理得：100x2﹣25x+1＝0，
解得：x1＝0.2，x1＝0.05．
答：每张书签应降价0.2元或0.05元．
知识点06 图形面积问题
图形面积问题：
①利用勾股定理列一元二次方程，求三角形、矩形的边长．
②利用三角形、矩形、菱形、梯形和圆的面积，以及柱体体积公式建立等量关系列一元二次方程。
题型考点：①根据解题步骤把实际问题抽象出一元二次方程。②根据解题步骤列方程解决实际问题。
【即学即练1】
13．如图，某校生物兴趣小组用长为18米的篱笆，一面利用墙（墙的长度足够），围成中间隔有一道篱笆的长方形花圃ABCD，为了方便出入，建造篱笆花圃时在BC边留了宽为1米的两个进出口（不需材料），若花圃的面积刚好为40平方米，设AB的长为x米，则可列方程为（ ）
A．x（18﹣3x）＝40B．x（20﹣2x）＝40
C．x（22﹣3x）＝40D．x（20﹣3x）＝40
【解答】解：∵篱笆的总长为18米，AB的长为x米，
∴BC的长为18+2﹣3x＝（20﹣3x）米．
根据题意得：x（20﹣3x）＝40．
故选：D．
【即学即练2】
14．如图，某学校有一块长30m，宽10m的长方形空地，计划在其中修建两块相同的长方形绿地，两块绿地之间及周边留有宽度相等的人行通道．若两块长方形绿地的面积共216m2，求人行通道的宽度．
【解答】解：设人行通道的宽度为x米，则两块长方形绿地可合成长为（30﹣3x）米，宽为（10﹣2x）米的长方形，
根据题意得：（30﹣3x）（10﹣2x）＝216，
整理得：x2﹣15+14＝0，
即（x﹣1）（x﹣14）＝0，
解得：x1＝1，x2＝14，
当x＝14时，30﹣3x＝30﹣3×14＝﹣12＜0，不符合题意，舍去，
∴x＝1．
答：人行通道的宽度是1米．
题型01 商品销售问题（每每问题）
【典例1】
服装批发市场有一批服装，如果每件盈利50元，每天可售出500件．经市场调查发现，在进货价不变的情况下，若每件涨价1元，日销量将减少2件．
（1）若以每件能盈利70元的单价出售，每天的总利润为多少元？
（2）现市场要保证每天总利润40000元，同时又要使顾客得到实惠，则每件应涨价多少元？
【解答】解：（1）70×（500﹣40）＝32200（元），
（2）设涨价x元，
（50+x）（500﹣2x）＝40000，
解得x1＝150，x2＝50，
为了让顾客得到实惠，
∴x＝50，涨价50元．
答：每千克应涨价50元．
【典例2】
“早黑宝”葡萄品种是山西省农科院研制的优质新品种，在山西省被广泛种植．某市某葡萄种植基地到2018年年底已经种植“早黑宝”100亩，到2020年年底“早黑宝”的种植面积达到196亩．
（1）求该基地这两年“早黑宝”种植面积的年平均增长率；
（2）市场调查发现，当“早黑宝”的售价为20元/千克时，每天能售出200千克，销售单价每降低1元，每天可多售出50千克，为了减少库存，该基地决定降价促销．已知该基地“早黑宝”的平均成本为12元/千克，若使销售“早黑宝”每天可获利1750元，则销售单价应降低多少元？
【解答】（1）设该基地这两年“早黑宝”种植面积的平均增长率为x，根据题意得
100（1+x）2＝196，
解得x1＝0.4＝40%，x2＝﹣2.4（不合题意，舍去），
答：该基地这两年“早黑宝”种植面积的平均增长率为40%．
（2）设售价应降低y元，则每天可售出（200+50y）千克，
根据题意，得（20﹣12﹣y）（200+50y）＝1750，
整理得，y2﹣4y+3＝0，
解得y1＝1，y2＝3，
∵要减少库存，
∴y1＝1不合题意，舍去，
∴y＝3．
答：售价应降低3元．
【典例3】
4月10﹣13日习近平总书记在广东考察时强调：推进中国式现代化，必须全面推进乡村振兴，解决好城乡区域发展不平衡问题，产业振兴是乡村报兴的重中之重，要落实产业帮扶致策，做好“土特产”文章，网络直播带货助力乡村振兴，它作为一种新颖的销售“土特产”的方式，受到社会各界的追捧，某直播间销售某种“土特产”，每袋获利40元，每天可卖出20袋，通过市场调查发现：每袋“土特产”的售价每降低1元，每天的销售量就增加2袋．
（1）若每袋“土特产”的售价降低6元，求每天的销售量．
（2）为尽快减少库存，商家决定降价销售，若要使得每天获利1200元，则每袋“土特产”的售价降低了多少元？
【解答】解：（1）20+2×6
＝20+12
＝32（袋）．
答：每天的销售为32袋；
（2）设每袋“土特产”的售价降低了x元，则每袋“土特产”的销售利润为（40﹣x）元，每天可售出（20+2x）袋，
根据题意得：（40﹣x）（20+2x）＝1200，
整理得：x2﹣30x+200＝0，
解得：x1＝10，x2＝20，
又∵要尽快减少库存，
∴x＝20．
答：每袋“土特产”的售价降低了20元．
1．新冠肺炎具有人传人的特性，若一人携带病毒未进行有效隔离，经过两轮传染后共有256人患新冠肺炎，设每轮传染中平均每个人传染了x人，则根据题意可列出方程（ ）
A．x（1+x）＝256B．x+（1+x）2＝256
C．x+x（1+x）＝256D．1+x+x（1+x）＝256
【解答】解：每轮传染中平均每个人传染了x人，根据题意可列出方程，1+x+x（1+x）＝256，
故选：D．
2．2023年某电影上映的第一天票房为2亿元，第二天、第三天单日票房持续增长，三天累计票房为6.62亿元，若第二天、第三天单日票房按相同的增长率增长，设平均每天票房的增长率为x，则根据题意，下列方程正确的是（ ）
A．2（1+x）＝6.62
B．2（1+x）2＝6.22
C．2（1+x）+2（1+x）2＝6.62
D．2+2（1+x）+2（1+x）2＝6.62
【解答】解：∵某电影上映的第一天票房为2亿元，且平均每天票房的增长率为x，
∴该电影上映的第二天票房为2（1+x）亿元，第三天票房为2（1+x）2亿元．
根据题意得：2+2（1+x）+2（1+x）2＝6.62．
故选：D．
3．为大力实施城市绿化行动，某小区规划设置一片面积为1000平方米的矩形绿地，并且长比宽多30米，设绿地长为x米，根据题意可列方程为（ ）
A．x（x+30）＝1000B．x（x﹣30）＝1000
C．2x（x+30）＝1000D．2x（x﹣30）＝1000
【解答】解：设绿地长为x米，则宽为（x﹣30）米，根据题意得：
x（x﹣30）＝1000，故B正确．
故选：B．
4．为丰富乡村文体生活，某区准备组织首届“美丽乡村”篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，设邀请x个球队参加比赛，可列方程得（ ）
A．B．
C．x（x﹣1）＝28D．x（x+1）＝28
【解答】解：根据题意得：x（x﹣1）＝28．
故选：A．
5．某商品的进价为每件40元，当售价为每件60元时，每星期可卖出200件，现需降价处理，且经市场调查发现：每降价1元，每星期可多卖出8件，店里每周利润要达到8450元．若设店主把该商品每件售价降低x元，则可列方程为（ ）
A．（60﹣x）（200+8x）＝8450B．（20﹣x）（200+x）＝8450
C．（20﹣x）（200+40x）＝8450D．（20﹣x）（200+8x）＝8450
【解答】解：当店主把该商品每件售价降低x元时，每件的销售利润为60﹣x﹣40＝（20﹣x）元，每星期可卖出（200+8x）件，
根据题意得：（20﹣x）（200+8x）＝8450．
故选：D．
6．一个两位数的两个数字的和为9，把这个两位数的个位数字与十位数字互换得到一个新的两位数，它与原两位数的积为1458，设原两位数的个位数字为x，则可列方程（ ）
A．[（9﹣x）+x][10x+（9﹣x）]＝1458
B．[（9﹣x）+x][x+（9﹣x）]＝1458
C．[10（9﹣x）+x][10x+（9﹣x）]＝1458
D．[10（9﹣x）+x][x+（9﹣x]＝1458
【解答】解：设个位数字为x，则十位数字为（9﹣x），
根据题意得：[10x+（9﹣x）][10（9﹣x）+x]＝1458，
故选：C．
7．如果不防范，病毒的传播速度往往很快，有一种病毒1人感染后，经过两轮传播，共有361人感染．
（1）平均每人每轮感染多少人？
（2）第二轮传播后，人们加强防范，使病毒的传播力度减少到原来的a%，这样第三轮传播后感染的人数只是第二轮传播后感染人数的10倍，求a的值．
【解答】解：（1）设平均每人每轮感染x人，
由题意得：1+x+x（x+1）＝361，
解得：x1＝18，x2＝﹣20（不符合题意，舍去），
答：平均每人每轮感染18人；
（2）由题意得：361+361×18×a%＝10×361，
解得：a＝50，
答：a的值为50．
8．2022年北京冬奥会冰壶混双项目在国家游泳中心“冰立方”开赛，中国混双球队参加了比赛，赛制为单循环比赛（每两队之间都赛一场）．
（1）如果有6支球队参加比赛，那么共进行 场比赛；
（2）如果一共进行45场比赛，那么有多少支球队参加比赛？
【解答】解：（1）6×（6﹣1）÷2＝15（场），
∴如果有6支球队参加比赛，那么共进行15场比赛．
故答案为：15．
（2）设有x支球队参加比赛，
根据题意得：x（x﹣1）＝45，
整理得：x2﹣x﹣90＝0，
解得：x1＝10，x2＝﹣9（不符合题意，舍去）．
答：有10支球队参加比赛．
9．阅读材料，回答下列问题：
反序数：
有这样一对数，一个数的数字排列完全颠倒过来变成另一个数，简单的说，就是顺序相反的两个数，我们把这样的一对数称为“反序数”，比如：12的反序数是21，456的反序数是654．
用方程知识解决问题：
若一个两位数，其十位上的数字比个位上的数字大3，这个两位数与其反序数之积为1300，求这个两位数．
【解答】解：设这个两位数的个位数字为x，则十位数字为（x+3），
根据题意得：[10（x+3）+x]（10x+x+3）＝1300，
整理得：x2+3x﹣10＝0，
解得：x1＝﹣5（不符合题意，舍去），x2＝2，
∴10（x+3）+x＝10×（2+3）+2＝52．
答：这个两位数为52．
10．为响应国家全民阅读的号召，社区鼓励居民到社区阅览借阅读书，并统计每年的借阅人数和图书借阅总量（单位：本）．该阅览室在2017年图书借阅总量是7500本，2019年图书借阅总量是10800本．
（1）求该社区的图书借阅总量从2017年至2019年的年平均增长率；
（2）如果每年的增长率相同，预计2020年图书借阅总量是多少本．
【解答】解：（1）设该社区的图书借阅总量从2017年至2019年的年平均增长率为x，
根据题意得：7500（1+x）2＝10800，
解得：x1＝0.2＝20%，x2＝﹣2.2（不符合题意，舍去）．
答：该社区的图书借阅总量从2017年至2019年的年平均增长率为20%；
（2）10800×（1+20%）
＝10800×1.2
＝12960（本）．
答：如果每年的增长率相同，预计2020年图书借阅总量是12960本．
11．2023亚洲花卉产业博览会于2023年5月10至12日，在中国进出口交易会展馆举办，为了迎接盛会的到来，组委会想利用一块长方形空地建了一个小型的惠民停车场，其布局如图所示，已知停车场的长为52m，宽为28m，阴影部分设计为停车位，其余部分是等宽的通道，已知停车位占地面积为640m2．求通道的宽是多少米？
【解答】解：设通道的宽是x米，则停车位部分可合成长为（52﹣2x）米，宽为（28﹣2x）米的长方形，
根据题意得：（52﹣2x）（28﹣2x）＝640，
整理得：x2﹣40x+204＝0，
解得：x1＝6，x2＝34（不符合题意，舍去）．
答：通道的宽是6米．
12．2018﹣2020年注定是不平凡的三年，2018年非洲猪瘟疫情爆发，2019年中国猪肉价格持续高涨，2020年新冠病毒爆发，目前各行各业都存在潜在的变化，例如2019年猪肉价格持续高涨，引起了政府、市场监督等部门的高度重视，据统计，2019年1月精品瘦肉的售价为32元/千克，由于猪瘟疫情，生猪减少，市场对猪肉的需求量持续增加，所以猪肉价格持续上涨，已知2020年1月猪肉的售价比2019年1月上涨了5a%，市民王大爷2020年1月18号在双福镇永辉超市购买4.5千克的精品瘦肉花了324元．
（1）求a的值；
（2）双福镇永辉超市将进价为52元/千克的精品瘦肉，按2020年1月18号的价格出售，平均每天能售出150千克，因为政府部门的高度重视，猪肉价格有所下降，经市场调查发现，精品瘦肉的售价每千克下降1元，其日销量就增加10千克，双福镇永辉超市为实现销售精品瘦肉每天有3040元的利润，并尽可能让消费者得到实惠，精品瘦肉的售价应为多少元？
【解答】解：（1）根据题意得：
32×（1+5a%）×4.5＝324，
解得a＝25，
∴a的值为25；
（2）设精品瘦肉的售价应为x元，
2020年1月18号的价格为32×（1+）＝72（元/千克），
根据题意得：（x﹣52）[150+10×（72﹣x）]＝3040，
解得x＝71或x＝68，
∵尽可能让消费者得到实惠，
∴x取68，
答：精品瘦肉的售价应为每千克68元．
课程标准
学习目标
①列一元二次方程解实际应用题的基本步骤
②列一元二次方程解实际应用题的基本类型
掌握列一元二次方程解实际应用题的基本步骤。
掌握列一元二次方程解实际应用题的基本类型，熟练应用各种类型的基本计算公式。