初中数学2 不等式的基本性质图文ppt课件

展开

这是一份初中数学2 不等式的基本性质图文ppt课件，共24页。PPT课件主要包含了学习目标，情境导入，符号语言，探究新知，不等式的性质，举例一，举例二，归纳总结，不等号的方向不变，不等号的方向改变等内容，欢迎下载使用。

1. 经历不等式的基本性质的探索过程，初步体会不等式和等式的异同；2. 掌握不等式的基本性质，并能初步运用不等式的基本性质把比较简单的不等式转化成“x>a”或“x你还记得等式的基本性质吗？
等式的基本性质1：在等式的两边都加（或减）同一个数或整式，所得结果仍是等式.
如果a=b，那么a+c=b+c，a-c=b-c
等式的基本性质2：在等式的两边都乘（或除以）同一个数（除数不为0），所得结果仍是等式.
不等式与等式只有一字之差，那么它们的性质是否也有相似之处呢？
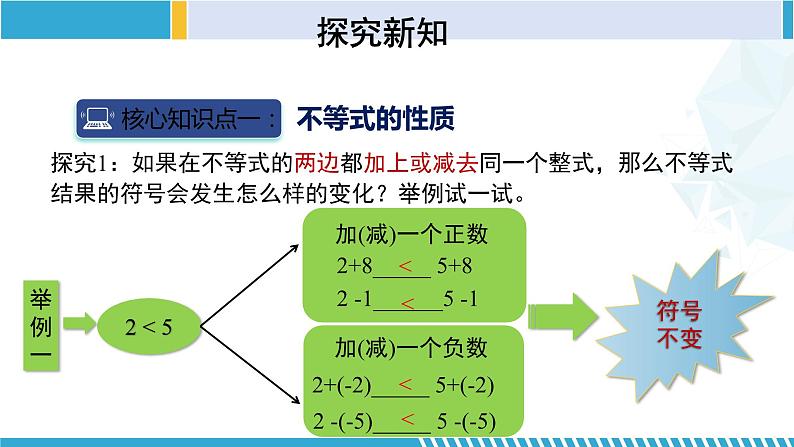
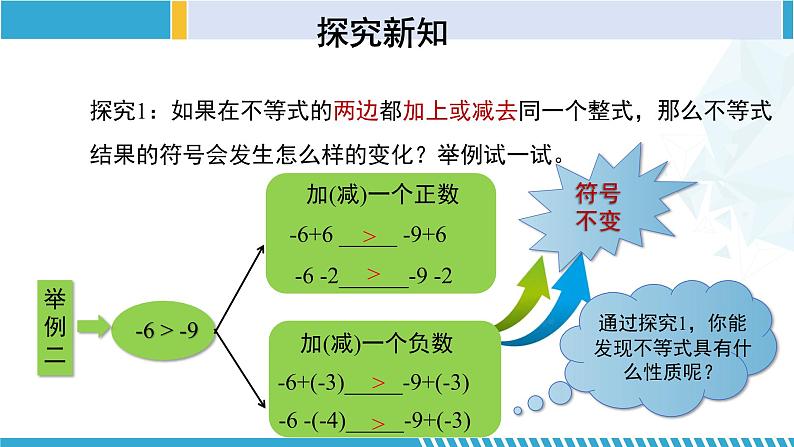
探究1：如果在不等式的两边都加上或减去同一个整式，那么不等式结果的符号会发生怎么样的变化？举例试一试。
不等式的基本性质1：不等式的两边都加（或减）同一个整式，不等号的方向不变．
用字母表示：若a＞b，则a＋c ＞b＋c（或a－c ＞b－c）.
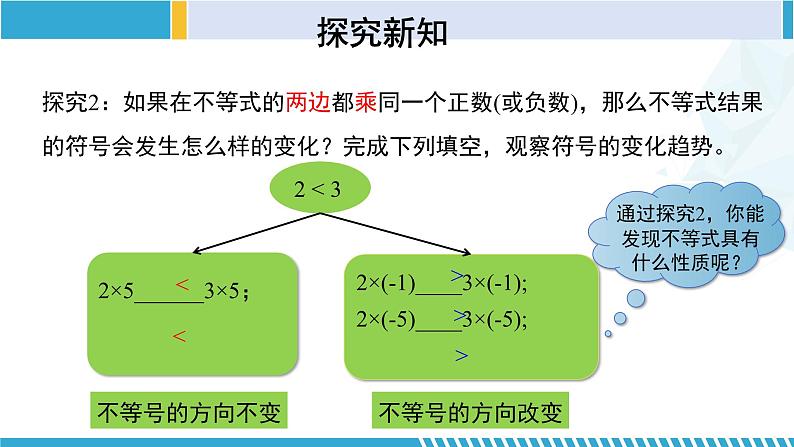
探究2：如果在不等式的两边都乘同一个正数(或负数)，那么不等式结果的符号会发生怎么样的变化？完成下列填空，观察符号的变化趋势。
探究3：如果在不等式的两边都除以同一个正数(或负数)，那么不等式结果的符号会发生怎么样的变化？完成下列填空，观察符号的变化趋势。
不等式的基本性质2 不等式两边都乘（或除以）同一个正数，不等号的方向不变.
不等式的基本性质3：不等式的两边都乘（或除以）同一个负数，不等号的方向改变．
（1） a - 3____b - 3；（2） a÷3____b÷3（3） ; （4） -4a____-4b（5） 2a+3____2b+3;（6）(m2+1)a____ (m2+1)b(m为常数)
设a＞b，用“＜”“＞”填空并回答是根据不等式的哪一条基本性质.
利用不等式的性质把不等式化成x＞a、x＜a的形式
例：将下列不等式化成“x＞a”或“x＜a”的形式．
解：（1）根据不等式的基本性质1，两边都加5，得
（2）根据不等式的基本性质3，两边都除以-2，得
(3)不等式两边同时减去4x得 5x-4x <4x-8-4x, 即x <-8.
注意：当不等式两边都乘以（或除以）同一个数时，一定要看清是正数还是负数；对于未给定范围的字母，应分情况讨论。
1、已知a，b，c均为实数，a0 B. -3a<-3bC. a|c|2.如果m>n，那么下列结论错误的是（） A．m+2>n+2 B．m-2>n-2 C．2m>2n D．-2m>-2n
4.若 x＜y，比较2-3x与2-3y的大小，则下列选项正确的是（） A. 2-3x>2-3y B .2-3x<2-3y C. 2-3x=2-3y D. 无法比较大小
5.若 3x>-3y，则下列一定成立的是（） A. x+y>0 B .x-y>0 C.x+y<0 D. x-y<0
6.比较大小：(1)如果a－1＞b＋2，那么a________b.(2)试比较2a与3a的大小：①当a＞0时，2a________3a；②当a＝0时，2a________3a；③当a＜0时，2a________3a.
7.判断下列各题的推导是否正确？并说明理由.(1)因为a+8＞4，所以a＞-4；(2)因为4a＞4b，所以a＞b；(3)因为3＞2，所以3a＞2a．
正确，根据不等式基本性质1．
正确，根据不等式基本性质2．
不对，应分情况逐一讨论． a＞0，a=0，a＜0.
8.试比较a＋b与a的大小．9.试判断x2－3x＋1与－3x＋1的大小．
解：∵x2≥0， ∴x2－3x＋1≥－3x＋1.
解：当b＞0时，a＋b＞a；当b＝0时，a＋b＝a；当b＜0时，a＋b＜a.
10．根据不等式的性质，把下列不等式化成x＞a或x＜a的形式．（1）x+7＞9；（2）6x＜5x﹣3；（3）
利用不等式的性质把不等式化成“x>a”或“x不等式的基本性质1：不等式的两边都加 (或减) 同一个整式，不等号的方向不变
不等式的基本性质2：不等式的两边都乘（或除以）同一个正数，不等号的方向不变
不等式基本性质3：不等式的两边都乘（或除以）同一个负数，不等号的方向改变

相关课件更多