初中数学沪教版 (五四制)八年级下册22.3 特殊的平行四边形当堂达标检测题

这是一份初中数学沪教版 (五四制)八年级下册22.3 特殊的平行四边形当堂达标检测题，文件包含2233正方形的性质与判定原卷版docx、2233正方形的性质与判定解析版docx等2份试卷配套教学资源，其中试卷共69页， 欢迎下载使用。
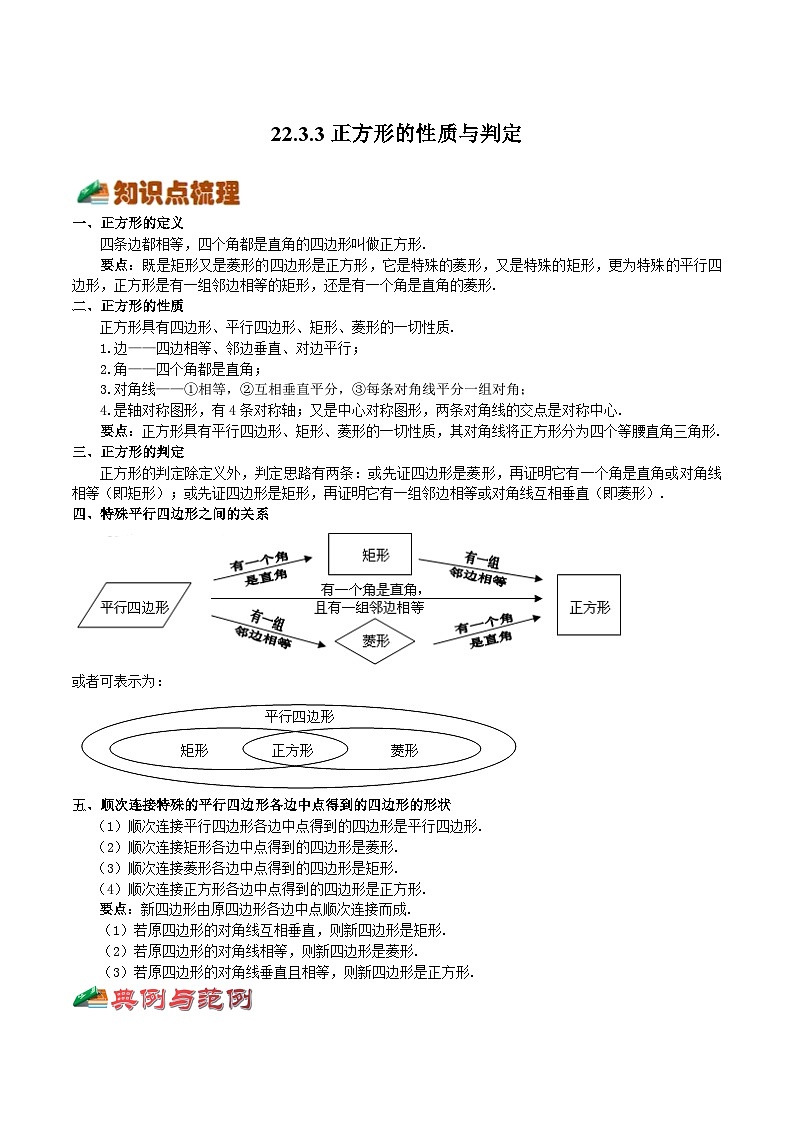
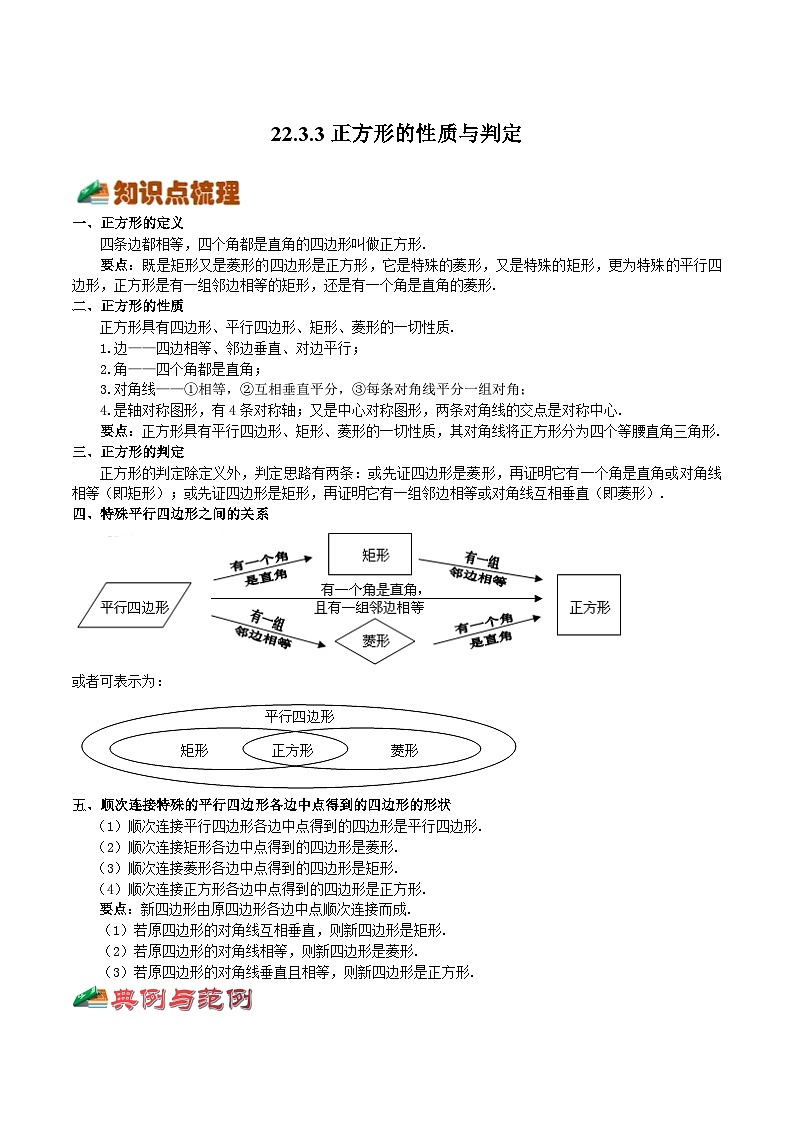
一、正方形的定义
四条边都相等，四个角都是直角的四边形叫做正方形.
要点：既是矩形又是菱形的四边形是正方形，它是特殊的菱形，又是特殊的矩形，更为特殊的平行四边形，正方形是有一组邻边相等的矩形，还是有一个角是直角的菱形.
二、正方形的性质
正方形具有四边形、平行四边形、矩形、菱形的一切性质.
1.边——四边相等、邻边垂直、对边平行；
2.角——四个角都是直角；
3.对角线——①相等，②互相垂直平分，③每条对角线平分一组对角；
4.是轴对称图形，有4条对称轴；又是中心对称图形，两条对角线的交点是对称中心.
要点：正方形具有平行四边形、矩形、菱形的一切性质，其对角线将正方形分为四个等腰直角三角形.
三、正方形的判定
正方形的判定除定义外，判定思路有两条：或先证四边形是菱形，再证明它有一个角是直角或对角线相等（即矩形）；或先证四边形是矩形，再证明它有一组邻边相等或对角线互相垂直（即菱形）.
四、特殊平行四边形之间的关系
或者可表示为：
五、顺次连接特殊的平行四边形各边中点得到的四边形的形状
（1）顺次连接平行四边形各边中点得到的四边形是平行四边形.
（2）顺次连接矩形各边中点得到的四边形是菱形.
（3）顺次连接菱形各边中点得到的四边形是矩形.
（4）顺次连接正方形各边中点得到的四边形是正方形.
要点：新四边形由原四边形各边中点顺次连接而成.
（1）若原四边形的对角线互相垂直，则新四边形是矩形.
（2）若原四边形的对角线相等，则新四边形是菱形.
（3）若原四边形的对角线垂直且相等，则新四边形是正方形.
题型1：正方形的性质
1．正方形、矩形、菱形都具有的特征是（ ）
A．对角线互相平分B．对角线相等
C．对角线互相垂直D．对角线平分一组对角
2．正方形具有而菱形不一定有的性质是（ ）
A．对角线相等B．对角线互相垂直
C．对角相等D．四条边相等
题型2：利用正方形的性质求长度
3．正方形一条对角线长为，则周长为（ ）
A．4B．C．8D．
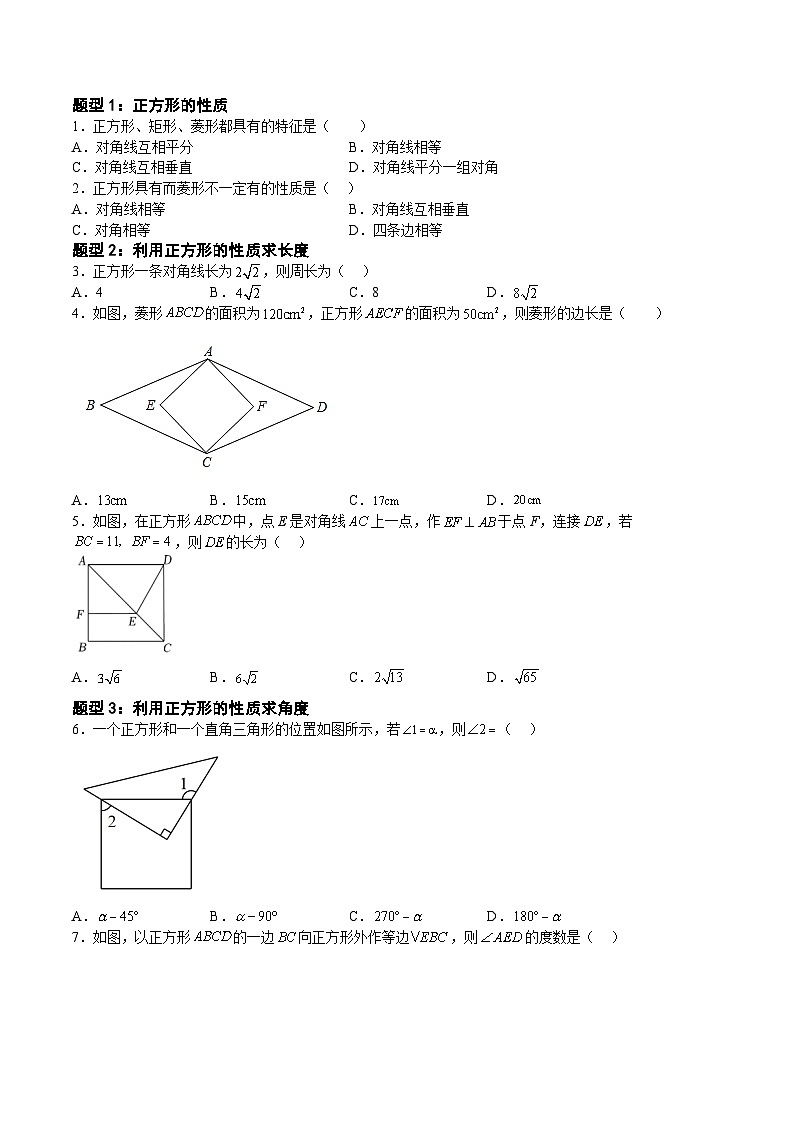
4．如图，菱形的面积为，正方形的面积为，则菱形的边长是（ ）
A．B．C．D．
5．如图，在正方形中，点E是对角线上一点，作于点F，连接，若，则的长为（ ）
A．B．C．D．
题型3：利用正方形的性质求角度
6．一个正方形和一个直角三角形的位置如图所示，若，则（ ）
A．B．C．D．
7．如图，以正方形的一边向正方形外作等边，则的度数是（ ）
A．B．C．D．
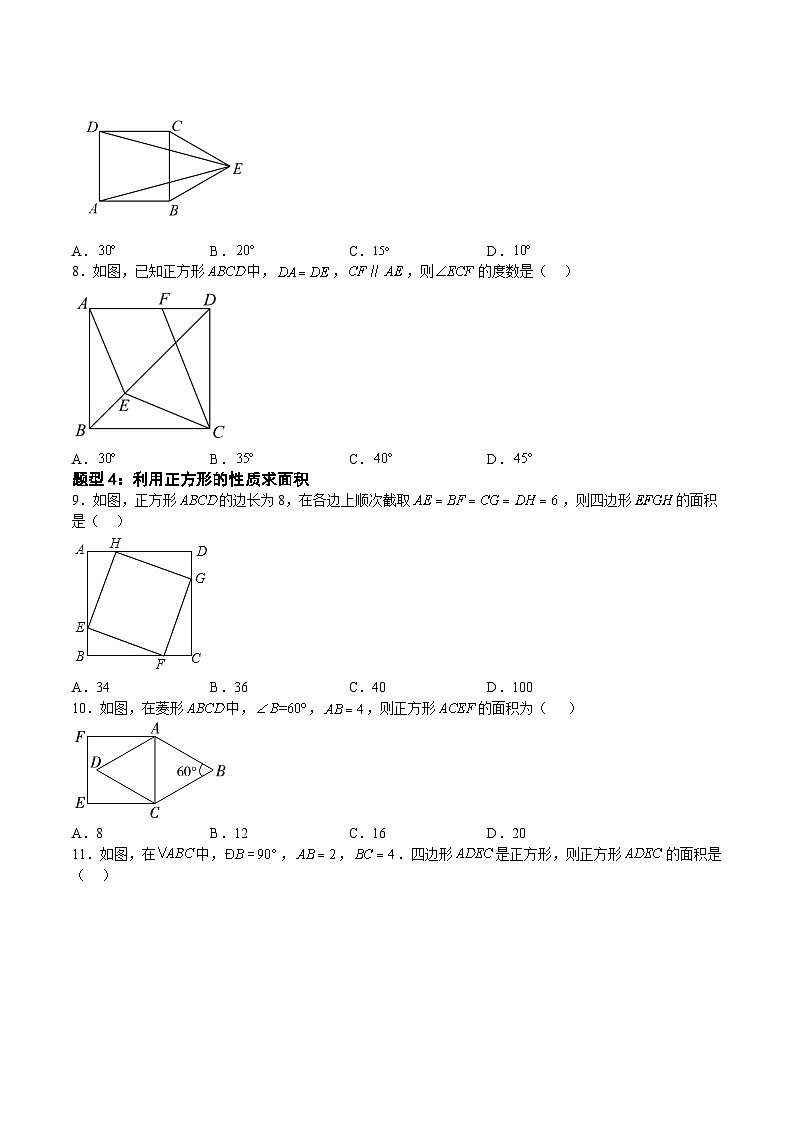
8．如图，已知正方形中，，，则的度数是（ ）
A．B．C．D．
题型4：利用正方形的性质求面积
9．如图，正方形的边长为8，在各边上顺次截取，则四边形的面积是（ ）
A．34B．36C．40D．100
10．如图，在菱形中，，，则正方形的面积为（ ）
A．8B．12C．16D．20
11．如图，在中，，，．四边形是正方形，则正方形的面积是（ ）
A．8B．12C．18D．20
12．如图将边长为的大正方形与边长为的小正方形放在一起，则三角形的面积（ ）
A．与、大小都有关B．与、的大小都无关
C．只与的大小有关D．只与的大小有关
题型5：正方形的判定
13．如图，在矩形中，对角线交于点O，下列条件中，能使矩形成为正方形的是（ ）
A． B．C．D．
14．有下列四个条件：①；②；③；④；从中选两个作为补充条件，使平行四边形为正方形，现有下列四种选法，你认为错误的是（ ）
A．①②B．①③C．②③D．②④
题型6：中点四边形
15．连接菱形各边中点，可得到的“中点四边形”是矩形，主要是因为（ ）
A．菱形的四条边都相等B．菱形的对角线互相垂直
C．菱形的对角线互相平分D．以上答案都不对
16．如图，AC、BD是四边形ABCD的两条对角线，顺次连接四边形ABCD各边中点得到四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）
A．AC⊥BDB．AB＝CDC．AB∥CDD．AC＝BD
17．若顺次联结一个四边形各边的中点得到的图形是矩形，则这个四边形的对角线（ ）
A．互相平分B．相等C．互相垂直D．互相垂直且平分
题型7：正方形的判定与性质综合
18．如图，点E是正方形对角线上一点，过E作交于F，连接，若，，则的长为（ ）
A．B．C．D．
19．如图，正方形的边长为，为边上一点与点、不重合，连接，交于点当是等腰三角形时，则的长为（ ）
A．
B．
C．
D．
20．如图，正方形ABCD边长为10，点M在对角线AC上运动，N为DC上一点，DN＝2，则DM+ MN长的最小值为（ ）
A．8B．10C．D．
21．如图，ABCD为正方形，O为AC、BD的交点，△DCE为Rt△，∠CED=90°，∠DCE=30°，若OE=，则正方形的面积为（ ）
A．5B．4C．3D．2
22．ABCD是边长为1的正方形，是等边三角形，则的面积为
A．
B．
C．
D．
题型8：正方形的判定与性质解答题
23．如图，若四边形的对角线与相交于点O，且，则四边形是正方形吗？
24．如图，M、N分别是正方形的边的中点，与交于点P，连结，求证：．
25．如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
（1）求证：CE=CF；
（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
26．如图，E，F是正方形ABCD的对角线BD上的两点，且BE＝DF．
(1)求证：△ABE≌△CDF；
(2)若AB＝3，BE＝2，求四边形AECF的面积．
27．如图，正方形ABCD中，．
(1)求证：；
(2)求证：；
(3)若，且，则_______．
一、单选题
1．正方形具有而矩形不一定具有的性质是（ ）
A．四个角都相等B．对角线互相平分C．对角线相等D．对角线互相垂直
2．对角线长为4cm的正方形其边长为（ ）
A．2cmB．cmC．4cmD．cm
3．如图，已知正方形ABCD的边长为5，E为BC边上的一点，∠EBC=30°，则BE的长为 ( )
A．cmB．2cm C．5 cmD．10 cm
4．如图，在菱形中，对角线，相交于点，添加下列条件，能使菱形成为正方形的是（ ）
A．B．C．D．平分
5．如图，延长正方形边至点，使，则为（ ）
A．22.5°B．25°C．30°D．45°
6．下列条件能判定四边形ABCD为正方形的是（ ）
A．四边相等，且对角线互相垂直
B．四角相等，且对角线相等
C．对角线相等且互相垂直平分
D．四边相等，且对角线互相平分
7．已知四边形是平行四边形，再从①，②，③，④四个条件中，选两个作为补充条件后，使得四边形是正方形，现有下列四种选法，其中不正确的是（ ）
A．①②B．②③C．①③D．②④
8．如图，在正方形中，点、分别在，上，且，连接，，则下列结论中不一定正确的是（ ）
A．B．
C．D．
9．如图，正方形ABCD，CEGF，且B．C．E三点共线，M为AG的中点．若AB＝3，CE＝1，则CM的长为（ ）
A．2.5B．C．D．2
10．如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥ CD于点F，连接EF，给出下列五个结论：① AP＝EF；② AP⊥ EF；③∠PFE＝∠BAP；④ PD＝EC；⑤ PB2+PD2＝2PA2，正确结论是（ ）
A．① ③B．① ② ③C．① ③ ⑤D．① ② ③ ⑤
二、填空题
11．正方形ABCD的对角线，则此正方形的面积为____________．
12．如图，在菱形中，对角线与相交于点O，添加一个条件____________，使菱形是正方形．
13．如图，已知正方形ABCD，点E在边DC上，DE=4，EC=2，则AE的长为___ ．
​
14．如图，正方形ABCD中，点E、F分别是BC、AB边上的点，且AE⊥DF，垂足为点O，△AOD的面积为，则图中阴影部分的面积为_____．
15．在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是___________．
16．如图，在正方形中．若以为底边向其形外作等腰直角，连接，则的长为______．
17．如图1，在正方形中，分别为边上的点，HA=EB=FC=GD，连接，交点为．将正方形沿线段剪开，再把得到的四个四边形按图2的方式拼接成一个四边形．若正方形的边长为，，则图2中阴影部分的面积为______．

18．如图，以的斜边为一边，在的右侧作正方形，正方形的对角线交于点O，连接，如果，，那么______．
三、解答题
19．如图，是正方形，是上任意一点，于，于．求证:．
20．如图所示，正方形ABCD的边长为6，点E为BC的中点，点F在AB边上，．求的度数．
21．如图，E，F，M，N分别是正方形四条边上的点，且．试判断四边形是什么图形，并证明你的结论．
22．如图 ，已知点 C 为线段 AB 上一点，四边形ACMF、BCNE 是两个正方形．求证：AN=BM
23．如图，四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE＝BF，连接AE，AF，EF．
(1)求证：△ADE≌△ABF；
(2)若BC＝8，DE＝6，求EF的长．
24．如图，在矩形ABCD中，点E在边AD上，连接CE，以CE为边向右上方作正方形CEFG，作FH⊥AD，垂足为H，连接AF．
（1）求证：FH＝ED；
（2）若AB＝3，AD＝5，当AE＝1时，求∠FAD的度数．
25．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．
(1)的大小＝______°；
(2)求证：≌；
(3)若，则的大小＝______°．
26．如图1，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．
(1)求证：AE=BF；
(2)若AB=8，BG=6，求EF的长；
(3)如图2，连接DF、CE，探究线段DF与CE的数量关系和位置关系并证明．
27．已知正方形ABCD．点E在AB上，点G在AD．点F在射线BC上，点H在CD上．
(1)如图1．，求证：；
(2)如图2，，P为EF中点，求证：；
(3)如图3，EH交FG于O，，若，，则线段EH的长．