数学九年级上册1 菱形的性质与判定示范课ppt课件

这是一份数学九年级上册1 菱形的性质与判定示范课ppt课件，共26页。PPT课件主要包含了学习目标，情境导入，探究新知，菱形的定义，菱形的性质，菱形的四条边都相等，菱形的特殊性质，几何语言，∴AC⊥BD，由垂直想到什么等内容，欢迎下载使用。

1．理解菱形的概念，掌握菱形的性质．2．培养学生主动探究的习惯、严密的思维意识和审美意识．3．经历探索菱形的性质和基本概念的过程，在操作、观察、分析过程中发展学生思维意识，体会几何说理的基本方法．
边：平行四边形的对边平行且相等.
角：平行四边形的对角相等，邻角互补.
对角线：平行四边形的对角线互相平分.
对称性：平行四边形是中心对称图形.
一、回忆一下，什么是平行四边形，它有哪些性质？
二、下面几幅图片中都含有一些平行四边形.观察这些平行四边形，你能发现它们有什么样的共同特征？
通过观察发现这些平行四边形的邻边都相等，这就是本节课要研究的特殊平行四边形——菱形.
菱形的概念及其与平行四边形的关系
观察平行四边形图形的变化，你有什么发现？
有一组邻边相等的平行四边形叫做菱形.
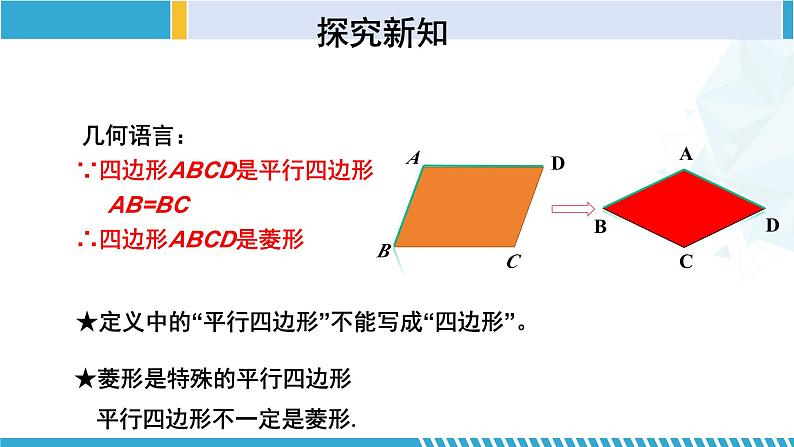
几何语言：∵四边形ABCD是平行四边形 AB=BC∴四边形ABCD是菱形
★菱形是特殊的平行四边形
★定义中的“平行四边形”不能写成“四边形”。
平行四边形不一定是菱形.
（1）菱形是特殊的平行四边形，它具有一般平行四边形的所有性质。你能列举一些这样的性质吗？
菱形的对边平行且相等，对角相等，对角线互相平分。
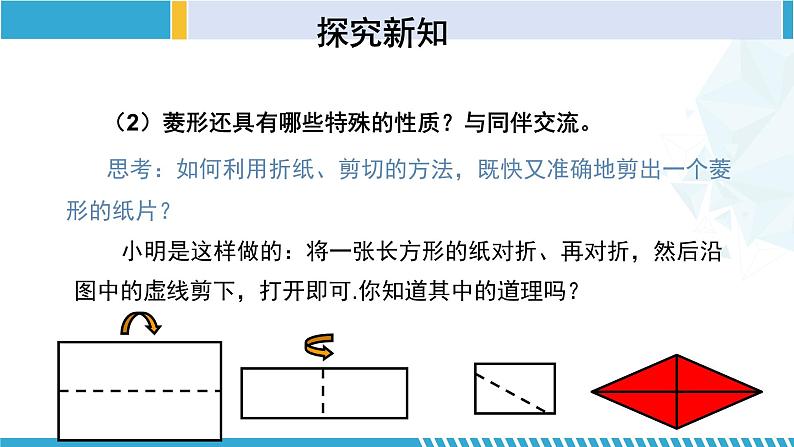
（2）菱形还具有哪些特殊的性质？与同伴交流。
小明是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可.你知道其中的道理吗？
思考：如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？
在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图），并思考以下问题:
1.菱形是轴对称图形吗?如果是,指出它的对称轴.对称轴之间有什么位置关系？是，两条对角线所在直线都是它的对称轴. 两条对称轴互相垂直
2.菱形中有哪些相等的线段？
思考：该结论如何证明呢？
已知：如图，在菱形ABCD中，AB=AD,对角线AC与BD相交于点O.求证明: (1)AB=BC=CD=AD; (2)AC⊥BD.
证明：(1) ∵四边形ABCD是菱形 ∴AB=CD, AD=BC 又∵AB=AD ∴AB=BC=CD=AD
(2)∵AB=AD ∴ △ABD是等腰三角形 又∵四边形ABCD是菱形 ∴OB=OD 在等腰三角形ABD中 ∵OB=OD ∴ AO⊥BD 即AC⊥BD
思考：根据等腰三角形性质，还能推出什么性质？
在等腰三角形ABD中 ∵OB=OD ∴ AO⊥BD ∴ AO平分∠BAD， 即∠DAC=∠BAC. 同理可证∠DCA=∠BCA， ∠ADB=∠CDB，∠ABD=∠CBD.
性质推论：菱形的每一条对角线平分一组对角.
定理一：菱形的四条边都相等
∵四边形ABCD是平行四边形
∴AB=BC=CD=AD
定理二：菱形的对角线互相垂直
类比平行四边形的性质，从边、角、对角线、对称性四方面有条理的将结论进行归纳.
每一条对角线平分一组对角
既是中心对称图形又是轴对称图形
例1 如图，在菱形 ABCD 中，对角线 AC 与 BD相交于点 O, ∠BAD = 60°，BD = 6，求菱形的边长 AB 和对角线 AC 的长。
解：∵四边形 ABCD 是菱形，∴AB=AD（菱形的四条边相等），AC⊥BD（菱形的对角线互相垂直），OB=OD= BD= =3（菱形的对角线互相平分）.
在等腰三角形 ABD 中，∵∠BAD=60°，∴△ABD是等边三角形.∴AB=BD=6.在Rt△AOB中，由勾股定理，得OA2 + OB2 = AB2，∴OA= .∴AC=2OA= （菱形的对角线互相平分）
1．菱形具有而平行四边形不一定具有的性质是( )A．内角和为360° B．对角线互相垂直 C．对边平行 D．对角线互相平行
2．已知菱形的一条对角线与边长相等，则菱形的邻角度数分别为( )A．45°，135° B．60°，120°C．90°，90° D．30°，150°
3.如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节A，E间的距离．若A，E间的距离调节到60 cm，菱形的边长AB＝20 cm，则∠DAB的度数是(　　)。A．90° B．100° C．120° D．150°
4.如图，在菱形ABCD中，P是对角线AC上一动点，过点P作PE⊥BC于点E，PF⊥AB于点F.若菱形ABCD的周长为20，面积为24，则PE＋PF的值为(　　)A. 4B.C. 6D.
5.如图，在菱形ABCD中，E，F分别是AD，BD的中点，若EF＝5，则菱形ABCD的周长为(　　)A．20 B．30 C．40 D．50
6．已知菱形ABCD的周长为8cm，则菱形的边长为____cm.7．已知菱形ABCD的两条对角线AC＝10cm，BD＝24cm，则菱形ABCD的周长为____cm.
8.如图，在菱形ABCD中，对角线AC、BD相交于点O，BD＝12cm，AC＝6cm，求菱形的周长．
解：∵四边形ABCD是菱形，∴AC⊥BD，AO＝ AC，BO＝ BD.∵AC＝6cm，BD＝12cm，∴AO＝3cm，BO＝6cm.在Rt△ABO中，由勾股定理得∴菱形的周长＝4AB＝4×3 ＝12 (cm)．
9.如图，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF. 求证：△ABF≌△DAE；
证明：∵四边形ABCD是菱形，∴AB＝AD，AD∥BC.∴∠BPA＝∠DAE.∵∠ABC＝∠AED，∴∠BAF＝∠ADE.∵∠ABF＝∠BPF，∠BPA＝∠DAE，∴∠ABF＝∠DAE.又∵AB＝DA，∴△ABF≌△DAE(ASA)．
10.如图，在菱形ABCD中，CE⊥AB于点E，CF⊥AD于点F，求证：AE＝AF.
证明：连接AC. ∵四边形ABCD是菱形， ∴AC平分∠BAD， 即∠BAC＝∠DAC. ∵CE⊥AB，CF⊥AD， ∴∠AEC＝∠AFC＝90°. 又∵AC＝AC， ∴△ACE≌△ACF. ∴AE＝AF.
菱形的定义：有一组邻边相等的平行四边形是菱形。
1.对边平行，且四边都相等;
3.对角线互相平分且互相垂直 ．
4.菱形既是中心对称图形,又是轴对称图形