初中数学北师大版七年级下册第一章 整式的乘除4 整式的乘法教学演示课件ppt

这是一份初中数学北师大版七年级下册第一章 整式的乘除4 整式的乘法教学演示课件ppt，共27页。PPT课件主要包含了学习目标，情境导入，①不能漏乘，探究新知，多项式乘多项式，+mb，+an，+ab，归纳总结，多项式与多项式相乘等内容，欢迎下载使用。
　1．理解多项式与多项式相乘的法则，并能运用法则进行计算．　2．理解算理，发展学生的运算能力和几何直观，体会转化、数形结合和程序化思想.
1.如何进行单项式与多项式乘法的运算？
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项；
2.进行单项式与多项式乘法运算时，要注意什么?
即单项式要乘遍多项式的每一项；
② 去括号时注意符号的确定.
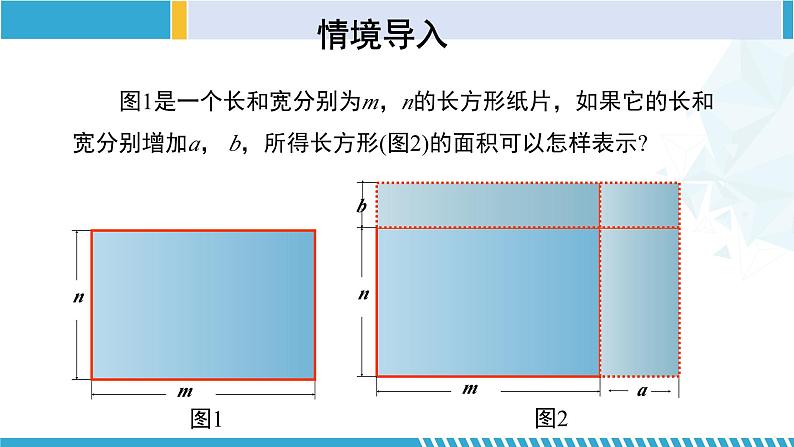
图1是一个长和宽分别为m，n的长方形纸片，如果它的长和宽分别增加a， b，所得长方形(图2)的面积可以怎样表示?
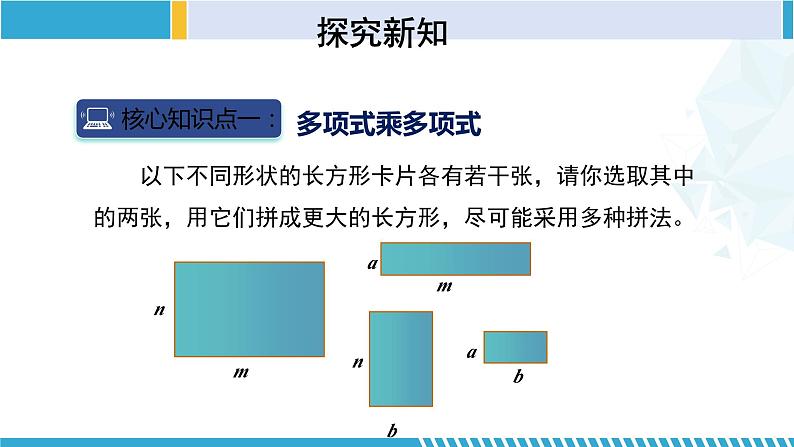
以下不同形状的长方形卡片各有若干张，请你选取其中的两张，用它们拼成更大的长方形，尽可能采用多种拼法。
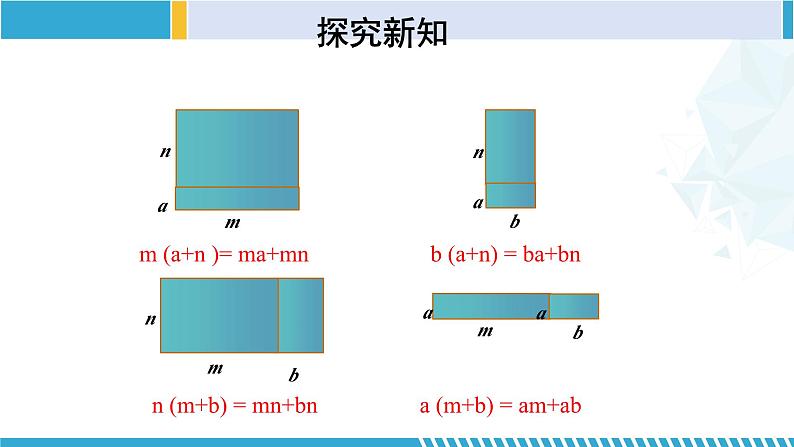
n (m+b) = mn+bn
a (m+b) = am+ab
b (a+n) = ba+bn
m (a+n )= ma+mn
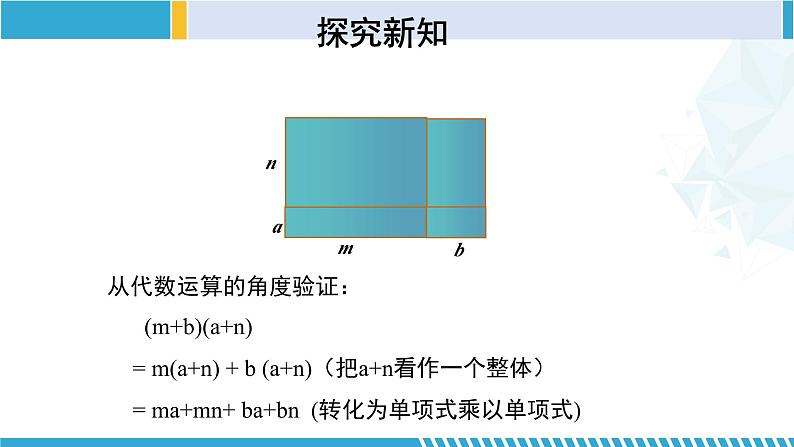
(m+b)(a+n) = m(a+n) + b (a+n)（把a+n看作一个整体） = ma+mn+ ba+bn (转化为单项式乘以单项式)
从代数运算的角度验证：
(m + a )(n + b )＝mn + mb + an + ab .
你能类比单项式与多项式相乘的法则，叙述多项式 与多项式相乘的法则吗？
(m+a) (n + b)
多乘多，来计算，多项式各项都见面，乘后结果要相加，化简、排列才算完.
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
例1 计算：(1) (1－x) (0.6－x)； (2) (2x + y) (x－y) .
解：(1) (1－x) (0.6－x)=1×0.6－1× x + x×0.6 + x·x=0.6－x－0.6x+ x2 =0.6－1.6x+ x2 ；
(2) (2x + y) (x－y) =2x·x－2x·y + y·x－y·y =2x2－2xy+xy－y2=2x2－xy－y2.
多项式乘以多项式时，应注意以下几点：(1)相乘时，按一定的顺序进行，必须做到不重不漏；(2)多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积；(3)相乘后，若有同类项应该合并．
例2：计算:(1)(3x+1)(x+2)； (2)(x-8y)(x-y)； (3) (x+y)(x2-xy+y2).
解： (1) 原式=3x·x+2·3x+1·x+1×2 =3x2+6x+x+2
(2) 原式=x·x-xy-8xy+8y2
=x2-9xy+8y2；
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2 =x3-x2y+xy2+x2y-xy2+y3 = x3+y3.
例3： 先化简，再求值：(a－2b)(a2＋2ab＋4b2)－a(a－5b)(a＋3b)，其中a＝－1，b＝1.
解：原式＝a3－8b3－(a2－5ab)(a＋3b)＝a3－8b3－a3－3a2b＋5a2b＋15ab2＝－8b3＋2a2b＋15ab2.当a＝－1，b＝1时，原式＝－8＋2－15＝－21.
1. 下列计算中，结果为x2＋5x-6的算式是(　　)A. (x＋2)(x＋3) B. (x＋2)(x-3)C. (x＋6)(x-1) D. (x-2)(x-3)2. 若（x-3）（x+4）=x2+px+q，则p，q的值是（　　）A． p=1，q=-12 B． p=-1，q=12C． p=7，q=12 D． p=7，q=-12
3． 如果（x-2）（x-3）=x2+px+q，那么p，q的值是（　　）A． p=-5，q=6 B． p=1，q=-6C． p=1，q=6 D． p=-1，q=64. 若(x+3)(2x-5)=2x2+bx-15 ,则b为(　　)A. -2 B. 2 C. 1 D. -1
5. 下列计算错误的是(　　)A. (1-3x)(1+3x)=1-9x2B. C. -m(x+y)=-mx+myD. (x-y)(a-b)=ax-ay-bx+by6. 如果（x-2）（x+1）=x2+mx+n，那么m+n的值为（　　）A． -1 B． 1 C． -3 D． 3
7． 如图7，有正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，那么需要A类、B类和C类卡片的张数分别为（　　）A． 2，3，7B． 3，7，2C． 2，5，3D． 2，5，7
8. 计算：（1）(x-7)(x+3)-x(x-2)．（2）2x(x-4)+(3x-1)(x+3)．
解：原式=x2-4x-21-x2+2x =-2x-21．　
解：原式=2x2-8x+（3x2+9x-x-3）=2x2-8x+3x2+8x-3=5x2-3．
8.计算：（3）x(x2+x-1)-(2x2-1)(x-4)．
解：原式=x3+x2-x-(2x3-8x2-x+4)=x3+x2-x-2x3+8x2+x-4=-x3+9x2-4.
（4）(x+5)(2x-3)-2x(x2-2x+3).
解：原式=2x2-3x+10x-15-2x3+4x2-6x=-2x3+6x2+x-15.
9. 已知(x3+mx+n)(x2-3x+4)展开式中不含x3和x2项.(1)求m，n的值；(2)当m，n取第(1)小题的值时，求(m+n)(m2-mn+n2)的值.
（2）因为(m+n)(m2-mn+n2)=m3-m2n+mn2+m2n-mn2+n3=m3+n3， 当m=-4，n=-12时，原式=(-4)3+(-12)3=-64-1 728=-1 792.
10. 如图，某校有一块长为（3a+b） m，宽为（2a+b）m的长方形空地，中间是边长为（a+b）m的正方形草坪，其余为活动场地，学校计划将活动场地（阴影部分）进行硬化．（1）用含a，b的代数式表示需要硬化的面积并化简；（2）当a=5，b=2时，求需要硬化的面积．
解：（1）需要硬化的面积表示为(3a+b)(2a+b)-(a+b)2=6a2+3ab+2ab+b2-(a2+2ab+b2)=5a2+3ab.（2）当a=5，b=2时，5a2+3ab=5×25+3×5×2=155（m2）．所以需要硬化的面积为155 m2．
1. 多项式与多项式相乘时要按一定的顺序进行，做 到不重不漏．2. 多项式与多项式相乘时每一项都包含符号，在计 算时先准确地确定积的符号．3. 多项式与多项式相乘的结果若含有同类项，必须 合并同类项．在合并同类项之前的项数应该等于 两个多项式的项数之积．