北师大版八年级下册1 等腰三角形教学ppt课件

这是一份北师大版八年级下册1 等腰三角形教学ppt课件，共29页。PPT课件主要包含了复习导入，探索新知，归纳总结，思维拓展，典例精练，课堂练习，课堂小结，布置作业，谢谢聆听等内容，欢迎下载使用。
定理:等腰三角形的两个底角相等(等边对等角).
数学语言：∵如图，在△ABC中，AB=AC, ∴∠B=∠C (等边对等角)
∵AB=AC, ∠1=∠2 ∴BD=CD,AD⊥BC
∵AB=AC, BD=CD ∴∠1=∠2,AD⊥BC
∵AB=AC, AD⊥BC ∴BD=CD, ∠1=∠2
数学语言：如图,在△ABC中,
推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合（三线合一 ）
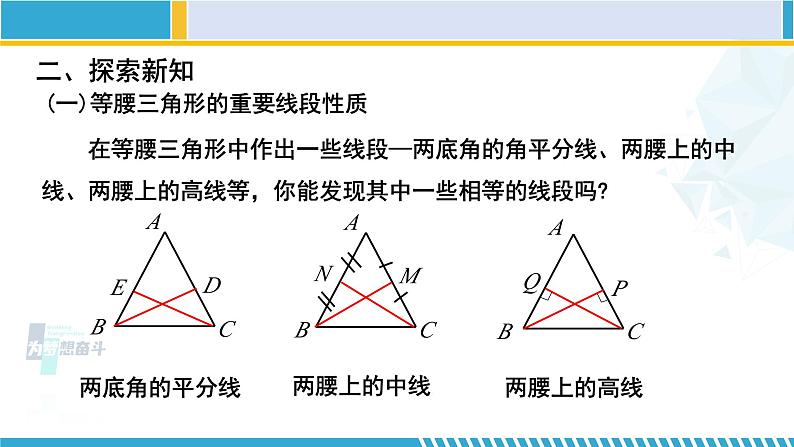
在等腰三角形中作出一些线段—两底角的角平分线、两腰上的中线、两腰上的高线等，你能发现其中一些相等的线段吗?
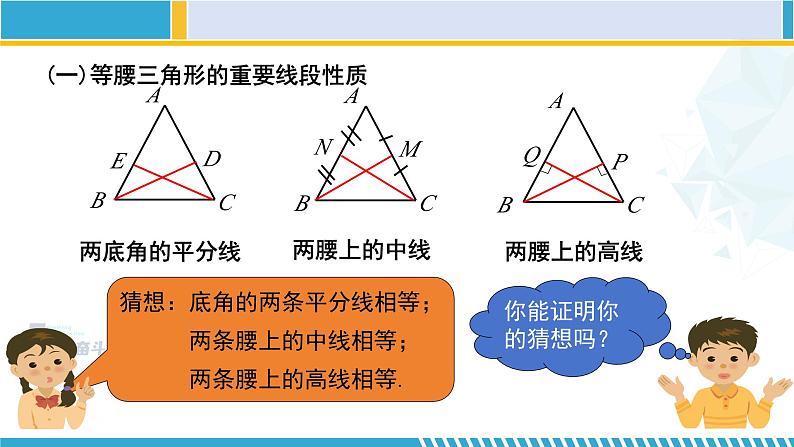
(一)等腰三角形的重要线段性质
猜想：底角的两条平分线相等； 两条腰上的中线相等； 两条腰上的高线相等.
证明: 等腰三角形两底角的平分线相等．
如图, 在△ABC中, AB=AC, BD和CE是△ABC的角平分线．
∠2= ∠ACB,
∵AB=AC，∴∠ABC=∠ACB
∴∠1= ∠ABC，
在△BDC与△CEB中，
∠DCB=∠ EBC（已知），
BC=CB（公共边），
　∠1=∠2（已证），
∴△BDC≌△CEB（ASA）
∴BD=CE(全等三角形的对应边相等)．
∵BD、CE是△ABC的角平分线
∴CM= ，BN=　 ，
证明: 等腰三角形两腰上的中线相等．
已知：如图，在△ABC中，AB=AC，BM,CN是△ABC两腰上的中线．
∵AB=AC，∴∠ABC=∠ACB.
∴CM=BN在△BMC与△CNB中，
∵ BC=CB,∠MCB=∠NBC, CM=BN，
∴△BMC≌△CNB（SAS）．
∵BM,CN是△ABC两腰上的中线
证明: 等腰三角形两腰上的高相等．
已知：如图，在△ABC中，AB=AC，BP,CQ是△ABC两腰上的高．
在△BMC与△CNB中，
∵ BC=CB,∠QBC=∠PCB, ∠BQC=∠CPB，
∴△BQC≌△CPB（AAS）
∵BP,CQ是△ABC两腰上的高∴∠QBC=∠PCB=90°
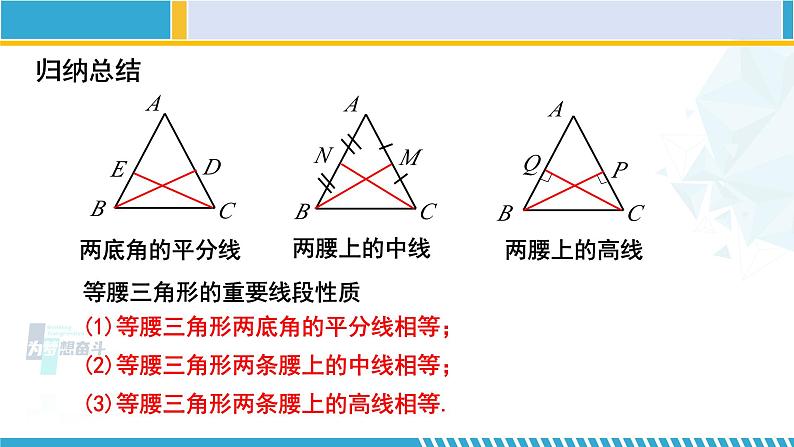
等腰三角形的重要线段性质
(1)等腰三角形两底角的平分线相等；(2)等腰三角形两条腰上的中线相等；(3)等腰三角形两条腰上的高线相等.
1.如图，在△ABC中，AB=AC.（1）如果∠ABD= ∠ABC ， ∠ACE= ∠ACB， 那么BD=CE吗? 为什么？
（2）如果∠ABD= ∠ABC ，∠ACE= ∠ACB 呢?
由此你能得到一个什么结论?
结论：过底边的端点且与底边夹角相等的两线段相等.
△ABD≌△ACE（ASA）
2.如图，在△ABC中，AB=AC.(1)如果AD= AC，AE= AB，那么BD=CE吗?
(2)如果AD= AC，AE= AB呢？
(3)如果AD= AC，AE= AB呢？
结论：两腰上距顶点等距的两点与底边顶点的连线段相等.
这里是一个由特殊结论归纳出一般结论的一种数学思想方法.
(1)过底边的端点且与底边夹角相等的两线段相等.∵在△ABC中，AB=AC，∠ABD=∠ACE， ∴BD=CE.
(2)两腰上距顶点等距的两点与底边顶点的连线段相等∵在△ABC中，AB=AC，AD=AE，∴BD=CE.
等边三角形定义：三边都相等的三角形叫等边三角形；
（二）等边三角形的性质
可以利用等腰三角形的性质进行证明.
定理：等边三角形三个内角都相等，并且每个内角都等于60°.
思考：等边三角形是特殊的等腰三角形，那么等边三角形的内角有什么特征呢？
已知：如图,在△ABC中， AB=AC=BC．求证：∠A=∠B=∠C=60°．
证明：在△ABC中，∵AB=AC(已知)，∴∠B=∠C(等边对等角).同理∠A=∠B．又∵∠A+∠B+∠C=180°(三角形的内角和等于180°)，∴∠A=∠B=∠C=60°．
定理： 等边三角形的三个内角都相等，并且每个角都等于60°
∵如图，在△ABC中， AB=AC=BC．∴∠A=∠B=∠C=60°．
定理： 等边三角形的三个内角都相等，并且每个角都等于60°.
等边三角形的内角性质：
知识点一：等腰三角形的有关线段
例1：如图，在△ABC中，AB＝AC，D是BC的中点，点E、F分别在AB和AC上，且AE=AF，求证：DE＝DF．
在△BED与△CFD中，
∴△BED≌△CFD（SAS）
∵AB=AC，∴∠B=∠C.
∵D是BC的中点，∴BD=CD
BD=CD，∠B=∠C，BE=CF
∵AB=AC，AE=AF，∴BE=CF.
知识点二：等边三角形的性质
例2：如图，在等边三角形ABC中，点M，N分别是等边△ABC的两边AB，AC上的点，且AN＝BM，求证：(1)△BMC≌△ANB； (2)∠MOB＝60°．
证明：（1）∵等边三角形ABC中， ∴AB＝BC，∠A＝∠CBM， ∵在△BMC和△ANB中 AB＝BC，∠A＝∠CBM，AN＝BM， ∴△BMC≌△ANB（SAS）
证明：（2）∵△BMC≌△ANB ∴∠BCM＝∠ABN， ∴ ∠MOB=∠BCM+∠OBC =∠ABN+∠OBC ＝∠ABC=60° ∴∠MOB＝60°
1．已知等腰△ABC中，AB＝AC，那么下列说法中不正确的是（　　）A．BC边上的高和中线互相重合B．AB与AC边上的中线相等C．△ABC中，∠B与∠C的平分线相等D．AB、BC边上的高相等
2．如图，在等腰△ABC中，AB＝AC，BD⊥AC，∠ABC＝72°， 则∠ABD等于( ) A．36° B．54° C．18° D．64°
3．如图，AD，CE分别是△ABC的中线和角平分线．若AB＝AC，∠CAD＝20°，则∠ACE的度数是( ) A．20° B．35° C．40° D．70°
4．如图，△ABC为等边三角形，延长CB到点D，使BD＝BC．延长BC到点E，使CE＝BC．连接AD，AE，则∠DAE的度数是（　　）
A．130°B．120°C．110°D．100°
5．如图，△ABC是等边三角形，P为BC上一点，在AC上取一点D，使AD＝AP，且∠APD＝70°，则∠PAB的度数是（　　）
A．10°B．15°C．20°D．25°
6. 如图，在△ABC中，AB＝AC，D是BC上的一点，DE⊥AB，DF⊥AC，垂足分别为E、F，BE＝CF，求证：DE＝DF．
∴△BED≌△CFD（AAS）．
∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°
∠B=∠C，BE＝CF，∠DEB=∠DFC=90°
7．如图，若△ABC是等边三角形，AB＝6，BD是∠ABC的平分线，延长BC到点E，使CE＝CD，求BE的长度．
解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵BD是∠ABC的平分线，∴AD＝CD＝ AC，∠DBC＝ ∠ABC＝30°，∵CE＝CD，∴CE＝ AC＝3，∴BE＝BC+CE＝6+3＝9．
8．如图，△ABC和△ADE是等边三角形．连接BD、CE，证明：BD＝CE．
证明：∵△ABC和△ADE是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60° ∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC， 即∠BAD＝∠CAE．在△BAD与△CAE中，∵AB＝AC，∠BAD＝∠CAE，AD＝AE ∴△BAD≌△CAE（SAS）．∴BD＝CE（全等三角形的对应边相等）．
小结：通过本节课的学习，谈谈收获及疑惑
等腰三角形重要的线段性质：底角的两条平分线相等；两条腰上的中线相等；两条腰上的高线相等.
完成课本P7习题1.2中第1、2、3、4题
数学中的一些美丽定理具有这样的特性: 它们极易从事实中归纳出来, 但证明却隐藏的极深.——高斯 (Gauss)