北师大版八年级数学上册同步精品课堂 第七章 平行线的证明单元复习（课件）

这是一份北师大版八年级数学上册同步精品课堂 第七章 平行线的证明单元复习（课件），共23页。

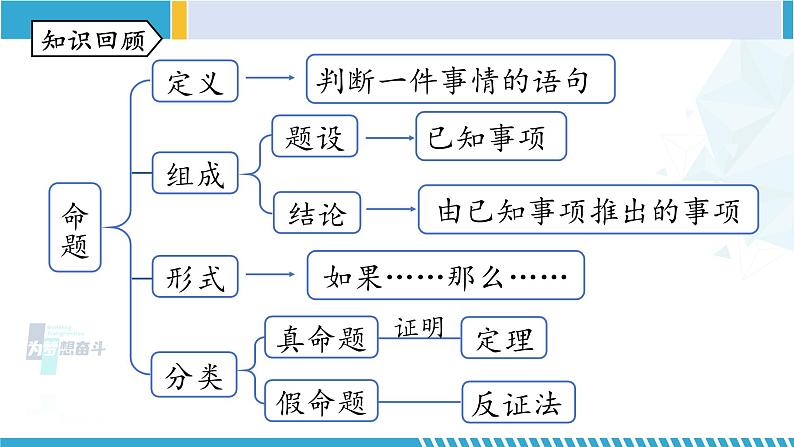
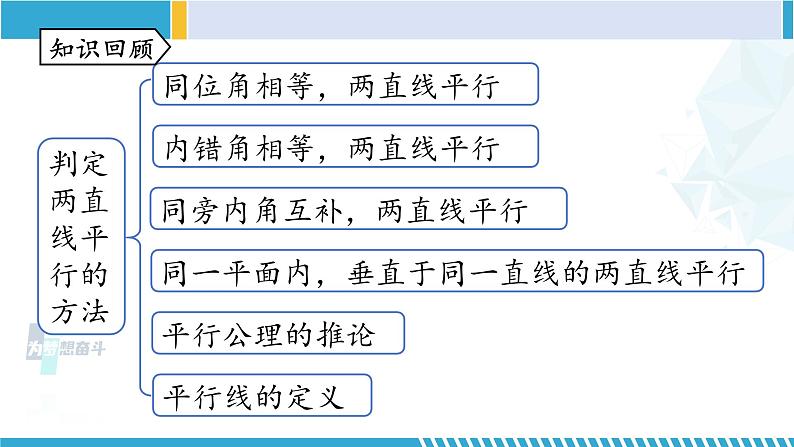
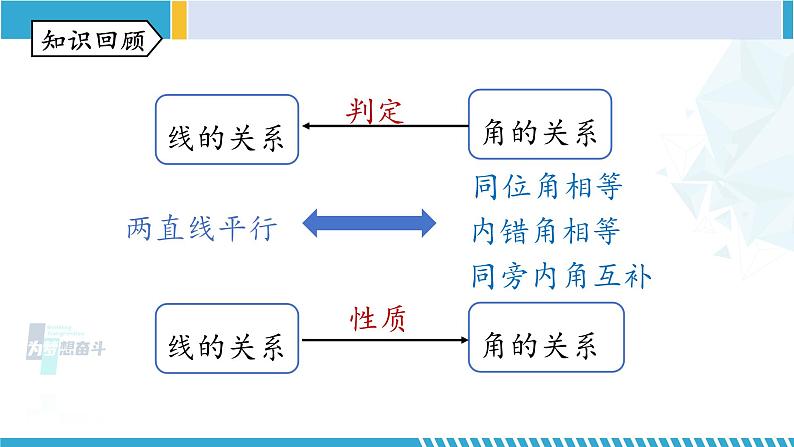
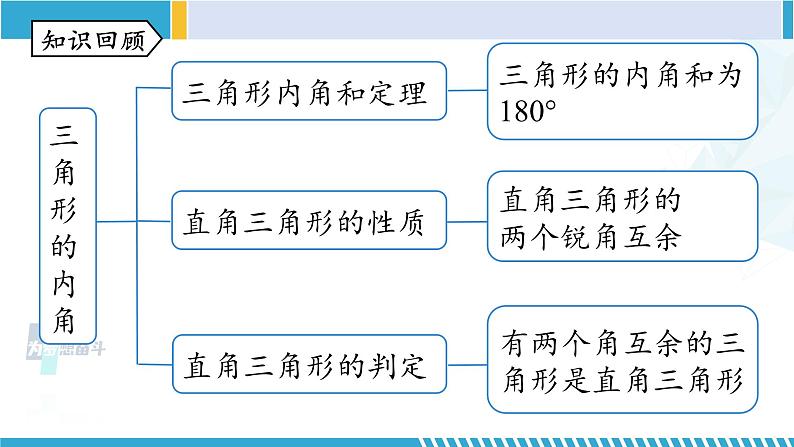
第七章平行线复习课件初中数学知识回顾命题定义组成分类题设结论真命题假命题形式定理证明反证法同位角相等，两直线平行判定两直线平行的方法内错角相等，两直线平行同旁内角互补，两直线平行同一平面内，垂直于同一直线的两直线平行平行线的定义平行公理的推论知识回顾两直线平行 同位角相等内错角相等同旁内角互补线的关系角的关系性质角的关系线的关系判定知识回顾三角形的内角直角三角形的判定有两个角互余的三角形是直角三角形直角三角形的两个锐角互余三角形的内角和为180°知识回顾 A随堂练习 2.下列命题：① 两个锐角之和一定是钝角；② 内错角相等；③ 若 x=y，则 x2=y2；④ 若 x2=y2，则 x =y；⑤ 两点之间，线段最短.其中，真命题有( )A.1个 B.2个 C.3个 D.4个 两直线不平行时不成立 B3. 已知：如图，∠1=∠2，∠3=∠4. 求证：EG∥FH.证明：∵∠1=∠2(已知)，∠AEF=∠1 (对顶角相等)，∴∠AEF=∠2 (等量代换).∴AB∥CD (同位角相等，两直线平行).∴∠BEF=∠CFE (两直线平行，内错角相等). ∵∠3=∠4(已知)，∴∠BEF－∠4=∠CFE－∠3.即∠GEF=∠HFE (等式的性质).∴EG∥FH (内错角相等，两直线平行).4.如图，在下列条件中，能说明 AC//DE 的是( )A.∠A =∠CFDB.∠BED =∠EDFC.∠BED =∠AD.∠A+∠AFD =180°AB//DFAB//DFAB//DFCAC//DE5.如图所示，一条公路修到湖边时，需要拐弯绕湖而过，第一次拐的角∠A=110°，第二次拐的角∠B=145°，则第三次拐的角∠C = 时，道路 CE 才能恰好与 AD 平行.解析：当第三次拐的角∠C = 145°时，道路 CE 才能恰好与 AD 平行.理由如下：如图，过点 B 作∠ABF = 110°.∵ ∠A =∠ABF =110°，∴ AD//BF(内错角相等，两直线平行).∵ ∠ABC =145°，∠ABF =110°，∴ ∠FBC =∠ABC -∠ABF =35°.F∵ ∠C +∠FBC =145°+35°=180°，∴ BF//CE(同旁内角互补，两直线平行)，∴ CE//AD(平行公理的推论).F解： ∵ AB//CF，∠ABC =70°，∴ ∠BCF=∠ABC= 70°.∵ DE//CF，∴ ∠DCF+∠CDE =180°. 又∠CDE =130°，∴ ∠DCF =50°，∴ ∠BCD =∠BCF -∠DCF =70°- 50° =20°.6.如图，已知 AB//DE//CF，若∠ABC= 70°，∠CDE= 130°，则∠BCD = .20°7.如图，MN，EF 表示两面互相平行的镜面，光线 AB 照射到镜面 MN 上，反射光线为 BC，此时∠1=∠2；光线 BC 经过镜面 EF 反射后的光线为 CD，此时∠3=∠4.试判断 AB 与 CD 的位置关系，并说明理由.判断两直线的位置关系，一般考虑平行或垂直，观察图形猜想AB∥CD.解：AB//CD.理由如下：∵ MN//EF(已知)， ∴ ∠2=∠3(两直线平行，内错角相等).∵ ∠1=∠2，∠3=∠4(已知)，∴ ∠1=∠2=∠3=∠4， ∴∠1+∠2=∠3+∠4.∵ ∠ABC+∠1+∠2=180°， ∠BCD+∠3+∠4=180°(平角的性质)，∴ ∠ABC=∠BCD(等量代换).∴ AB//CD(内错角相等，两直线平行).∠P+∠A+∠C=360°∠P=∠A+∠C8.如图，AB//CD，分别探究下面四个图中∠P 与∠A，∠C之间的关系.EE解：∠APC+∠A=∠C.理由如下：过点 P 作 PE//AB，则∠EPA+∠A=180°.∵ ∠EPA=∠APC+∠1，∴ ∠APC+∠1+∠A=180°，∴ ∠APC+∠A=180°-∠1.∵ AB//CD，∴ PE//CD， ∴ ∠1+∠C=180°，∴ ∠C= 180°-∠1.∴ ∠APC+∠A=∠C.E1解：∠A=∠APC+∠C.理由如下：过点 P 作 PE//AB，则∠1+∠A=180°.∵ AB//CD，∴ PE//CD， ∴ ∠EPC+∠C=180°，即∠1+∠APC+∠C=180°，∴ 180°-∠A+∠APC+∠C=180°.∴ ∠A=∠APC+ ∠C.E19.如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE//BC交AC于点E，若∠A=54°，∠B=48°，则∠CDE的大小是（ ） A.44° B.40° C.39° D.38°E解析：∵∠A=54°，∠B=48°，∴∠ACB=180°-54°-48°=78°.∵CD平分∠ACB， ∴∠DCB=39°. ∵DE//BC，∴∠CDE=∠DCB=39°. C10.如图，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数.分析：利用三角形内角和定理，将已知的角度与未知角之间联系起来.利用等量代换将相等的角进行替换.10.如图，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数.解：∵∠3+∠ADB=180°，∠1+∠2+∠ADB=180°，∴∠3=∠1+∠2.∵∠3=∠4，∠1=∠2， ∴∠4=∠1+∠2=2∠1.∵∠1+∠2+∠4+∠DAC=180°，10.如图，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数.∴∠DAC=180°-∠1-∠2-∠4=180°-4∠1.∵∠BAC=∠1+∠DAC=∠1+（180°-4∠1）=180°-3∠1=63°，∴∠1=39°，∴∠DAC=24°.