数学八年级上册4 一次函数的应用示范课ppt课件

这是一份数学八年级上册4 一次函数的应用示范课ppt课件，共19页。PPT课件主要包含了学习目标，情境导入，vms，例题解析，探索交流，练习巩固，小结反思等内容，欢迎下载使用。

1.了解两个条件可以确定一个一次函数，一个条件可以确定一个正比例函数，并能由此求出表达式.
2.会用待定系数法解决简单的实际问题.
3.能根据函数的图象确定一次函数的表达式.
前面，我们学习了一次函数及其图象和性质，你能写出两个具体的一次函数解析式吗？如何画出它们的图象？
思考：反过来，已知一个一次函数的图象经过两个具体的点，你能求出它的解析式吗？
两点法——两点确定一条直线
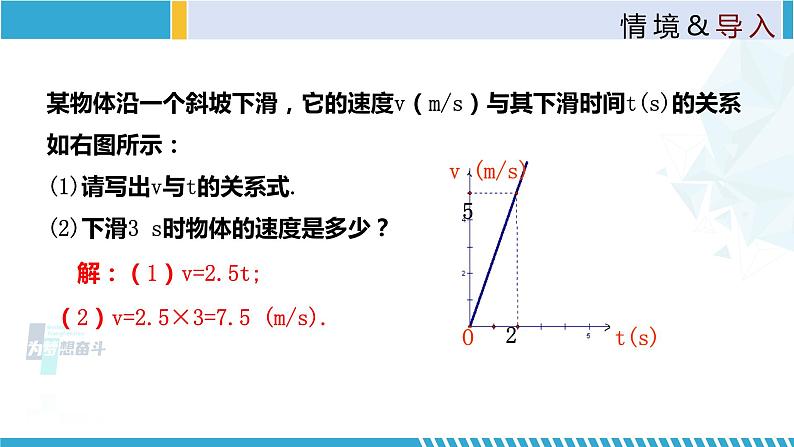
某物体沿一个斜坡下滑，它的速度v（m/s）与其下滑时间t(s)的关系如右图所示： (1)请写出v与t的关系式.(2)下滑3 s时物体的速度是多少？
解：（1）v=2.5t;
（2）v=2.5×3=7.5 (m/s).
例1.已知y与2x成正比例，且当x＝3时，y＝12，求y与x的函数表达式．解：设y＝k·2x(k≠0)．因为当x＝3时，y＝12， 所以12＝2×3×k.所以k＝2. 所以所求的函数表达式为y＝4x.
确定正比例函数的表达式需要几个条件？ 确定一次函数的表达式呢？
例2.在弹性限度内，弹簧的长度 y（cm）是所挂物体质量 x（kg）的一次函数，某弹簧不挂物体时长14.5cm，当所挂物体的质量为3kg时，弹簧长16cm。写出y与x之间的关系式，并求所挂物体的质量为4kg时弹簧的长度。
解：设 y=kx+b，根据题意，得14.5=b ① 16=3k+b ②将①代入②，得 k=0.5所以在弹性限度内，y=0.5x+14.5当 x=4时，y=0.5×4+14.5=16.5（cm）即物体的质量为4kg时，弹簧长度为16.5cm。
例3.已知一次函数的图象经过(0，5)、(2，－5)两点，求一次函数的表达式．
解：设一次函数的表达式为y＝kx＋b，根据题意得，∴－5＝2k＋b，5＝b，解得b＝5，k＝－5.∴一次函数的表达式为y＝－5x＋5.
例4.正比例函数与一次函数的图象如图所示，它们的交点为A(4，3)，B为一次函数的图象与y轴的交点，且OA＝2OB.求正比例函数与一次函数的表达式．
解：设正比例函数的表达式为y1＝k1x，一次函数的表达式为y2＝k2x＋b.∵点A(4，3)是它们的交点，∴代入上述表达式中，得3＝4k1，3＝4k2＋b.∴k1＝ ，即正比例函数的表达式为y＝ x.
∵OA＝ ＝5，且OA＝2OB，∴OB＝ .∵点B在y轴的负半轴上，∴B点的坐标为(0，－ )．又∵点B在一次函数y2＝k2x＋b的图象上，∴－ ＝b，代入3＝4k2＋b中，得k2＝ .∴一次函数的表达式为y2＝ x－ .
总结：求一次函数的表达式都要经过设、列、解、还原四步，设都相同，就是设出一次函数的表达式，列就是把已知两点的坐标代入所设表达式，列出两个一次方程， 解这两个方程，将所求得的系数的值代回所设表达式 即可.
例5.一个一次函数的图象平行于直线y＝－2x，且过点A(－4，2)，求这个函数的表达式．解：∵一次函数图象与直线y=-2x平行，∴设y=-2x+b，把点A（-4,2）代入上式得，2=-2×（-4）+b,∴b=-6.∴这个函数的表达式为y=-2x-6.
1.两条直线平行的规律：两条直线平行 k值相等2.平移规律：“上加下减”，上、下是形的平移，加、减是数的 变化：直线y＝kx＋b可以看作由直线 y＝kx平移得到：①当b＞0时，把直线y＝kx向上平移b个单位得到直线y＝kx＋b；②当b＜0时，把直线y＝kx向下平移|b|个单位得到直线y＝kx＋b.
1.一次函数y=kx+b(k≠0)的图象如图，则下列结论正确的是 ( ) A．k=2　　　B．k=3　　　C．b=2　　D．b=3
2.若一次函数y=3x-b的图象经过点P(1，－1)，则该函数图象必经过点（ ）A.（－1，1） B.(2，2） C.（－2，2） D (2，一2)
3.已知一次函数的图象过点（0，2），且与两坐标轴围成的三角形的面积为2，求此一次函数的表达式.
确定一次函数的关系式，就是确定一次函数关系式y=kx+b(k≠0)中常数k,b的值.2.求一次函数关系式的步骤为：设→代→求→还原，即：(1)设：设出一次函数关系式y=kx+b；(2)代：将所给数据代入函数关系式；(3)求：求出k的值；(4)还原：写出一次函数关系式.