备战2024年高考数学二轮复习专题03解三角形中的组合图形问题(原卷版+解析)

这是一份备战2024年高考数学二轮复习专题03解三角形中的组合图形问题(原卷版+解析)，共31页。试卷主要包含了组合图形中的基本量计算，组合图形中的面积最值问题等内容，欢迎下载使用。
常见考点
考点一 组合图形中的基本量计算
典例1．如图，在平面四边形中，.
（1）求；
（2）若的面积为，求.
变式1-1．如图，在△中，，，，D是线段BC上的点，且.
（1）求线段AD的长度；
（2）求的值.
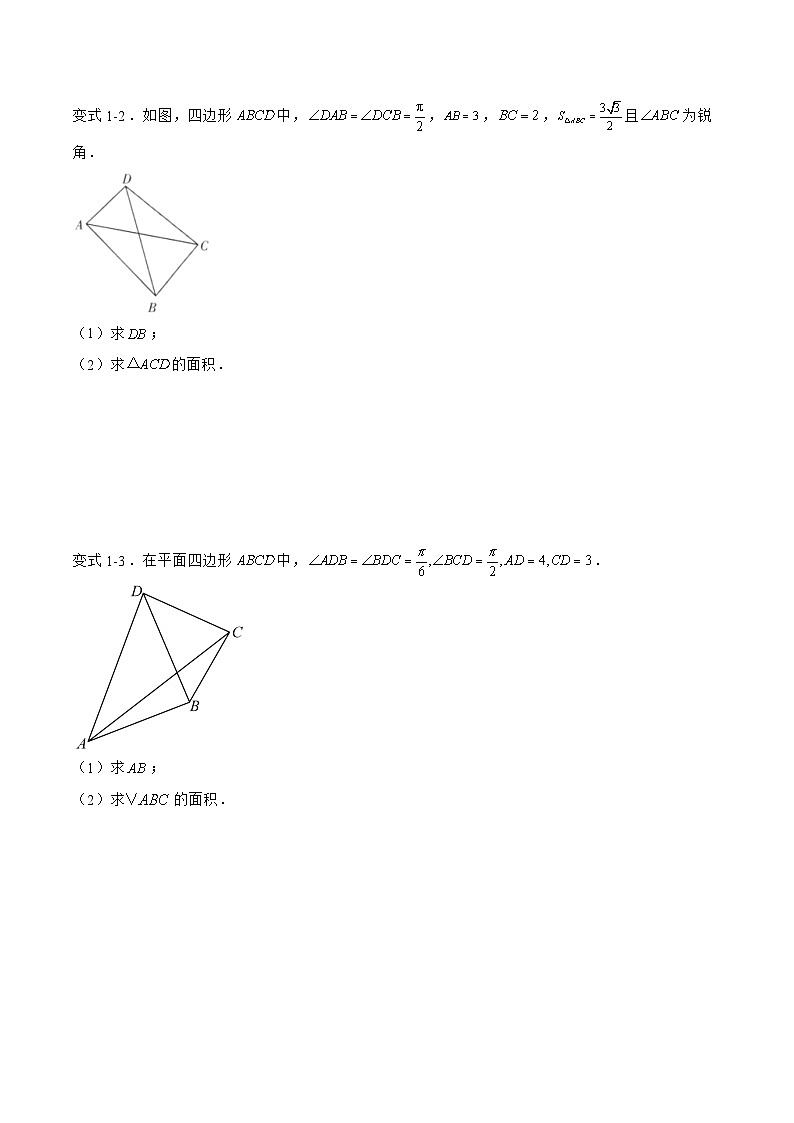
变式1-2．如图，四边形中，，，，且为锐角．
（1）求；
（2）求的面积．
变式1-3．在平面四边形中，．
（1）求；
（2）求的面积．
考点二 组合图形中的面积最值问题
典例2．如图，已知，点是以为圆心，5为半径的半圆上一动点.
（1）当时，求线段的值；
（2）若为正三角形，求四边形面积的最大值.
变式2-1．在中，角A，B，C的对边分别是a，b，c，且满足．
（1）求角A；
（2）如图，若，点D是外一点，，设，求平面四边形面积的最大值及相应的值．
变式2-2．如图，在直角三角形中，，分别在线段上，且为的中点，，设．
（1）求 (用表示)；
（2）求三角形面积的最小值．
变式2-3．为响应国家“乡村振兴”号召，农民老王拟将自家一块直角三角形地按如图规划成3个功能区：区域为荔枝林和放养走地鸡，区域规划为“民宿”供游客住宿及餐饮，区域规划为小型鱼塘养鱼供休闲垂钓．为安全起见，在鱼塘周围筑起护栏．已知，，，．
（1）若，求护栏的长度（的周长）；
（2）若鱼塘的面积是“民宿”的面积的倍，求；
（3）当为何值时，鱼塘的面积最小，最小面积是多少？
巩固练习
练习一 组合图形中的基本量计算
1．如图，在中，，，点在线段上．
（1）若，求的长；
（2）若，的面积为，求的值．
2．如图，在中，，，点D在线段BC上.
（1）若，求AD的长；
（2）若，的面积为，求的值.
3．如图所示，在圆内接四边形ABCD中，M为对角线AC的中点，，，，．
（1）求AB；
（2）求．
4．如图，在中，角所对的边分别为，已知，点为边上的点，且.
（1）求的面积.
（2）求线段的长.
练习二 组合图形中的面积最值问题
5．如图，在中，，，延长至，使得.
（1）若，求的面积；
（2）求面积的取值范围.
6．已知在中，内角A，，的对边分别为，，，满足.
（1）求；
（2）如图，若，在外取点.且，.求四边形面积的最大值.
7．在中，角，，的对边分别是，，，已知.
（1）求角；
（2）若是等腰三角形，且，为的中点，，分别在线段，上（不包含端点），且，设，求面积的最小值.
8．如图，在中，角A，B，C所对的边为a，b，c，．
（1）若，求的长；
（2）若，求面积的最大值．
第一篇 解三角形
专题03 解三角形中的组合图形问题
常见考点
考点一 组合图形中的基本量计算
典例1．如图，在平面四边形中，.
（1）求；
（2）若的面积为，求.
【答案】
（1）
（2）7
【分析】
（1）在中，利用平方关系求出，再根据即可得出答案；
（2）在中，利用正弦定理求得，再根据三角形得面积求得，再利用余弦定理即可得出答案.
（1）
解：在中，
因为，所以，
则；
（2）
解：由（1）得，
又，所以，
在中，因为，
所以，
因为，
所以，
在中，
，
所以.
变式1-1．如图，在△中，，，，D是线段BC上的点，且.
（1）求线段AD的长度；
（2）求的值.
【答案】
（1）；
（2）.
【分析】
（1）法一：向量的加法可得，再应用向量的运算律求的模即可；法二：由余弦定理可得，进而可得，最后根据余弦定理求AD的长度；
（2）法一：由正弦定理的边角关系可得，即可求值；法二：由三角形面积公式有，即可求目标式的值.
（1）
方法一：向量法
∵，
∴，
∴，则.
方法二：根据余弦定理可得：，则，
∴，且，
∴，则.
（2）
方法一：根据正弦定理可得：，，
∴.
方法二：根据三角形面积公式得，，
∴.
变式1-2．如图，四边形中，，，，且为锐角．
（1）求；
（2）求的面积．
【答案】
（1）
（2）
【分析】
（1）由三角形面积公式求得，利用余弦定理求得，分析可知BD是四边形外接圆的直径，再利用正弦定理可求解；
（2）由面积公式即可得解.
（1）
由已知，
∵是锐角，∴．
由余弦定理可得，则．
∵，∴BD是四边形外接圆的直径，
∴BD是外接圆的直径，利用正弦定理知
（2）
由，，，，
则,,
又，则，
因此，
故的面积为．
变式1-3．在平面四边形中，．
（1）求；
（2）求的面积．
【答案】
（1）；
（2）.
【分析】
（1）在中求出，然后在中，利用余弦定理即可求出的长；
（2）首先判断出为直角三角形，从而可求出，然后利用三角形的面积公式即可求出答案.
（1）
因为为直角三角形，，
所以．
在中，，
由余弦定理，得，所以．
（2）
由（1）知，，，所以，
所以为直角三角形，且，
所以，
故．
考点二 组合图形中的面积最值问题
典例2．如图，已知，点是以为圆心，5为半径的半圆上一动点.
（1）当时，求线段的值；
（2）若为正三角形，求四边形面积的最大值.
【答案】
（1）
（2）
【分析】
（1）根据条件利用余弦定理可得答案；
（2）设，用表示出四边形的面积，结合三角函数知识化简求解最值.
（1）
在中，由余弦定理得：
.
所以.
（2）
设，所以，
则
.
所以当时，四边形的面积取得最大值.
变式2-1．在中，角A，B，C的对边分别是a，b，c，且满足．
（1）求角A；
（2）如图，若，点D是外一点，，设，求平面四边形面积的最大值及相应的值．
【答案】
（1）
（2）最大值为，此时
【分析】
（1）利用正弦定理、余弦定理化简已知条件，求得进而求得.
（2）求得平面四边形面积的表达式，结合三角函数最值的求法求得平面四边形面积的最大值及相应的值.
（1）
∵，
由正弦定理知，，
由余弦定理知，.
（2）
由（1）以及，得是等边三角形．
设，则．
余弦定理可得：，
则．
故四边形面积．
∵，∴，
∴当时，S取得最大值为，
故平面四边形面积的最大值为，此时．
变式2-2．如图，在直角三角形中，，分别在线段上，且为的中点，，设．
（1）求 (用表示)；
（2）求三角形面积的最小值．
【答案】
（1）
（2）
【分析】
（1）根据题意得，，进而根据计算即可；
（2）结合题意得，，再结合三角形面积公式和辅助角公式得，再结合三角函数的性质求解即可.
（1）
解：在直角三角形中，，
所以， ；
因为，所以，
即；
在中，因为
（2）
在直角三角形中，因为，所以；
在中，因为，
所以由正弦定理得，，即；
在直角三角形中，
，其中，且；
又因为在线段上，所以，且；
故当时， ．
变式2-3．为响应国家“乡村振兴”号召，农民老王拟将自家一块直角三角形地按如图规划成3个功能区：区域为荔枝林和放养走地鸡，区域规划为“民宿”供游客住宿及餐饮，区域规划为小型鱼塘养鱼供休闲垂钓．为安全起见，在鱼塘周围筑起护栏．已知，，，．
（1）若，求护栏的长度（的周长）；
（2）若鱼塘的面积是“民宿”的面积的倍，求；
（3）当为何值时，鱼塘的面积最小，最小面积是多少？
【答案】
（1）
（2）
（3）时，的面积取最小值为
【分析】
（1）先根据题干条件得到，，利用余弦定理求出，用勾股定理逆定理得到，进而求出CN，MN，求出护栏的长度；（2）设，利用和的面积关系和正弦定理得到CN的两种表达，列出方程，求出；（3）结合第二问的求解，利用正弦定理和面积公式得到面积关于的关系式，求出最小值.
（1）
∵，，，∴，∴，∴，∴，
在中，由余弦定理可得：
，则，∴，∴，∵，∴，∴，∴护栏的长度（的周长）为；
（2）
设（），因为鱼塘的面积是“民宿”的面积的倍，所以，即，，中，由三角形外角定理可得，在中，由，得，从而，即，
由，得，所以，即；
（3）
设（），由（2）知，，
中，由外角定理可得，又在中，由，得，所以
，所以当且仅当，
即时，的面积取最小值为.
巩固练习
练习一 组合图形中的基本量计算
1．如图，在中，，，点在线段上．
（1）若，求的长；
（2）若，的面积为，求的值．
【答案】
（1）；
（2）.
【分析】
（1）利用正弦定理结合两角和的正弦公式化简可得出，利用同角三角函数的平方关系可求得的值，然后在中，利用正弦定理可求得边的长；
（2）设，则，利用三角形的面积公式可求得的值，然后在、中利用正弦定理，再结合，可求得结果.
（1）
解：因为，
由正弦定理可得，
，则，故，则为锐角，所以，，
，则，
在中，由正弦定理得，，解得．
（2）
解：设，则，，则，
即，可得，故，
由余弦定理可得，
在中，由正弦定理可得，故，
在中，由正弦定理可得，故，
因为，
所以，.
2．如图，在中，，，点D在线段BC上.
（1）若，求AD的长；
（2）若，的面积为，求的值.
【答案】
（1）；
（2）.
【分析】
（1）在中，由正弦定理求得；
（2）由题可得面积，由面积公式求得，再由余弦定理求得，然后利用正弦定理即得．
（1）
在三角形中，∵，
∴，
在中，由正弦定理得，
又，，，
∴.
（2）
∵，
∴，，
又的面积为，
∴，
∵，
∴，
∴，
在中，由余弦定理得，
∴，
在中，由正弦定理得
∴.
3．如图所示，在圆内接四边形ABCD中，M为对角线AC的中点，，，，．
（1）求AB；
（2）求．
【答案】
（1）
（2）
【分析】
（1）由，两边平方，解方程得出AB；
（2）由余弦定理得出，再由圆内接四边形的性质以及正弦定理得出．
（1）
根据题意，，
两边平方得，即，
解得或（舍去），即．
（2）
由余弦定理可得，所以，
由题意知，所以，所以．
根据正弦定理得，
因此
4．如图，在中，角所对的边分别为，已知，点为边上的点，且.
（1）求的面积.
（2）求线段的长.
【答案】
（1）
（2）
【分析】
（1）、方法一:求出，根据正弦定理可求出,进而求出,进而求出的面积;
方法二:求出，根据余弦定理可求出,进而求出的面积.
（2）、方法一: 求出，在中根据余弦定理可求出;
方法二:在中由余弦定理可得,在中由余弦定理可得.
（1）
方法一:在中，为锐角，
由正弦定理可得，，，
又为锐角，，
，
方法二：在中，为锐角，，
由余弦定理可得，.，，
，或（舍去），
，
（2）
方法一：在中，，
在中，由余弦定理得，
,
方法二：在中由余弦定理可得:，
，
在中由余弦定理可得，
,.
练习二 组合图形中的面积最值问题
5．如图，在中，，，延长至，使得.
（1）若，求的面积；
（2）求面积的取值范围.
【答案】
（1）
（2）
【分析】
（1）在中，由正弦定理得，进而在中，根据可得解；
（2）在中，设，则，，在中，由正弦定理得，由，利用恒等变换结合角的范围即可得解.
（1）
在中，，，.由正弦定理知，所以.
因为为锐角，所以，所以.
在中，，，则，
故.
（2）
在中，设，则，.
在中，由正弦定理，得，
所以
由，得，又为锐角，
所以，，所以，
故面积的取值范围是.
6．已知在中，内角A，，的对边分别为，，，满足.
（1）求；
（2）如图，若，在外取点.且，.求四边形面积的最大值.
【答案】
（1）；
（2）.
【分析】
(1)由正弦定理将中的边化为角，再结合正弦的两角和公式化简可求得，从而得解；
(2)易知为等边三角形，在中，由余弦定理可求得，再根据和，可推出四边形的面积，最后由和正弦函数的图象与性质即可得解．
（1）
，
由正弦定理得，，
即，
，，
，．
（2）
因为，，∴△ABC是等边三角形，
在中，由余弦定理知，
，
而，
，
四边形的面积，
，，，
当即时，取得最大值，为，
故四边形面积的最大值为．
7．在中，角，，的对边分别是，，，已知.
（1）求角；
（2）若是等腰三角形，且，为的中点，，分别在线段，上（不包含端点），且，设，求面积的最小值.
【答案】
（1）
（2）
【分析】
（1）根据正弦定理边化角公式及三角函数恒等变换求解即可.
（2）首先利用正弦定理得到，，从而得到，再求其最小值即可.
（1）
因为，所以，
所以，
因为，，所以.
又因为，所以，即.
（2）
因为是等腰三角形，且，为的中点，
所以，，
在中，，所以.
在中，，所以.
因为，所以当时，
取得最小值，.
8．如图，在中，角A，B，C所对的边为a，b，c，．
（1）若，求的长；
（2）若，求面积的最大值．
【答案】
（1）
（2）
【分析】
（1）设，在中分别利用余弦定理可得关于的方程组，从而可求的长；
（2）在中利用余弦定理和基本不等式可求的最大值，从而可求面积的最大值．
（1）
由题意知：，
设，
在中，，所以（1），
而，所以（2）
由（1）（2）得：，解得，所以．
（2）
由（1）知，而为三角形内角，
所以，
因为，所以．
在中，，
所以，当且仅当时时取等号，
所以，
所以面积的最大值为．