
所属成套资源:备战2024年高考数学二轮复习
备战2024年高考数学二轮复习专题04立体几何中的由夹角求其它量问题(原卷版+解析)
展开
这是一份备战2024年高考数学二轮复习专题04立体几何中的由夹角求其它量问题(原卷版+解析),共64页。试卷主要包含了已知线线角求其他量,已知线面角求其他量,已知二面角求其他量等内容,欢迎下载使用。
常见考点
考点一 已知线线角求其他量
典例1.如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AB⊥A1C;
(2)在棱AA1上是否存在一点F,使得异面直线AC1与BF所成角为60°,若存在,求出AF长;若不存在,请说明理由.
变式1-1.如图:在三棱锥中,底面,,点,,分别为棱,,的中点,是线段的中点,,.
(1)求证:平面;
(2)已知点在棱上,且直线与直线所成角的余弦值为,求线段的长.
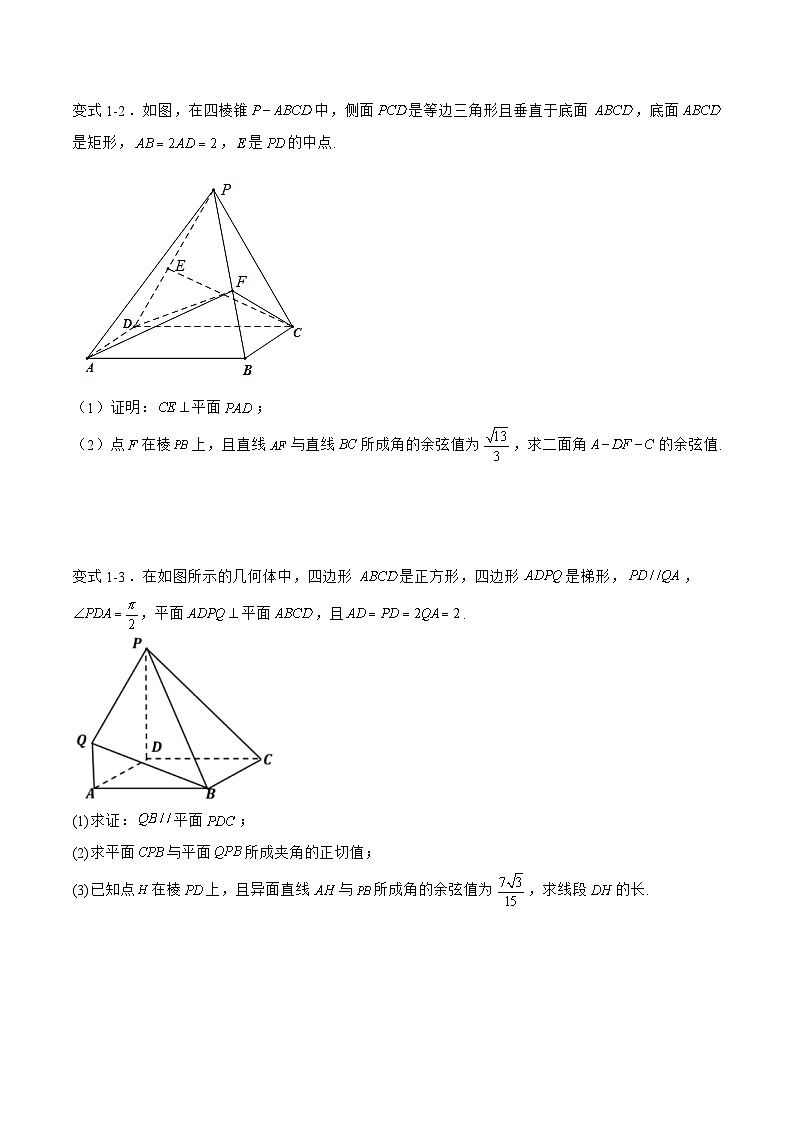
变式1-2.如图,在四棱锥中,侧面是等边三角形且垂直于底面,底面是矩形,,是的中点.
(1)证明:平面;
(2)点在棱上,且直线与直线所成角的余弦值为,求二面角的余弦值.
变式1-3.在如图所示的几何体中,四边形是正方形,四边形是梯形,,,平面平面,且.
(1)求证:平面;
(2)求平面与平面所成夹角的正切值;
(3)已知点在棱上,且异面直线与所成角的余弦值为,求线段的长.
考点二 已知线面角求其他量
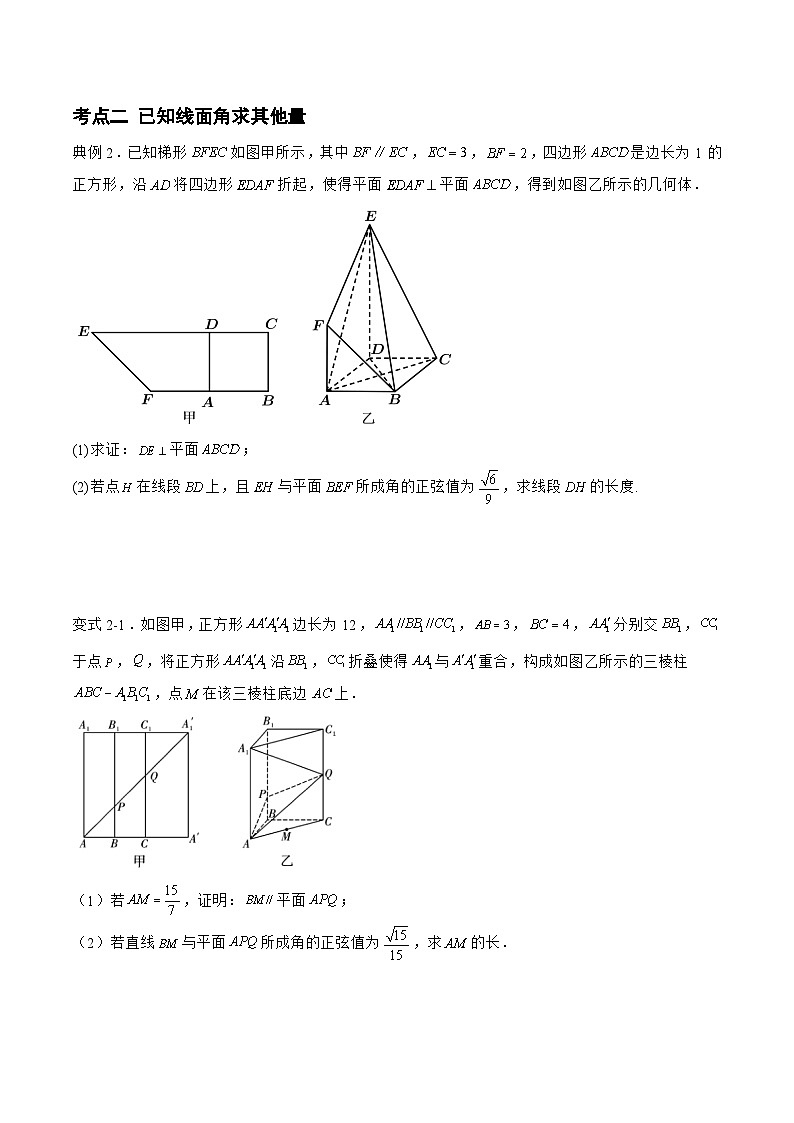
典例2.已知梯形如图甲所示,其中,,,四边形是边长为1的正方形,沿将四边形折起,使得平面平面,得到如图乙所示的几何体.
(1)求证:平面;
(2)若点在线段上,且与平面所成角的正弦值为,求线段的长度.
变式2-1.如图甲,正方形边长为12,,,,分别交,于点,,将正方形沿,折叠使得与重合,构成如图乙所示的三棱柱,点在该三棱柱底边上.
(1)若,证明:平面;
(2)若直线与平面所成角的正弦值为,求的长.
变式2-2.如图,三棱柱所有的棱长为2,,M是棱BC的中点.
(Ⅰ)求证:平面ABC;
(Ⅱ)在线段B1C是否存在一点P,使直线BP与平面A1BC 所成角的正弦值为? 若存在,求出CP的值; 若不存在,请说明理由.
变式2-3.如图所示,四棱锥中,菱形所在的平面,,点、分别是、的中点,是线段上的点.
(1)求证:平面平面;
(2)当时,是否存在点,使直线与平面所成角的正弦值为?若存在,请求出的值,若不存在,请说明理由.
考点三 已知二面角求其他量
典例3.如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
变式3-1.如图1,平面图形PABCD由直角梯形ABCD和拼接而成,其中,、,,,PC与AD相交于O,现沿着AD折成四棱锥(如图2).
(1)当四棱锥的体积最大时,求点B到平面PCD的距离;
(2)在(1)的条件下,线段PD上是否存在一点Q,使得二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.
变式3-2.如图,在三棱锥中,平面ABC,,,于点D,点E在侧棱PC上,且.
(1)证明:平面ACD;
(2)是否存在λ,使二面角的余弦值为?若存在,求出λ的值;若不存在,说明理由.
变式3-3.如图,四棱柱ABCD—A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
(1)求证:平面CC1D1D⊥底面ABCD;
(2)若平面BCC1B1与平面BED1所成的锐二面角的大小为,求线段ED1的长度.
巩固练习
练习一 已知线线角求其他量
1.已知正方形和矩形所在的平面互相垂直,且,,点是线段中点.
(1)求证:平面;
(2)求平面和平面的锐二面角的余弦值;
(3)线段上是否存在点,使得与所成的角为?若存在,请求出的长,若不存在,请说明理由.
2.如图,在三棱锥中,底面.点D,E,N分别为棱的中点,M是线段的中点,,.
(Ⅰ)求证:平面;
(Ⅱ)求二面角的正弦值;
(Ⅲ)已知点H在棱上,且直线与直线所成角的余弦值为,求线段的长.
3.如图,在四棱锥中,平面平面,四边形为矩形,且,,、分别、的中点.
(1)证明:;
(2)设,点在线段上,且异面直线与所成角的余弦值为,求二面角的余弦值.
4.等边的边长为3,点,分别是,上的点,且满足.(如图(1)),将沿折起到的位置,使面平面,连接,(如图(2)).
(1)求证:平面;
(2)在线段上是否存在点,使直线与直线所成角的余弦值为?若存在,求出的值,若不存在,请说明理由.
练习二 已知线面角求其他量
5.如图,在正方体中,E为棱上一点.
(1)若E为棱的中点,求证:平面;
(2)若直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
6.如图,四棱锥中,,,且是边长为2的等边三角形.
(1)若,求证:;
(2)若平面平面ABCD,,直线SC与平面SAB所成角的正弦值为,求三棱锥的体积.
7.在正四棱柱中,,E为的中点.(用向量的方法证明)
(1)求证:平面.(用向量的方法证明)
(2)若F为上的动点,使直线与平面所成角的正弦值是,求BF的长.
8.如图,在五棱锥中,平面平面,是等边三角形,点、分别为和的中点,,,.
(1)求证:平面;
(2)求平面与平面的夹角的余弦值;
(3)设是线段上的动点,若直线与平面所成角的正弦值为,求线段的长.
练习三 已知二面角求其他量
9.如图,在四棱锥P—ABCD中,已知PC⊥底面ABCD,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是PB上一点.
(1)求证:平面EAC⊥平面PBC;
(2)若E是PB的中点,且二面角P—AC—E的余弦值是,求直线PA与平面EAC所成角的正弦值.
10.如图,在四棱柱中,底面ABCD,底面ABCD是直角梯形,,,,E是PD的中点.
(1)求证:平面平面PDC;
(2)若二面角的余弦值为,求直线PA与平面EAC所成角的正弦值.
11.如图四棱锥P - ABCD中,面PDC⊥面ABCD,∠ABC = ∠DCB = ,CD = 2AB = 2BC = 2,△PDC是等边三角形.
(1)设面PAB面PDC = l,证明:l//平面ABCD;
(2)线段PC内是否存在一点E,使面ADE与面ABCD所成角的余弦值为,如果存在,求λ = 的值,如果不存在,请说明理由.
12.如图,在三棱锥中,,平面,,分别为棱,的中点.
(1)求证:;
(2)若,,二面角的大小为,求三棱锥的体积.
第三篇 立体几何
专题04 立体几何中的由夹角求其他量问题
常见考点
考点一 已知线线角求其他量
典例1.如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AB⊥A1C;
(2)在棱AA1上是否存在一点F,使得异面直线AC1与BF所成角为60°,若存在,求出AF长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,3.
【解析】
【分析】
(1)由已知的数据可得BC²=AB²+AC²,从而得AB⊥AC,再由面ABC⊥平面AA1C1C,可得AB⊥平面AA1C1C,进而可证得AB⊥A1C;
(2)如图,以A为坐标原点,AC,AB,AA1分别为x,y,z轴建立空间直角坐标系,然后利用空间向量求解即可
【详解】
(1)证明:因为AA1C1C是边长为4的正方形,所以AC=4,又AB=3,BC=5,
所以BC²=AB²+AC²,所以AB⊥AC,
因为平面ABC⊥平面AA1C1C,平面ABC∩平面AA1C1C=AC,AB⊂平面ABC,
所以AB⊥平面AA1C1C,因为A1C⊂面AA1C1C,
所以AB⊥A1C.
(2)如图,以A为坐标原点,AC,AB,AA1分别为x,y,z轴建立空间直角坐标系,
则A(0,0,0),C1(4,0,4),B(0,3,0),设F(0,0,a),
则(4,0,4),(0,﹣3,a),0<a≤4,
因为异面直线AC1与BF所成角为60°,
所以|cs,|,
解得a=3,所以F(0,0,3),
则AF=3,
所以在棱AA1上存在一点F,使得异面直线AC1与BF所成角为60°,此时AF=3.
变式1-1.如图:在三棱锥中,底面,,点,,分别为棱,,的中点,是线段的中点,,.
(1)求证:平面;
(2)已知点在棱上,且直线与直线所成角的余弦值为,求线段的长.
【答案】(1)证明见解析;(2)或.
【解析】
【分析】
(1)取中点,连接、,则由三角形中位线定理可得,,由线面平行的判定定理可得平面,平面,再由面面平行的判定定理可得平面平面,从而可证得平面;
(2)如图建立空间直角坐标系,设,则,利用空间向量求解即可
【详解】
(1)证明:取中点,连接、,
∵为中点,∴,
∵平面,平面,
∴平面.
∵为中点,
∴,
又、分别为、的中点,
∴,则.
∵平面,平面,
∴平面.
又,、平面.
∴平面平面,
∵平面
∴平面;
(3)解:因为底面,平面,平面,
所以,
因为,
所以以为原点,分别以所在的直线为轴建立空间直角坐标系,如图所示,则,
,
依题意,设,则,
进而可得,.
由已知,得,
整理得,解得或,
所以线段的长为或.
变式1-2.如图,在四棱锥中,侧面是等边三角形且垂直于底面,底面是矩形,,是的中点.
(1)证明:平面;
(2)点在棱上,且直线与直线所成角的余弦值为,求二面角的余弦值.
【答案】(1)见证明;(2)
【解析】
【分析】
(1)证明CEAD,结合CEPD,即可证得平面.
(2)建立空间直角坐标系,分别求出各点坐标,由直线与直线所成角的余弦值为求得点F的坐标,再求出平面,平面的法向量,利用法向量夹角公式得解.
【详解】
(1)平面平面,平面平面,平面,
平面,又平面,.
侧面是等边三角形且是的中点
又
平面
(2)如图,以为原点,以为轴正方向,以为轴正方向,建立空间直角坐标系,则,,,,
,,
点在棱上,设,
则,
直线与直线所成角的余弦值为.
又,解得:
即为的中点
,,
设平面的法向量为,则
令,则
设平面的法向量为,则
令,则
二面角的余弦值为.
【点睛】
本题主要考查了线面垂直的判断,考查转化思想,还考查了平面法向量的求法、利用空间向量求二面角的平面角大小、利用向量求线线夹角,考查计算能力,属于基础题.
变式1-3.在如图所示的几何体中,四边形是正方形,四边形是梯形,,,平面平面,且.
(1)求证:平面;
(2)求平面与平面所成夹角的正切值;
(3)已知点在棱上,且异面直线与所成角的余弦值为,求线段的长.
【答案】(1)证明见解析;
(2)
(3)
【解析】
【分析】
先证明直线PD⊥平面ABCD.以点D为原点,分别以的方向为x轴,y轴,z轴的正向建立空间直角坐标系.
(1)利用向量法证明平面;
(2)利用向量法求平面与平面所成夹角,再求正切值;
(3)利用向量法求线段的长.
(1)
平面平面,平面ADPQ∩平面ABCD=AD.
而平面ADPQ,PD⊥AD,∴直线PD⊥平面ABCD.
由题意,以点D为原点,分别以的方向为x轴,y轴,z轴的正向建立如图空间直角坐标系.
则可得:.
显然::是平面PDC的一个法向量.
又,所以.
又∵直线平面PDC,∴平面.
(2)
.
设为平面PBC的一个法向量,则,
不妨设,可得.
设为平面PBQ的一个法向量,同理可求.
所以.
所以平面与平面所成夹角为.
而,所以平面与平面所成夹角的正切值.
(3)
设则, .
又,
∴,解得 (舍去),
故所求线段DH的长为.
考点二 已知线面角求其他量
典例2.已知梯形如图甲所示,其中,,,四边形是边长为1的正方形,沿将四边形折起,使得平面平面,得到如图乙所示的几何体.
(1)求证:平面;
(2)若点在线段上,且与平面所成角的正弦值为,求线段的长度.
【答案】(1)证明过程见解析;
(2).
【解析】
【分析】
(1)根据面面垂直的性质定理进行证明即可;
(2)建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
(1)
∵平面平面,平面
平面平面,,
∴平面;
(2)
(2)建系如图:
设平面的法向量,,,,
,
,则,
设,,
,
解得或(舍),
,∴.
变式2-1.如图甲,正方形边长为12,,,,分别交,于点,,将正方形沿,折叠使得与重合,构成如图乙所示的三棱柱,点在该三棱柱底边上.
(1)若,证明:平面;
(2)若直线与平面所成角的正弦值为,求的长.
【答案】(1)证明见解析;(2)或.
【解析】
【分析】
(1)在图乙中,过作,交于,连接,证明四边形为平行四边形,然后得到即可;
(2)分别以,,为,,轴,建立空间直角坐标系,然后算出平面的法向量坐标,设,得,然后由条件建立方程求解即可.
【详解】
(1)证明:在图乙中,过作,交于,连接,
则,∴共面且平面交平面于,
∵,,
∴,又为正方形,
,,由,有,
∴四边形为平行四边形,∴,
又平面,平面,
∴平面.
(2)由(1),,∴.
由题图知,,,分别以,,为,,轴,建立空间直角坐标系,
则,,,,
,,,
设平面的法向量为,
则
令,得,
设,得,
∵直线与平面所成角的正弦值为,
∴,
解得或,即或.
变式2-2.如图,三棱柱所有的棱长为2,,M是棱BC的中点.
(Ⅰ)求证:平面ABC;
(Ⅱ)在线段B1C是否存在一点P,使直线BP与平面A1BC 所成角的正弦值为? 若存在,求出CP的值; 若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)存在,.
【解析】
【分析】
(1)由题意,证明与,根据线面垂直的判定定理即可证明平面;
(2)建立恰当的空间直角坐标系,令,求出所需点的坐标,向量的坐标,法向量的坐标,根据向量法求解线面角即可.
【详解】
解:(1)证明:,,是中点,
,
又,
,
,
平面,
(2)建立如图所示的空间直角坐标系,
由(1)知平面A1BC的法向量为,,,,,,
令,
则,
设直线BP与平面A1BC 所成角为,则
,
解得或(舍),
所以当时,满足题意,此时.
变式2-3.如图所示,四棱锥中,菱形所在的平面,,点、分别是、的中点,是线段上的点.
(1)求证:平面平面;
(2)当时,是否存在点,使直线与平面所成角的正弦值为?若存在,请求出的值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,.
【解析】
【分析】
(1)根据菱形的性质,结合平行线的性质、线面垂直的判定定理、面面垂直的判定定理进行证明即可;
(2)建立空间直角坐标系,利用空间平面向量夹角公式,结合线面角的定义进行求解即可.
【详解】
(1)证明:连接因为底面为菱形,,
所以是正三角形,
∵是的中点,∴,
又,∴,
∵平面,平面,∴,
又,∴平面,
又平面,所以平面平面.
(2)解:以为坐标原点建立如图所示空间直角坐标系,
不妨设,则,
,,,,,
设
则
设平面的一个法向量为,
则
取,则,
得
设直线与平面所成角为,
化简得:,则
故存在点满足题意,此时.
考点三 已知二面角求其他量
典例3.如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC.
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)先证明垂直于,再通过线线垂直推证线面垂直即可;
(2)以为坐标原点,建立空间直角坐标系,由二面角M-PA-C为30°求得点的坐标,再用向量法求线面角的正弦值即可.
(1)
连接如下所示:
因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2.
因为AB=BC=,故可得,
所以△ABC为等腰直角三角形,且OB⊥AC,OB=AC=2.
由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC,OB∩AC=O,面,
知PO⊥平面ABC.
(2)
根据(1)中所证可知,两两垂直,连接OM,故以O为坐标原点,
的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向,
建立空间直角坐标系如下所示:
由已知得O=,
取平面PAC的法向量=.设M,则=.
设平面PAM的法向量为
由·=0,·=0得,可取=(),
所以cs=;由已知得|cs|==.
解得a=(舍去),a=.所以n=.
又=,所以cs=.
所以PC与平面PAM所成角的正弦值为.
变式3-1.如图1,平面图形PABCD由直角梯形ABCD和拼接而成,其中,、,,,PC与AD相交于O,现沿着AD折成四棱锥(如图2).
(1)当四棱锥的体积最大时,求点B到平面PCD的距离;
(2)在(1)的条件下,线段PD上是否存在一点Q,使得二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.
【答案】(1);
(2)存在,.
【解析】
【分析】
(1)根据面面垂直的性质,建立空间直角坐标系,利用空间距离公式进行求解即可;
(2)利用空间夹角公式进行求解即可.
(1)
在图1中,在中,,,∴.
易知四边形ABCO为正方形,∴,即O为AD的中点,
在图2中,当四棱锥的体积最大时,
侧面底面ABCD,此时平面ABCD,
以O为坐标原点,OC所在直线为x轴,OD所在直线为y轴,OP所在直线为z轴建立空间直角坐标系,如图所示,则,,,,,
∴,,.
设平面PCD的一个法向量为,
则
取,得.
则B点到平面PCD的距离.
(2)
假设存在,且设.
∵,∴,∴,
∴.
设平面CAQ的一个法向量为,又,,
则
取,得.
又易知平面CAD的一个法向量为,
∵二面角的余弦值为,
∴,
整理化简,得,解得或(舍去).
∴线段PD上存在满足题意的点Q,且.
变式3-2.如图,在三棱锥中,平面ABC,,,于点D,点E在侧棱PC上,且.
(1)证明:平面ACD;
(2)是否存在λ,使二面角的余弦值为?若存在,求出λ的值;若不存在,说明理由.
【答案】(1)证明见解析
(2)存在;
【解析】
【分析】
(1)根据线面垂直的判定定理,结合线面垂直的性质进行证明即可;
(2)建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
(1)
证明:∵平面ABC,∴,又∵,,
∴平面PBC,∴,又∵,,∴平面ACD.
(2)
如图建系,不妨设,∴,,,
∴,,,,
,,,
设平面CAD和平面ADE的一个法向量分别为,,
∴,
设二面角的平面角为θ,,所成角为φ,
∴.
,故存在,.
变式3-3.如图,四棱柱ABCD—A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
(1)求证:平面CC1D1D⊥底面ABCD;
(2)若平面BCC1B1与平面BED1所成的锐二面角的大小为,求线段ED1的长度.
【答案】(1)证明见解析;(2).
【解析】
【分析】
(1)利用线面垂直的判定定理证明AD⊥平面CDD1C1,可得AD⊥D1E,又CD⊥D1E,即可证明D1E⊥平面ABCD,再由面面垂直的判定定理证明即可;
(2)D1E=a,建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式列出关于a的方程求解即可.
【详解】
(1)证明:因为底面ABCD和侧面BCC1B1都是矩形,
所以AD⊥CD,AD⊥DD1,
又CD∩DD1=D,CD,DD1⊂平面CDD1C1,
所以AD⊥平面CDD1C1,又D1E⊂平面CDD1C1,
所以AD⊥D1E,又CD⊥D1E,且CD∩AD=D,CD,AD⊂平面ABCD,
故D1E⊥平面ABCD,又D1E⊂平面CC1D1D,
则平面CC1D1D⊥平面ABCD;
(2)解:取AB得中点F,连结EF,则四边形EFBC为正方形,
所以EF⊥CD,故以E为坐标原点,建立空间直角坐标系如图所示,
设D1E=a,则E(0,0,0),F(1,0,0),B(1,1,0),C(0,1,0),C1(0,2,a),
所以,
设平面BCC1B1的法向量为,
则有,即,
令z=1,则,
因为FC⊥BE,又FC⊥D1E,BE∩D1E=E,BE,D1E⊂平面BED1,
所以FC⊥平面BED1,
故为平面BD1E的一个法向量,
所以,
因为平面BCC1B1与平面BED1所成的锐二面角的大小为,
,解得a=1,
所以D1E=1.
巩固练习
练习一 已知线线角求其他量
1.已知正方形和矩形所在的平面互相垂直,且,,点是线段中点.
(1)求证:平面;
(2)求平面和平面的锐二面角的余弦值;
(3)线段上是否存在点,使得与所成的角为?若存在,请求出的长,若不存在,请说明理由.
【答案】(1)见解析;(2);(3)存在,.
【解析】
【分析】
(1)记与的交点为,连接,得四边形是平行四边形,则,再由直线与平面平行的判定可得平面;
(2)在平面中过作于,连接,说明是平面和平面的角平面角或补角,然后平面和平面夹角的余弦值;
(3)建立空间直角坐标系,设出线段上点的坐标,由与所成的角是,转化为向量的夹角求解.
【详解】
(1)证明:记与的交点为,连接,
、分别是、的中点,是矩形,
四边形是平行四边形,则
平面,平面,
平面;
(2)解:在平面中,过作于,连接,
,,,
平面,
是在平面上的射影,
是平面和平面的夹角的平面角,
在中,,,
平面和平面的锐二面角的余弦值为;
(3)解:建立如图所示空间直角坐标系,
则,0,,,1,,,1,,
设,,,
则,,
由与所成的角恰为,得,
即,解得或(舍.
,则.
故线段上存在点,使得与所成的角恰为,此时.
2.如图,在三棱锥中,底面.点D,E,N分别为棱的中点,M是线段的中点,,.
(Ⅰ)求证:平面;
(Ⅱ)求二面角的正弦值;
(Ⅲ)已知点H在棱上,且直线与直线所成角的余弦值为,求线段的长.
【答案】(Ⅰ)证明见解析;(Ⅱ) ;(Ⅲ)或1.
【解析】
【分析】
本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.首先要建立空间直角坐标系,写出相关点的坐标,证明线面平行只需求出平面的法向量,计算直线对应的向量与法向量的数量积为0,求二面角只需求出两个半平面对应的法向量,借助法向量的夹角求二面角,利用向量的夹角公式,求出异面直线所成角的余弦值,利用已知条件,求出的值.
【详解】
(Ⅰ)如图所示建立空间直角坐标系.
则,
证明:.设为平面的法向量,
则,即.不妨设,可得 ,
又,
可得.因为平面,
所以平面 ,
(Ⅱ)解:易知为平面的一个法向量.
设为平面的法向量,则,
因为,,所以.
不妨设,可得 ,
因此有,
于是.
所以,二面角的正弦值为 ;
(Ⅲ)依题意,设,
则,
进而可得,
由已知,得,
整理得,
解得,或.
所以,线段的长为或1
【点睛】
本题考查直线与平面平行、二面角、异面直线所成的角.空间向量是解决空间几何问题的锐利武器,不论是求空间角、空间距离还是证明线面关系利用空间向量都很方便,利用向量夹角公式求异面直线所成的角又快又准,特别是借助平面的法向量求线面角,二面角或点到平面的距离都很容易.
3.如图,在四棱锥中,平面平面,四边形为矩形,且,,、分别、的中点.
(1)证明:;
(2)设,点在线段上,且异面直线与所成角的余弦值为,求二面角的余弦值.
【答案】(1)证明见解析;(2).
【解析】
【分析】
(1)证明出平面,可得出,利用正弦定理可证明出,利用线面垂直的判定定理可得出平面,由此可证得结论成立;
(2)以点为坐标原点,以、、方向为、、轴的正方向,建立空间直角坐标系,根据已知条件求出点的坐标,再利用空间向量法可求得二面角的余弦值.
【详解】
(1)在中,根据正弦定理有,即,
得,即,所以.
因为平面平面,平面平面,平面,,
所以平面,
又因为平面,所以.
又因为平面,平面,,所以平面,
又因为平面,所以;
(2)如图,以为坐标原点,
以、、方向为、、轴的正方向,建立空间直角坐标系.
则、、、、、、,
设,,,
即,得,
所以,,
,
化简得,解得或(舍),
所以,,,
设平面的法向量,则,
取,可得,
,
设平面的法向量为,则,
取,可得,
设二面角的平面角为,则为锐角,
则,即二面角的余弦值为.
4.等边的边长为3,点,分别是,上的点,且满足.(如图(1)),将沿折起到的位置,使面平面,连接,(如图(2)).
(1)求证:平面;
(2)在线段上是否存在点,使直线与直线所成角的余弦值为?若存在,求出的值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,.
【解析】
(1)由已知条件推导出,从而得到,折叠后有,由此能够证明平面;
(2)由(1)知,平面,以为坐标原点,以射线、、分别为轴、轴、轴的正半轴建立空间直角坐标系,可求得,,由题意根据两向量的夹角公式即可求解.
【详解】
(1)证明:题图(1)中,由已知可得:
,,.
从而
故得,所以,.
所以题图(2)中,,,
∵面面
面面
面
∴面
(2)解:存在.由(1)知,平面.
以为坐标原点,以射线、、分别为轴、轴、轴的正半轴建立空间直角坐标系,如图,
,,,
∴
,
∴
∴.
【点睛】
思路点睛:该题考查的是有关立体几何的问题,解题思路如下:
(1)利用面面垂直的性质,结合线线垂直的条件,证得线面垂直;
(2)结合(1)的条件,建立空间直角坐标系,假设存在对应的点P,设,利用空间向量解决线线角的余弦值,建立关于的关系式,求得结果.
练习二 已知线面角求其他量
5.如图,在正方体中,E为棱上一点.
(1)若E为棱的中点,求证:平面;
(2)若直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】
(1)利用线面平行的判定定理即可证明;
(2)以A为原点,AD,AB,所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,用向量法求解.
(1)
在正方体中,,,
所以四边形为平行四边形,故,
又平面,平面.所以平面.
(2)
设正方体的棱长为2,.
以A为原点,AD,AB,所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则,,,,则,,.
设平面的一个法向量为,
由即,不妨令,得.
设直线与平面所成的角为,
则,解得,
所以平面的法向量为.
由题知,平面的法向量,
所以,
所以平面与平面所成锐二面角的余弦值为.
6.如图,四棱锥中,,,且是边长为2的等边三角形.
(1)若,求证:;
(2)若平面平面ABCD,,直线SC与平面SAB所成角的正弦值为,求三棱锥的体积.
【答案】(1)证明见解析
(2)
【解析】
【分析】
(1)由题目证明平面SOC,利用线面垂直的性质定理即可证明;
(2)建立直角坐标系,设,运用向量的夹角公式求出直线SC与平面SAB所成角的正弦值即可求出,进而求出体积.
(1)
如图,取AD的中点O,连接SO,CO.
因为为等边三角形,所以.
因为,,,,
所以四边形ABCO为矩形,
所以.
因为SO,平面SOC,且,
所以平面SOC,因为平面SOC,所以.
(2)
因为平面平面ABCD,平面平面,平面ABCD,,,所以平面ABCD,平面SAD,
故以点A为坐标原点,AB,AD所在直线分别为x,y轴建立如图所示的空间直角坐标系,
则由题意知,,,
所以,.
设平面SAB的法向量为,
则,即,则,取,得,故.
设,则,,
则,得,即,
故.
7.在正四棱柱中,,E为的中点.(用向量的方法证明)
(1)求证:平面.(用向量的方法证明)
(2)若F为上的动点,使直线与平面所成角的正弦值是,求BF的长.
【答案】(1)证明见解析
(2)1
【解析】
【分析】
建立如图所示空间直角坐标系,
(1)求出平面的法向量,利用证明即可;
(2)设点的坐标为,由线面角公式可求出,即可利用向量的模求的长.
(1)
由题意可知,以为坐标原点,建立如图示的空间直角坐标系.
,,,,,,
证明:设平面的法向量,
,,
由,即
取,得,
又,
因为,所以,
所以平面.
(2)
设点的坐标为,
,由(1)知,,
设直线与平面所成角为,则
,解得.
所以点F的坐标为,,,
所以的长为.
8.如图,在五棱锥中,平面平面,是等边三角形,点、分别为和的中点,,,.
(1)求证:平面;
(2)求平面与平面的夹角的余弦值;
(3)设是线段上的动点,若直线与平面所成角的正弦值为,求线段的长.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】
(1)推导出平面,,然后点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间向量法可证得结论成立;
(2)利用空间向量法可求得平面与平面的夹角的余弦值;
(3)设点,其中,根据已知条件结合空间向量法可得出关于的方程,解出的值,即可得解.
(1)
证明:因为是等边三角形,为的中点,则,
因为平面平面,平面平面,平面,
所以,平面,
,,则,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、、、、,
设平面的法向量为,,,
由,取,可得,
,则,则,
平面,故平面.
(2)
解:设平面的法向量为,,,
由,取,可得,
,
因此,平面与平面的夹角的余弦值为.
(3)
解:设点,其中,则,
由已知可得,
整理可得,因为,解得,因此,.
练习三 已知二面角求其他量
9.如图,在四棱锥P—ABCD中,已知PC⊥底面ABCD,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是PB上一点.
(1)求证:平面EAC⊥平面PBC;
(2)若E是PB的中点,且二面角P—AC—E的余弦值是,求直线PA与平面EAC所成角的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】
(1)设AB的中点为G,连接CG,易得四边形ADCG为边长为1的正方形,得到,再由,从而证得平面PBC,再利用面面垂直的判定定理证明;
(2)建立空间直角坐标,设 ,易知 为 平面 PAC的一个法向量,再求得平面EAC的一个法向量 ,由,求得 ,从而得到 求解.
(1)
证明:如图所示:
因为PC⊥底面ABCD,AC底面ABCD,
所以,又,在中,,
设AB的中点为G,连接CG,则四边形ADCG为边长为1的正方形,
所以,且,
则,所以,又,
所以平面PBC,又平面EAC,
所以平面EAC⊥平面PBC;
(2)
建立如图所示空间直角坐标系:
则,
设 ,则 ,
所以 ,
因为 ,
所以 平面PAC,则 为 平面 PAC的一个法向量,
设平面EAC的一个法向量为 ,
则 ,即 ,
令 ,则 ,
所以 ,
解得 ,则 ,
设直线PA与平面EAC所成的角为 ,
则 ,
所以 直线PA与平面EAC所成的角的正弦值为.
10.如图,在四棱柱中,底面ABCD,底面ABCD是直角梯形,,,,E是PD的中点.
(1)求证:平面平面PDC;
(2)若二面角的余弦值为,求直线PA与平面EAC所成角的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】
(1)根据线面垂直的性质可得,利用勾股定理的逆定理可得,结合线面垂直的判定定理可得平面PDC.即可证明;
(2)建立如图空间直角坐标系,设,利用向量法求出平面PAC和平面EAC的法向量,根据二面角的余弦值和空间向量数量积的定义求出,再次利用空间向量的数量积计算,直接得出结果.
(1)
∵平面ABCD,平面ABCD,∴.
∵,,∴.
∴,∴.
又平面PDC,平面PDC,,
∴平面PDC.
∵平面EAC,∴平面平面PDC;
(2)
由(1)知,,又平面ABCD,故以C为坐标原点,,,的方向分别为x轴、y轴、z轴正方向,建立空间直角坐标系,如图所示,
则,,,
设,则,,,,.
取,则,所以为平面PAC的一个法向量.
设为平面EAC的法向量,
则,即,
则,取,则,,
依题意,,
则,于是,,
设直线PA与平面EAC所成的角为,
则,
即直线PA与平面EAC所成角的正弦值为.
11.如图四棱锥P - ABCD中,面PDC⊥面ABCD,∠ABC = ∠DCB = ,CD = 2AB = 2BC = 2,△PDC是等边三角形.
(1)设面PAB面PDC = l,证明:l//平面ABCD;
(2)线段PC内是否存在一点E,使面ADE与面ABCD所成角的余弦值为,如果存在,求λ = 的值,如果不存在,请说明理由.
【答案】(1)证明见解析
(2)存在
【解析】
【分析】
(1)由已知可得∥,再由线面平行的判定可得∥平面,再由线面平行的性质可得∥,再由线面平行的判定可得结论,
(2)由已知条件可证得两两垂直,所以以为原点,所在的直线分别为轴建立空间直角坐标系,利用空间向量求解
(1)
证明:因为,
所以,所以∥,
因为平面,平面,
所以∥平面,
因为平面,且平面面,
所以∥,
因为平面,平面,
所以∥平面,
(2)
设的中点为,
因为△PDC是等边三角形,所以,
因为平面PDC⊥平面ABCD,且平面面,
所以平面,
因为平面,
所以,
所以以为原点,所在的直线分别为轴建立空间直角坐标系,如图所示,
则,所以,
假设存在这样的点,由已知得,则,
所以,
因为平面,所以平面的一个法向量为,
设平面的一个法向量为,则
,令,则,则
所以,
整理得,解得(舍去),或,
所以
12.如图,在三棱锥中,,平面,,分别为棱,的中点.
(1)求证:;
(2)若,,二面角的大小为,求三棱锥的体积.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)利用线面垂直的判定定理及性质即证;
(2)利用坐标法,结合条件可求,然后利用体积公式即求.
(1)
,是的中点,
,
平面,平面,
,又,
平面,
平面,
;
(2)
,,
,
取的中点,连接,则,
平面,
以为坐标原点,分别以、、所在直线为、、轴建立空间直角坐标系,
设,则,,,,
,,,,
设平面的一个法向量为,
由,取,得;
设平面的一个法向量为,
由,取,得,
∵二面角的大小为,
,解得,
,
则三棱锥的体积.
相关试卷
这是一份备战2024年高考数学二轮复习专题03立体几何中的夹角问题(原卷版+解析),共56页。试卷主要包含了线线角,线面角,二面角等内容,欢迎下载使用。
这是一份备战2024年高考数学二轮复习专题03立体几何中的夹角问题(原卷版+解析),共56页。试卷主要包含了线线角,线面角,二面角等内容,欢迎下载使用。
这是一份备战2024年高考数学二轮复习专题03解析几何中的定点问题(原卷版+解析),共31页。试卷主要包含了直线恒过定点,平面内的定点等内容,欢迎下载使用。









