备战2024年高考数学二轮复习专题05立体几何中的距离问题(原卷版+解析)

这是一份备战2024年高考数学二轮复习专题05立体几何中的距离问题(原卷版+解析)，共44页。试卷主要包含了点面、线面、面面距离，点线、线线距离等内容，欢迎下载使用。
常见考点
考点一 点面、线面、面面距离
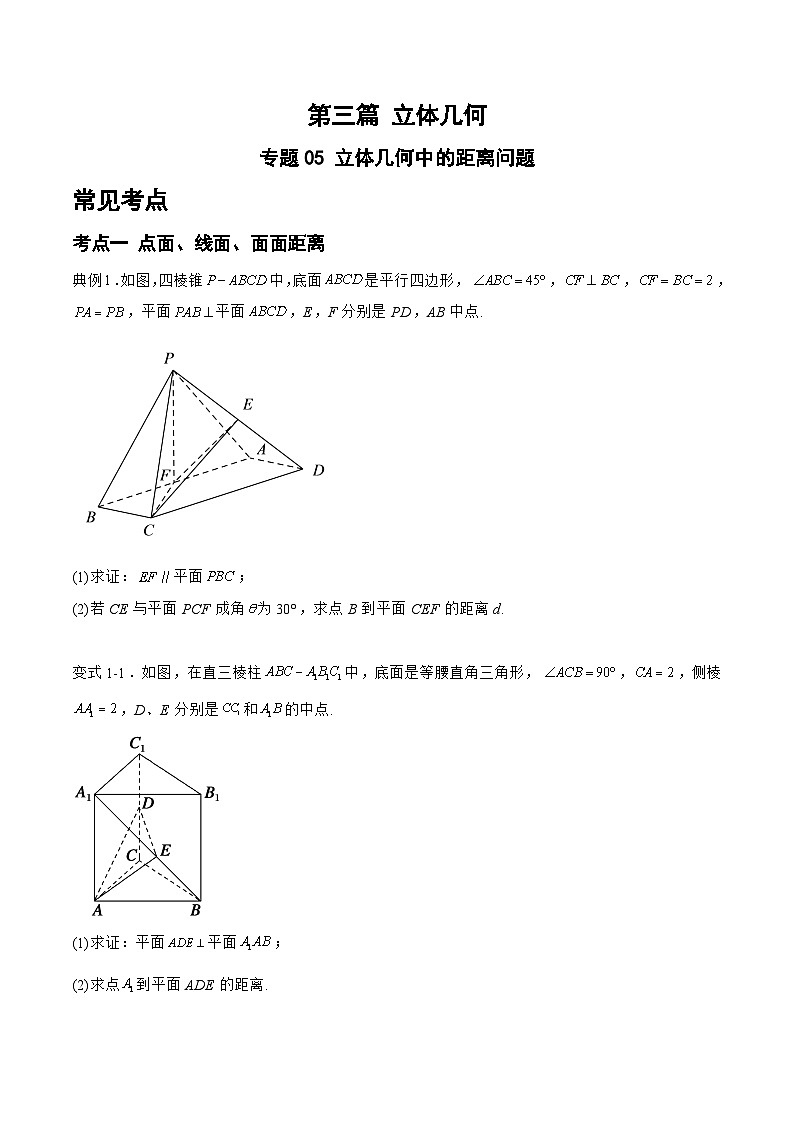
典例1．如图，四棱锥中，底面是平行四边形，，，，，平面平面，E，F分别是PD，AB中点.
(1)求证：平面；
(2)若CE与平面PCF成角为30°，求点B到平面CEF的距离d.
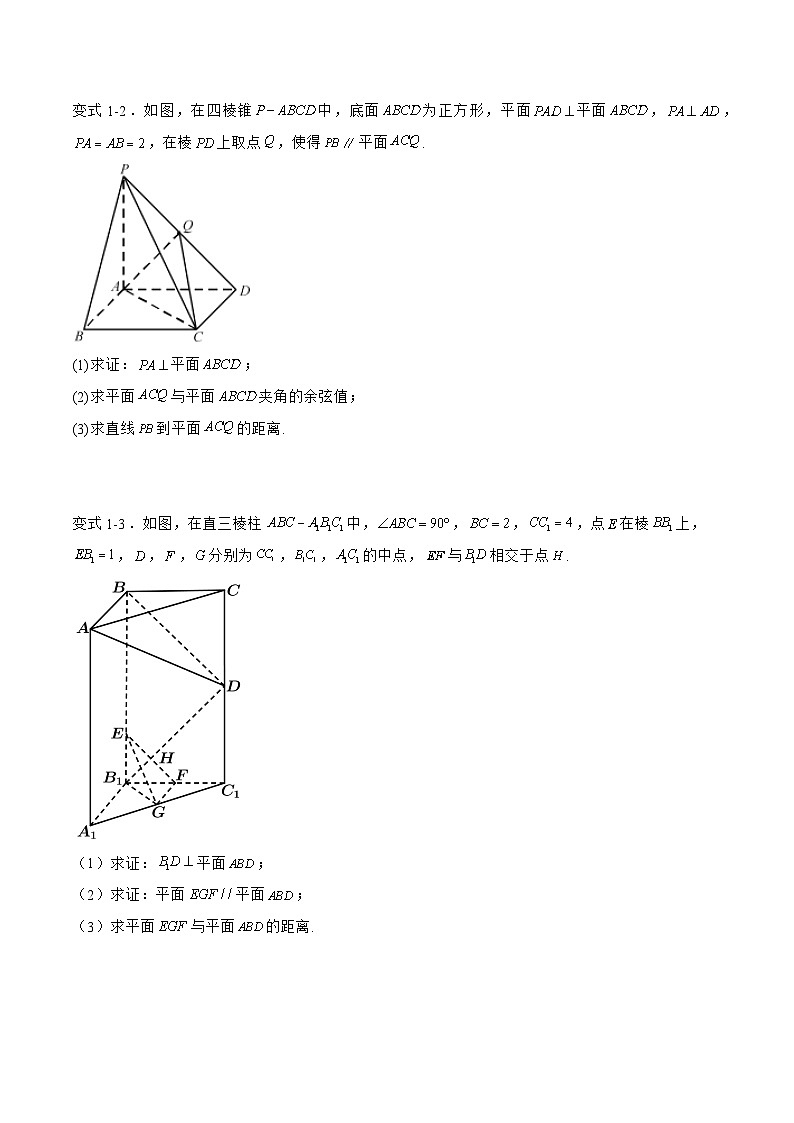
变式1-1．如图，在直三棱柱中，底面是等腰直角三角形，，，侧棱，D、E分别是和的中点.
(1)求证：平面平面；
(2)求点到平面ADE的距离.
变式1-2．如图，在四棱锥中，底面为正方形，平面平面，，，在棱上取点，使得平面.
(1)求证：平面；
(2)求平面与平面夹角的余弦值；
(3)求直线到平面的距离.
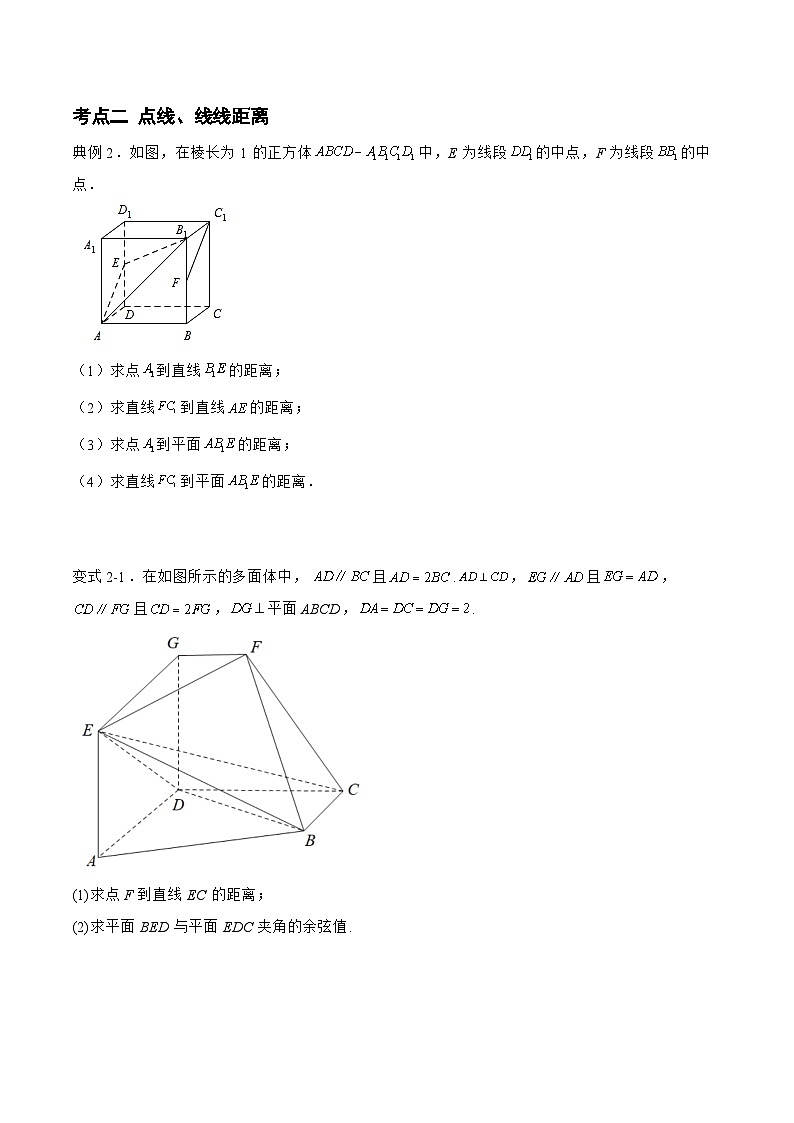
变式1-3．如图，在直三棱柱中，，，，点在棱上，，，，分别为，，的中点，与相交于点.
（1）求证：平面；
（2）求证：平面平面；
（3）求平面与平面的距离.
考点二 点线、线线距离
典例2．如图，在棱长为1的正方体中，E为线段的中点，F为线段的中点．
（1）求点到直线的距离；
（2）求直线到直线的距离；
（3）求点到平面的距离；
（4）求直线到平面的距离．
变式2-1．在如图所示的多面体中，且.，且，且，平面ABCD，.
(1)求点F到直线EC的距离；
(2)求平面BED与平面EDC夹角的余弦值.
变式2-2．如图，在正四棱柱ABCD﹣A1B1C1D1中，AB＝1，AA1＝2，点E为CC1中点，点F为BD1中点．
（1）求异面直线BD1与CC1的距离；
（2）求直线BD1与平面BDE所成角的正弦值；
（3）求点F到平面BDE的距离．
变式2-3．如图，三棱柱中，侧面底面，是边长为2的正三角形，已知点满足.
（1）求二面角的大小；
（2）求异面直线与的距离；
（3）直线上是否存在点，使平面？若存在，请确定点的位置；若不存在，请说明理由.
巩固练习
练习一 点面、线面、面面距离
1．如图，直三棱柱中，，，，且.
(1)求平面BDC与平面所成角的余弦值；
(2)求点到平面BDC距离.
2．如图，在四棱锥中，底面ABCD为矩形且，侧面底面ABCD，且侧面PAD是正三角形，E､F分别是AD，PB的中点.
(1)求证：平面PCE；
(2)求直线CF与平面PCE所成角的正弦值；
(3)求点F到平面PCE的距离.
3．如图在直三棱柱中，为的中点，为的中点，是中点，是与的交点，是与的交点.
(1)求证：；
(2)求证：平面；
(3)求直线与平面的距离.
4．如图，正方体ABCD­A1B1C1D1的棱长为1， M， N分别是BB1， B1C1的中点．
(1)求直线MN到平面ACD1的距离；
(2)若G是A1B1的中点，求平面MNG与平面ACD1的距离．
练习二 点线、线线距离
5．已知三棱柱的侧棱垂直于底面，，，分别是棱的中点.
(1)求证：平面；
(2)求点到直线的距离.
6．已知四棱锥中，底面ABCD是矩形，平面ABCD，，，点M在PD上，且.
(1)求的值；
(2)求点B到直线CM的距离.
7．如图，在四棱锥中，底面ABCD为矩形，底面ABCD，E是AB上一点，.已知，，.
（1）求直线AD与平面PBC间的距离；
（2）求异面直线EC与PB间的距离；
（3）求点B到平面PEC的距离.
8．如下图，在四棱锥中，已知平面，且四边形为直角梯形，．
（1）求平面与平面所成夹角的余弦值；
（2）求异面直线与之间的距离．
第三篇 立体几何
专题05 立体几何中的距离问题
常见考点
考点一 点面、线面、面面距离
典例1．如图，四棱锥中，底面是平行四边形，，，，，平面平面，E，F分别是PD，AB中点.
(1)求证：平面；
(2)若CE与平面PCF成角为30°，求点B到平面CEF的距离d.
【答案】(1)证明过程见解析
(2)
【解析】
【分析】
（1）作出辅助线，构造平行四边形，证明线线平行，进而证明线面平行；（2）建立空间直角坐标系，利用空间向量进行求解.
(1)
取PC中点G，连接EG，BG，因为E是PD中点，所以EG是三角形PCD的中位线，所以EG∥CD且EG=CD，又因为F是AB中点，四边形ABCD是平行四边形，所以BF∥CD，BF=AB，故EG∥BF，EG=BF，所以四边形BFEG是平行四边形，所以EF∥BG，因为EF平面PBC，BG平面PBC，所以平面.
(2)
因为，F是AB中点，所以PF⊥AB，因为平面平面，交线为AB，所以PF⊥平面ABCD，因为，所以以F为坐标原点，FC所在直线为x轴，过点F平行于BC的直线为y轴，FP所在直线为z轴建立空间直角坐标系，，，则，，，，设（），则，，其中平面PCF的法向量设为，则，解得：，，
设平面CEF的法向量为，则，解得：，设，则，所以，则
变式1-1．如图，在直三棱柱中，底面是等腰直角三角形，，，侧棱，D、E分别是和的中点.
(1)求证：平面平面；
(2)求点到平面ADE的距离.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）建立空间直角坐标系，利用向量证明，然后可证；
（2）求出法向量，然后根据点到平面的距离向量公式可得.
(1)
易知、、两两垂直，于是如图建立空间直角坐标系
则、、、、、
所以、、、、
因为，
所以
又因为平面，平面
所以平面
又平面
所以平面平面
(2)
设平面的法向量为
则，取得
则点到平面ADE的距离
变式1-2．如图，在四棱锥中，底面为正方形，平面平面，，，在棱上取点，使得平面.
(1)求证：平面；
(2)求平面与平面夹角的余弦值；
(3)求直线到平面的距离.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】
（1）根据面面垂直的性质定理证得结论成立.
（2）判断出点的位置，建立空间直角坐标系，利用向量法求得平面与平面夹角的余弦值.
（3）利用向量法求得直线到平面的距离.
(1)
由于平面平面，且交线为，
平面，，
所以平面.
(2)
设，连接，
由于平面，平面，平面平面，
所以，由于是的中点，所以是的中点.
由于平面，所以，
故两两垂直，以为原点建立空间直角坐标系，如图所示，
，
设平面的法向量为，
所以，故可设，
平面的法向量为，
平面与平面夹角为，
则.
(3)
由于平面，则到平面的距离，即到平面的距离.
,
到平面的距离为.
即直线到平面的距离为.
变式1-3．如图，在直三棱柱中，，，，点在棱上，，，，分别为，，的中点，与相交于点.
（1）求证：平面；
（2）求证：平面平面；
（3）求平面与平面的距离.
【答案】（1）证明见解析；（2）证明见解析；（3）.
【解析】
【分析】
（1）建立空间直角坐标系，利用向量法证得平面.
（2）利用向量法证得平面平面.
（3）利用向量法求得平面与平面的距离.
【详解】
（1）设，建立如图所示空间直角坐标系，
，
，
，
所以，
即，所以平面.
（2），
，
即，所以平面.
所以平面平面.
（3）由（2）可知平面平面，平面，平面.
，
所以平面与平面的距离为.
考点二 点线、线线距离
典例2．如图，在棱长为1的正方体中，E为线段的中点，F为线段的中点．
（1）求点到直线的距离；
（2）求直线到直线的距离；
（3）求点到平面的距离；
（4）求直线到平面的距离．
【答案】（1）；（2）；（3）；（4）.
【解析】
【分析】
（1）建立坐标系，求出向量在单位向量上的投影，结合勾股定理可得点到直线的距离；
（2）先证明再转化为点到直线的距离求解；
（3）求解平面的法向量，利用点到平面的距离公式进行求解；
（4）把直线到平面的距离转化为到平面的距离，利用法向量进行求解.
【详解】
建立如图所示的空间直角坐标系，
则
（1）
因为，
所以.
所以点到直线的距离为.
（2）因为所以，即
所以点到直线的距离即为直线到直线的距离.
所以直线到直线的距离为
（3）设平面的一个法向量为，
.
由
令，则，即.
设点到平面的距离为，
则，即点到平面的距离为.
（4）因为所以平面，
所以直线到平面的距离等于到平面的距离.
，由（3）得平面的一个法向量为，
所以到平面的距离为，
所以直线到平面的距离为.
变式2-1．在如图所示的多面体中，且.，且，且，平面ABCD，.
(1)求点F到直线EC的距离；
(2)求平面BED与平面EDC夹角的余弦值.
【答案】(1)
(2)
【解析】
【分析】
（1）根据线面垂直的性质可得，，以为坐标原点建立空间直角坐标系，代入即可；
（2）求出平面与平面的法向量，再利用向量的夹角公式即可得解.
(1)
因为平面，
平面，平面，
所以，且，
因为，
如图所示，以为坐标原点建立空间直角坐标系，
则，，，，，，，
所以，，
所以求点F到直线EC的距离为
.
(2)
，
设平面的法向量为，
则，即，
令，有，
设平面的法向量为，
则，即，
令，有，
设平面和平面的夹角为，
，
所以平面和平面的夹角的余弦值为．
变式2-2．如图，在正四棱柱ABCD﹣A1B1C1D1中，AB＝1，AA1＝2，点E为CC1中点，点F为BD1中点．
（1）求异面直线BD1与CC1的距离；
（2）求直线BD1与平面BDE所成角的正弦值；
（3）求点F到平面BDE的距离．
【答案】（1）；（2）；（3）．
【解析】
【分析】
（1）以D为原点，建立空间直角坐标系，由•0，•0，知EF为BD1与CC1的公垂线，再计算||，即可；
（2）求得平面BDE的法向量，设直线BD1与平面BDE所成角为θ，由sinθ＝|cs，|，即可得解；
（3）点F到平面BDE的距离为，代入相关数据，进行运算即可得解．
【详解】
（1）以D为原点，DA，DC，DD1所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，
则B（1，1，0），D1（0，0，2），C（0，1，0），C1（0，1，2），E（0，1，1），F（，，1），
∴（﹣1，﹣1，2），（0，0，2），（，，0），
∴•0，•0，
∴BD1⊥EF，CC1⊥EF，即EF为BD1与CC1的公垂线，
而||，
∴异面直线BD1与CC1的距离为．
（2）由（1）知，（1，1，0），（0，1，1），（﹣1，﹣1，2），
设平面BDE的法向量为（x，y，z），则，即，
令y＝1，则x＝﹣1，z＝﹣1，∴（﹣1，1，﹣1），
设直线BD1与平面BDE所成角为θ，
则sinθ＝|cs，|＝||＝||，
故直线BD1与平面BDE所成角的正弦值为．
（3）由（1）知，（，，1），
由（2）知，平面BDE的法向量为（﹣1，1，﹣1），
∴点F到平面BDE的距离为||．
变式2-3．如图，三棱柱中，侧面底面，是边长为2的正三角形，已知点满足.
（1）求二面角的大小；
（2）求异面直线与的距离；
（3）直线上是否存在点，使平面？若存在，请确定点的位置；若不存在，请说明理由.
【答案】（1）（2）（3）存在点，其坐标为，即恰好为点
【解析】
（1）建立空间直角坐标系，利用平面的法向量和平面的法向量，计算出二面角的余弦值，由此求得其大小.
（2）求得异面直线与的公垂线的方向向量，并由此计算出异面直线与的距离.
（3）根据求得点的坐标，设出点的坐标，根据、与平面的法向量垂直列方程组，解方程组求得点的坐标，由此判断出存在点符合题意.
【详解】
（1）侧面底面，又均为正三角形，取得中点，连接，，
则底面，
故以为坐标原点，分别以为轴、轴、轴建立如图所示空间直角坐标系，
则
设平面的法向量为
取，可得
又平面的一个法向量为
由图知二面角为锐角，故二面角的大小为.
（2）异面直线与的公垂线的方向向量，则
易得，异面直线与的距离
（3），而
又，点的坐标为
假设存在点符合题意，则点的坐标可设为
平面为平面的一个法向量，
由，得.
又平面，
故存在点，使平面，其坐标为，即恰好为点.
【点睛】
本小题主要考查利用空间向量法计算二面角、异面直线公垂线段的长，考查利用空间向量法研究线面平行的条件，考查数形结合的数学思想方法，考查空间想象能力，属于中档题.
巩固练习
练习一 点面、线面、面面距离
1．如图，直三棱柱中，，，，且.
(1)求平面BDC与平面所成角的余弦值；
(2)求点到平面BDC距离.
【答案】(1)
(2)
【解析】
【分析】
（1）以C为原点.的方向分别为x轴、y轴、z轴正方向，建立如图所示的空间直角坐标系，求得平面BDC的法向量与平面的法向量，利用数量积公式计算即可得出结果.
（2）利用向量公式计算即可得出结果.
(1)
依题意两两互相垂直，以C为原点.的方向分别为x轴、y轴、z轴正方向，建立如图所示的空间直角坐标系，则
设平面BDC的一个法向量为，则令，则得，此时.
设平面的一个法向量为则
令则得此时
因为,
所以平面BDC与平面所成角的余弦值为.
(2)
因为,
点到平面BDC距离为.
2．如图，在四棱锥中，底面ABCD为矩形且，侧面底面ABCD，且侧面PAD是正三角形，E､F分别是AD，PB的中点.
(1)求证：平面PCE；
(2)求直线CF与平面PCE所成角的正弦值；
(3)求点F到平面PCE的距离.
【答案】(1)证明见解析
(2)
(3)
【解析】
【分析】
（1）作出辅助线，证明线线平行，进而证明出线面平行；（2）建立空间直角坐标系，利用空间向量求解线面角；（3）在第二问的基础上求解点面距离.
(1)
取PC的中点M，连接MF，ME，因为F是PB的中点，所以MF是三角形PBC的中点，所以MF∥BC，且，因为底面ABCD为矩形，E是AD的中点，所以AE∥BC，，所以∥，且MF=AE，所以四边形AFME是平行四边形，故AF∥ME，因为平面PCE，平面PCE，所以平面PCE
(2)
因为侧面PAD是正三角形，E是AD的中点，所以，又因为侧面底面ABCD，交线为，所以底面，以E为坐标原点，所在直线为x轴，取BC中点H，EH所在直线为y轴，EP所在直线为z轴建立空间直角坐标系，，，，，，设平面的法向量，则，解得：，令得：，所以，，设直线CF与平面PCE所成角为，故；
所以直线CF与平面PCE所成角的正弦值为.
(3)
点F到平面PCE的距离.
3．如图在直三棱柱中，为的中点，为的中点，是中点，是与的交点，是与的交点.
(1)求证：；
(2)求证：平面；
(3)求直线与平面的距离.
【答案】(1)证明见解析
(2)证明见解析
(3)
【解析】
【分析】
（1）法一：通过建立空间直角坐标系，运用向量数量积证明，法二：通过线面垂直证明，法三:根据三垂线证明；
（2）法一：通过建立空间直角坐标系，运用向量数量积证明，法二：通过面面平行证明线面平行；
（3）法一：通过建立空间直角坐标系，运用向量方法求解，法二：运用等体积法求解.
(1)
证明：法一：在直三棱柱中，因为，以点为坐标原点，
方向分别为轴正方向建立如图所示空间直角坐标系.
因为，所以，
所以
所以，
所以.
法二：连接，在直三棱柱中，有面，
面，所以，又，则，
因为，所以面
因为面，所以
因为，
所以四边形为正方形，所以
因为，所以面
因为面，所以.
法三：用三垂线定理证明：连接，在直三棱柱中，有面
因为面，所以，又，则，
因为，所以面
所以在平面内的射影为，
因为四边形为正方形，所以，
因此根据三垂线定理可知
(2)
证明：法一：因为为的中点，为的中点，为中点，是与的交点，所以､，依题意可知为重心，则，
可得所以，
，设为平面的法向量，
则即取得
则平面的一个法向量为.
所以，则，
因为平面，所以平面.
法二：连接.在正方形中，为的中点，所以且
，所以四边形是平行四边形，所以
又为中点，所以四边形是矩形，所以且
因为且，所以，
所以四边形为平行四边形，
所以.
因为，
平面平面
平面平面，
所以平面平面，
平面，所以平面
(3)
法一：由（2）知平面的一个法向量，且平面，
所以到平面的距离与到平面的距离相等，
，所以，
所以点到平面的距离
所以到平面的距离为
法二：因为分别为和中点，所以为的重心，
所以，所以到平面的距离是到平面距离的.
取中点则，又平面
平面，所以平面，
所以到平面的距离与到平面的距离相等.
设点到平面的距离为，由
得，又，所以，
所以到平面的距离是，
所以到平面的距离为.
4．如图，正方体ABCD­A1B1C1D1的棱长为1， M， N分别是BB1， B1C1的中点．
(1)求直线MN到平面ACD1的距离；
(2)若G是A1B1的中点，求平面MNG与平面ACD1的距离．
【答案】(1)
(2).
【解析】
【分析】
（1）证明MN∥平面ACD1，转化为求点M到平面ACD1的距离，利用向量法求解即可；
（2）证明平面MNG∥平面ACD1，转化为求直线MN到平面ACD1的距离，由（1）得解.
(1)
以分别为轴建立如图所示的空间直角坐标系，
则，
，，，
故.
因为直线MN与AD1不重合，所以MN∥AD1.
又因为MN⊄平面ACD1， AD1⊂平面ACD1，所以MN∥平面ACD1.
故直线MN到平面ACD1的距离等于点M到平面ACD1的距离．
设平面ACD1的一个法向量为，
所以，令，则，所以，
所以点M到平面ACD1的距离为，
即直线MN到平面ACD1的距离为.
(2)
连接A1C1，
因为G， N分别为A1B1， B1C1的中点，所以GN∥A1C1.
又因为A1C1∥AC，所以GN∥AC.
因为GN⊄平面ACD1， AC⊂平面ACD1，所以GN∥平面ACD1.
同理可得MN∥平面ACD1.
因为MN∩GN＝N， MN, GN⊂平面MNG， 所以平面MNG∥平面ACD1，
所以平面MNG与平面ACD1的距离即为直线MN到平面ACD1的距离，由(1)知其为.
练习二 点线、线线距离
5．已知三棱柱的侧棱垂直于底面，，，分别是棱的中点.
(1)求证：平面；
(2)求点到直线的距离.
【答案】(1)证明见解析；
(2).
【解析】
【分析】
(1)以A为坐标原点，建立空间直角坐标系，利用向量证明和即可；
(2)利用向量投影即可求解.
(1)
∵三棱柱的侧棱垂直于底面，，
∴以A为坐标原点，建立如图空间直角坐标系，
∵，分别是棱的中点，
∴，
,
∵，，∴，，
∵,平面,平面，∴平面.
(2)
∵，∴，,
∴，∴，
故点到直线的距离为.
6．已知四棱锥中，底面ABCD是矩形，平面ABCD，，，点M在PD上，且.
(1)求的值；
(2)求点B到直线CM的距离.
【答案】(1)
(2)
【解析】
【分析】
（1）以为原点建立空间直角坐标系，设，通过坐标运算得到结果；
（2）在棱上取点，使得，则长即为所求.
(1)
以为原点建立空间直角坐标系如图所示：
则，0，，，0，，，2，，，2，，
，0，，，2，，，0，，
设，，，则，，，
，
即，，
∴
(2)
在棱上取点，使得，
设，，，
则，又，
∴
故，
因为，
则，
解得，，
∴
∴.
∴点B到直线CM的距离.
7．如图，在四棱锥中，底面ABCD为矩形，底面ABCD，E是AB上一点，.已知，，.
（1）求直线AD与平面PBC间的距离；
（2）求异面直线EC与PB间的距离；
（3）求点B到平面PEC的距离.
【答案】（1）；（2）；（3）
【解析】
【分析】
（1）以为原点，，，分别为，，轴，建立空间直角坐标系，设，，根据得到，再利用向量法求解直线AD与平面PBC间的距离即可.
（2）利用向量法求解异面直线EC与PB间的距离即可.
（3）利用向量法求解求点B到平面PEC的距离即可.
【详解】
（1）由题知：以为原点，，，分别为，，轴，
建立空间直角坐标系，如图所示：
设，，由题知：，，，
，.
因为，所以，解得.
即，，，.
设平面的法向量，
则，令得.
又因为，
所以直线与平面间的距离.
（2）设，满足设，，
因为，，
所以 ，令，得，
又因为，
所以异面直线EC与PB间的距离.
（3）设平面的法向量，，，
所以，令，得，
又因为，
所以点B到平面PEC的距离.
8．如下图，在四棱锥中，已知平面，且四边形为直角梯形，．
（1）求平面与平面所成夹角的余弦值；
（2）求异面直线与之间的距离．
【答案】（1）；（2）．
【解析】
【分析】
以为原点，建立空间直角坐标系，（1）分别求两个平面的法向量，利用二面角的向量公式即得解；（2）设为直线上一点，转化为求点到直线的距离的最小值，即，分析即得解
【详解】
以为原点，所在直线为轴，轴，轴建立如图所示的空间直角坐标系，
则．
（1）因为平面，且平面，
所以，又，且，
所以平面，
所以是平面的一个法向量．
易知，
设平面的法向量为，
则即，
令解得．
所以是平面的一个法向量，
从而，由图得，平面与平面所成夹角为锐角
所以平面与平面所成夹角的余弦值为．
（2），设为直线上一点，
且，因为，
所以，又，
所以点到直线的距离
，
因为，所以，
所以异面直线与之间的距离为．