备战2024年高考数学二轮复习专题06概率的最值问题(原卷版+解析)

这是一份备战2024年高考数学二轮复习专题06概率的最值问题(原卷版+解析)，共38页。试卷主要包含了概率的最值问题等内容，欢迎下载使用。
常见考点
考点一 概率的最值问题
典例1．某种体育比赛采用“五局三胜制”，具体规则为比赛最多进行五场，当参赛的两方有一方先羸得三场比赛，就由该方获胜而比赛结束，每场比赛都需分出胜负.现A，B双方参加比赛，A方在每一场获胜的概率为，假设每场比赛的结果相互独立.
（1）当时，求A方恰在比赛四场后赢得比赛的概率；
（2）若B方在每一场获胜的概率为q，设比赛场数为.
（i）试求的分布列及数学期望；（用P，q表示）
（ⅱ）求的最大值，并给出能够减少比赛场数的建议.
变式1-1．一个口袋中有除颜色外其他均相同的2个白球和个红球（，且），每次从袋中摸出2个球（每次摸球后把这2个球放回袋中），若摸出的2个球颜色相同，则为中奖，否则为不中奖.设一次摸球中奖的概率为.
（1）试用含的代数式表示一次摸球中奖的概率；
（2）若，求三次摸球恰有一次中奖的概率；
（3）记三次摸球恰有一次中奖的概率为，当为何值时，取得最大值？
变式1-2．一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓后要么出现一次音乐，要么不出现音乐，设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．
（1）若一盘游戏中仅出现一次音乐的概率为，求的最大值点；
（2）以（1）中确定的作为p的值，玩3盘游戏，出现音乐的盘数为随机变量X，求每盘游戏出现音乐的概率及随机变量的期望．
变式1-3．2019年女排世界杯（第13届女排世界杯）是由国际排联举办的赛事，比赛于2019年9月14日至9月29日在日本举行，共有12支参赛队伍.本次比赛启用了新的排球用球_，已知这种球的质量指标ξ（单位：）服从正态分布.比赛赛制采取单循环方式，即每支球队进行11场比赛，最后靠积分选出最后冠军.积分规则如下（比赛采取5局3胜制）：比赛中以或取胜的球队积3分，负队积0分；而在比赛中以取胜的球队积2分，负队积1分.9轮过后，积分榜上的前2名分别为中国队和美国队，中国队积26分，美国队积22分.第10轮中国队对抗塞尔维亚队，设每局比赛中国队取胜的概率为.
（1）如果比赛准备了1000个排球，估计质量指标在内的排球个数（计算结果取整数）
（2）第10轮比赛中，记中国队取胜的概率为，求出的最大值点，并以作为p的值，解决下列问题.
（i）在第10轮比赛中，中国队所得积分为X，求X的分布列；
（ii）已知第10轮美国队积3分，判断中国队能否提前一轮夺得冠军（第10轮过后，无论最后一轮即第11轮结果如何，中国队积分最多）？若能，求出相应的概率；若不能，请说明理由.
参考数据：，则，
，.
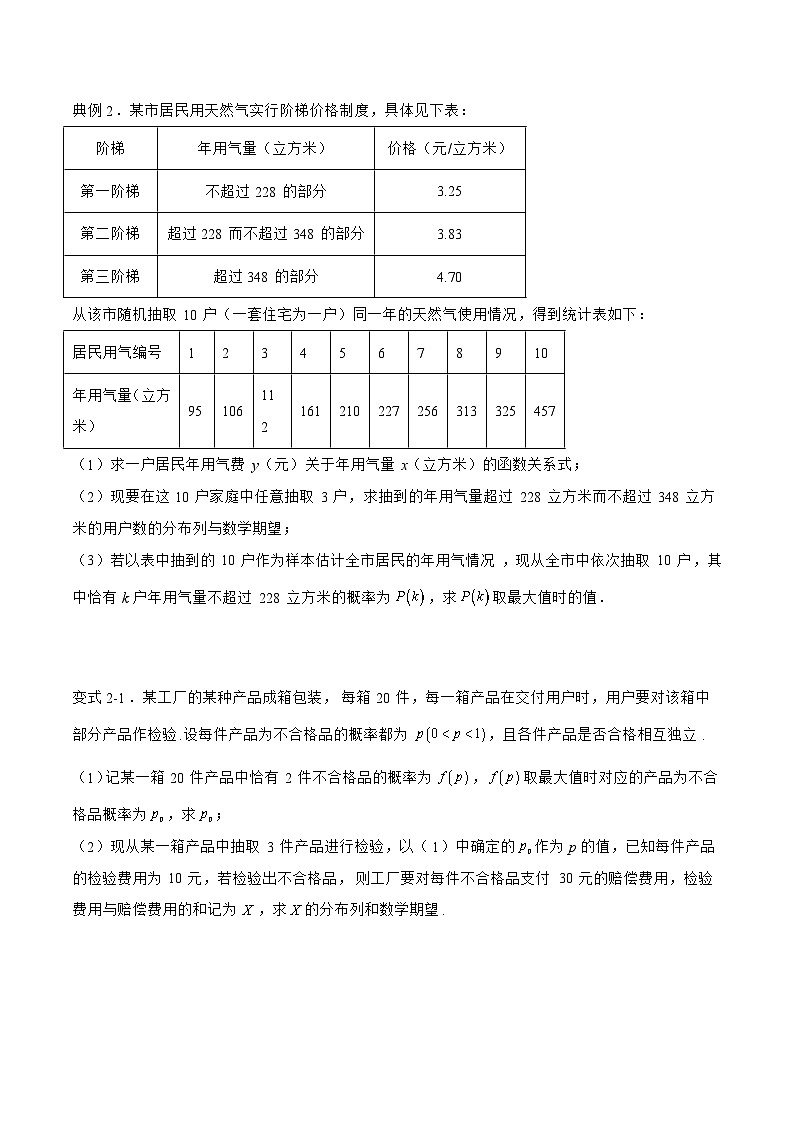
典例2．某市居民用天然气实行阶梯价格制度，具体见下表：
从该市随机抽取10户（一套住宅为一户）同一年的天然气使用情况，得到统计表如下：
（1）求一户居民年用气费y（元）关于年用气量x（立方米）的函数关系式；
（2）现要在这10户家庭中任意抽取3户，求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望；
（3）若以表中抽到的10户作为样本估计全市居民的年用气情况，现从全市中依次抽取10户，其中恰有k户年用气量不超过228立方米的概率为，求取最大值时的值．
变式2-1．某工厂的某种产品成箱包装，每箱20件，每一箱产品在交付用户时，用户要对该箱中部分产品作检验.设每件产品为不合格品的概率都为，且各件产品是否合格相互独立.
（1）记某一箱20件产品中恰有2件不合格品的概率为，取最大值时对应的产品为不合格品概率为，求；
（2）现从某一箱产品中抽取3件产品进行检验，以（1）中确定的作为p的值，已知每件产品的检验费用为10元，若检验出不合格品，则工厂要对每件不合格品支付30元的赔偿费用，检验费用与赔偿费用的和记为，求的分布列和数学期望.
变式2-2．2019年泉州市农村电商发展迅猛，成为创新农产品交易方式、增加农民收入、引导农业供给侧结构性改革、促进乡村振兴的重要力量，成为乡村振兴的新引擎.2019年大学毕业的李想，选择回到家乡泉州自主创业，他在网上开了一家水果网店.2019年双十一期间，为了增加水果销量，李想设计了下面两种促销方案：方案一：购买金额每满120元，即可抽奖一次，中奖可获得20元，每次中奖的概率为（），假设每次抽奖相互独立.方案二：购买金额不低于180元时，即可优惠元，并在优惠后的基础上打九折.
（1）在促销方案一中，设每10个抽奖人次中恰有6人次中奖的概率为，求的最大值点；
（2）若促销方案二中，李想每笔订单得到的金额均不低于促销前总价的八折，求的最大值；
（3）以（1）中确定的作为的值，且当取最大值时，若某位顾客一次性购买了360元，则该顾客应选择哪种促销方案？请说明理由.
变式2-3某省年开始将全面实施新高考方案．在门选择性考试科目中，物理、历史这两门科目采用原始分计分；思想政治、地理、化学、生物这4门科目采用等级转换赋分，将每科考生的原始分从高到低划分为，，，，共个等级，各等级人数所占比例分别为、、、和，并按给定的公式进行转换赋分．该省组织了一次高一年级统一考试，并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分．
（1）某校生物学科获得等级的共有10名学生，其原始分及转换分如下表：
现从这10名学生中随机抽取3人，设这3人中生物转换分不低于分的人数为，求的分布列和数学期望；
（2）假设该省此次高一学生生物学科原始分服从正态分布．若，令，则，请解决下列问题：
①若以此次高一学生生物学科原始分等级的最低分为实施分层教学的划线分，试估计该划线分大约为多少分？（结果保留为整数）
②现随机抽取了该省名高一学生的此次生物学科的原始分，若这些学生的原始分相互独立，记为被抽到的原始分不低于分的学生人数，求取得最大值时的值．
附：若，则，．
巩固练习
练习一 概率的最值问题
1．某次围棋比赛的决赛，由甲乙两人争夺最后的冠军，决赛先进行两天，每天实行三盘两胜制，即先赢两盘者获得该天胜利，此时该天比赛结束．若甲乙中的一方能连续两天胜利，则其为最终冠军；若前两天双方各赢一天，则第三天只进行一盘附加赛，该附加赛的获胜方为最终冠军．设每盘比赛甲获胜的概率为，每盘比赛的结果没有平局且结果互相独立．
(1)记第一天需要进行的比赛盘数为X．
（ⅰ）求，并求当取最大值时p的值；
（ⅱ）结合实际，谈谈（ⅰ）中结论的意义；
(2)当时，记总共进行的比赛盘数为Y，求．
2．在新冠肺炎疫情肆虐之初，作为重要防控物资之一的口罩是医务人员和人民群众抗击疫情的武器与保障，为了打赢疫情防控阻击战，我国企业依靠自身强大的科研能力，果断转产自行研制新型全自动高速口罩生产机，“争分夺秒､保质保量”成为口罩生产线上的重要标语
(1)在试产初期，某新型全自动高速口罩生产流水线有四道工序，前三道工序完成成品口罩的生产且互不影响，第四道是检测工序.已知批次A的成品口罩生产中，前三道工序的次品率分别为，，.求批次A成品口罩的次品率.
(2)已知某批次成品口罩的次品率为，设100个成品口罩中恰有1个不合格品的概率为，记的最大值点为，改进生产线后批次的口罩的次品率.某医院获得批次，的口罩捐赠并分发给该院医务人员使用.经统计，正常佩戴使用这两个批次的口罩期间，该院医务人员核酸检测情况如条形图所示；求出，并判断是否有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关？
3．为考察本科生基本学术规范和基本学术素养，某大学决定对各学院本科毕业论文进行抽检，初步方案是本科毕业论文抽检每年进行一次，抽检对象为上一学年度授予学士学位的论文，初评阶段，每篇论文送位同行专家进行评审，位专家中有位以上（含位）专家评议意见为“不合格”的毕业论文，将认定为“存在问题毕业论文”.位专家中有位专家评议意见为“不合格”，将再送位同行专家（不同于前位）进行复评.复评阶段，位复评专家中有位以上（含位）专家评议意见为“不合格”，将认定为“存在问题毕业论文”.每位专家，判定每篇论文“不合格”的概率均为，且各篇毕业论文是否被判定为“不合格”相互独立.
(1)若，求每篇毕业论文被认定为“存在问题毕业论文”的概率是多少；
(2)学校拟定每篇论文需要复评的评审费用为元，不需要复评的评审费用为元，则每篇论文平均评审费用的最大值是多少？
4．某地区出现了一种病毒性传染病疫情，该病毒是一种人传人，不易被人们直接发现，潜伏时间长，传染性极强的病毒.我们把与该病毒感染者有过密切接触的人群称为密切接触者，一旦发现感染者，社区会立即对其进行流行病学调查，找到其密切接触者进行隔离观察.通过病毒指标检测，每位密切接触者为阳性的概率为，且每位密切接触者病毒指标是否为阳性相互独立.调查发现某位感染者共有10位密切接触者，将这10位密切接触者隔离之后立即进行病毒指标检测.检测方式既可以采用逐个检测，又可以采用“合1检测法”.“合1检测法”是将个样本混合在一起检测，混合样本中只要发现阳性，则该组中各个样本必须再逐个检测；若混合样本为阴性，则可认为该混合样本中每个人都是阴性.
(1)若逐个检测，发现恰有2个人样本检测结果为阳性的概率为，求的最大值点；
(2)若采用“ 5合1检测法”，总检测次数为，求随机变量的分布列及数学期望；
(3)若采用“10合1检测法”，总检测次数的数学期望为，以（1）中确定的作为的值，试比较与的大小(精确到0.1).
附：.
5．学习强国中有两项竞赛答题活动，一项为“双人对战”，另一项为“四人赛”．活动规则如下：一天内参与“双人对战”活动，仅首局比赛可获得积分，获胜得2分，失败得1分；一天内参与“四人赛”活动，仅前两局比赛可获得积分，首局获胜得3分，次局获胜得2分，失败均得1分．已知李明参加“双人对战”活动时，每局比赛获胜的概率为；参加“四人赛”活动（每天两局）时，第一局和第二局比赛获胜的概率分别为p，．李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动（每天两局），各局比赛互不影响．
(1)求李明这5天参加“双人对战”活动的总得分X的分布列和数学期望；
(2)设李明在这5天的“四人赛”活动（每天两局）中，恰有3天每天得分不低于3分的概率为．求p为何值时，取得最大值．
6．某校开展“学习新中国史”的主题学习活动.为了调查学生对新中国史的了解情况，需要对学生进行答题测试，答题测试的规则如下：每位参与测试的学生最多有两次答题机会，每次答一题，第一次答对，答题测试过关，得5分，停止答题测试；第一次答错，继续第二次答题，若答对，答题测试过关，得3分；若两次均答错，答题测试不过关，得0分.某班有12位学生参与答题测试，假设每位学生第一次和第二次答题答对的概率分别为m，0.5，两次答题是否答对互不影响，每位学生答题测试过关的概率为P.
(1)若，求每一位参与答题测试的学生所得分数的数学期望；
(2)设该班恰有9人答题测试过关的概率为，当取最大值时，求，m.
7．为落实立德树人根本任务，坚持五育并举全面推进素质教育，某学校举行了乒乓球比赛，其中参加男子乒乓球决赛的12名队员来自3个不同校区，三个校区的队员人数分别是3，4，5.本次决赛的比赛赛制采取单循环方式，即每名队员进行11场比赛（每场比赛都采取5局3胜制），最后根据积分选出最后的冠军.积分规则如下：比赛中以或取胜的队员积3分，失败的队员积0分；而在比赛中以取胜的队员积2分，失败的队员的队员积1分.已知第10轮张三对抗李四，设每局比赛张三取胜的概率均为.
（1）比赛结束后冠亚军恰好来自不同校区的概率是多少？
（2）第10轮比赛中，记张三取胜的概率为.
①求出的最大值点；
②若以作为的值，这轮比赛张三所得积分为，求的分布列及期望.
8．通过历次考试，微信公众号小艺学堂，学生容易在多选题中由于多选和错选致误，因此决定为自己所带的两个班级的学生命制一套满分为100分的多项选择题专题卷，已知这两个班共有学生100名，陈老师根据两个班学生的考试成绩制作了如下表所示的频率分布表：
（Ⅰ）若每个分组取中间值作代表，试求两个班学生的成绩的平均值；
（Ⅱ）为了更好地激发学生学习政治的热情，陈老师决定组建政治兴趣小组，若采取分层抽样的方法从两个班中成绩为和的学生中抽取5人，再从中确定3人为小组组长，如果用表示小组组长来自成绩为的学生的人数，求的分布列和数学期望；
（Ⅲ）为了更好地了解学生多项选择题失分的原因，陈老师从两个班中随机抽取20名学生进行深入交流，若这20名学生中有名学生本次考试成绩在之间的概率为（，），求取得最大值时的值（将频率视为概率）.
阶梯
年用气量（立方米）
价格（元/立方米）
第一阶梯
不超过228的部分
3.25
第二阶梯
超过228而不超过348的部分
3.83
第三阶梯
超过348的部分
4.70
居民用气编号
1
2
3
4
5
6
7
8
9
10
年用气量（立方米）
95
106
112
161
210
227
256
313
325
457
原始分
91
90
89
88
87
85
83
82
转换分
100
99
97
95
94
91
88
86
人数
1
1
2
1
2
1
1
1
分值
频率
第四篇 概率与统计
专题06 概率的最值问题
常见考点
考点一 概率的最值问题
典例1．某种体育比赛采用“五局三胜制”，具体规则为比赛最多进行五场，当参赛的两方有一方先羸得三场比赛，就由该方获胜而比赛结束，每场比赛都需分出胜负.现A，B双方参加比赛，A方在每一场获胜的概率为，假设每场比赛的结果相互独立.
（1）当时，求A方恰在比赛四场后赢得比赛的概率；
（2）若B方在每一场获胜的概率为q，设比赛场数为.
（i）试求的分布列及数学期望；（用P，q表示）
（ⅱ）求的最大值，并给出能够减少比赛场数的建议.
【答案】（1）；（2）（i）分布列见解析，；（ⅱ），建议A，B双方扩大与对方每一场获胜的概率，可减少比赛场数.
【解析】
【分析】
（1）根据A方在前三场中有两场获胜，且第四场获胜，可得结果；
（2）（i）取值为3，4，5.求出取各个值的概率即可得分布列；
（ⅱ）根据和可得结果，
【详解】
（1）A方恰在比赛四场后赢得比赛，则A方在前三场中有两场获胜，且第四场获胜，
所以A方恰在比赛四场后赢得比赛的概率为；建议A，B双方扩大与对方每一场获胜的概率，可减少比赛场数.
（2）（i）易知，取值为3，4，5.
，
，
，
故的概率分布列为：
所以点的数学期望为
.
.
（ⅱ），
因为，，所以，所以在，
即时，取得最大值，最大值为.
由数学期望的表达式可知当时，单调递增，
所以接近0时，即当p，q相差较大时，也就是，或者，时，
比赛场数的数学期望相对较小，
故建议A，B双方扩大与对方每一场获胜的概率，可减少比赛场数.
【点睛】
本题考查了独立重复试验的概率公式，考查了离散型随机变量的分布列，考查了离散型随机变量的数学期望，属于中档题.
变式1-1．一个口袋中有除颜色外其他均相同的2个白球和个红球（，且），每次从袋中摸出2个球（每次摸球后把这2个球放回袋中），若摸出的2个球颜色相同，则为中奖，否则为不中奖.设一次摸球中奖的概率为.
（1）试用含的代数式表示一次摸球中奖的概率；
（2）若，求三次摸球恰有一次中奖的概率；
（3）记三次摸球恰有一次中奖的概率为，当为何值时，取得最大值？
【答案】（1）；（2）；（3）.
【解析】
【分析】
（1）求出从个球中任选2个的情况，再求出任选的2个球颜色相同的情况即可得出；
（2）根据独立重复试验的特点可直接求出；
（3）根据题意表示出，利用导数可求解.
【详解】
（1）从个球中任选2个，有种选法，任选的2个球颜色相同，有种选法，
∴一次摸球中奖的概率.
（2）若，则一次摸球中奖的概率为.
三次摸球是独立重复试验，则三次摸球中恰有一次中奖的概率是.
（3）由题意，得三次摸球恰有一次中奖的概率是，.
，
∴在上单调递增，在上单调递减，
∴当时，取得最大值，
由（1）知（，且），
得，即时，取得最大值.
变式1-2．一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓后要么出现一次音乐，要么不出现音乐，设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．
（1）若一盘游戏中仅出现一次音乐的概率为，求的最大值点；
（2）以（1）中确定的作为p的值，玩3盘游戏，出现音乐的盘数为随机变量X，求每盘游戏出现音乐的概率及随机变量的期望．
【答案】（1）；（2）；.
【解析】
【分析】
（1）根据独立性重复实验的概率公式计算出，然后根据函数性质即可求出最大值点；
（2）先算每盘不出现音乐的概率，即可算出每盘游戏出现音乐的概率，可知随机变量X服从二项分布，直接根据公式可计算期望.
【详解】
（1）由题可知，一盘游戏中仅出现一次音乐的概率为：
，
，
由得或（舍），
当时，；
当时，，
∴在上单调递增，在上单调递减，
∴当时，有最大值，即的最大值点．
（2）由（1）知，，
则每盘游戏出现音乐的概率为．
由题可知，
∴．
【点睛】
本题考查独立性重复实验的概率，以及二项分布的均值的计算.
变式1-3．2019年女排世界杯（第13届女排世界杯）是由国际排联举办的赛事，比赛于2019年9月14日至9月29日在日本举行，共有12支参赛队伍.本次比赛启用了新的排球用球_，已知这种球的质量指标ξ（单位：）服从正态分布.比赛赛制采取单循环方式，即每支球队进行11场比赛，最后靠积分选出最后冠军.积分规则如下（比赛采取5局3胜制）：比赛中以或取胜的球队积3分，负队积0分；而在比赛中以取胜的球队积2分，负队积1分.9轮过后，积分榜上的前2名分别为中国队和美国队，中国队积26分，美国队积22分.第10轮中国队对抗塞尔维亚队，设每局比赛中国队取胜的概率为.
（1）如果比赛准备了1000个排球，估计质量指标在内的排球个数（计算结果取整数）
（2）第10轮比赛中，记中国队取胜的概率为，求出的最大值点，并以作为p的值，解决下列问题.
（i）在第10轮比赛中，中国队所得积分为X，求X的分布列；
（ii）已知第10轮美国队积3分，判断中国队能否提前一轮夺得冠军（第10轮过后，无论最后一轮即第11轮结果如何，中国队积分最多）？若能，求出相应的概率；若不能，请说明理由.
参考数据：，则，
，.
【答案】（1）477个；（2）；（i）见解析；（ii）能提前一轮夺得冠军，.
【解析】
【分析】
（1）由正态分布原则即可求出排球个数；
（2）根据二项分布先求出，再利用导数求出取最大值时的值；根据比赛积分规则，得出中国队得分可能的取值，然后求出其分布列；由的分布列分析即可得出能否提前一轮夺得冠军并求得其概率.
【详解】
解：∵，∴
所以质量指标在内的排球个数约为个
（2），.
令，得.
当时，，在上为增函数；
当时，，在上为减函数.
所以的最大值点.从而.
的可能取值为.
，
，
，
，
的分布列为
若，则中国队10轮后的总积分为29分，美国队即便第10轮和第11轮都积3分，则11轮过后的总积分是28分，，所以，中国队如果第10轮积3分，则可提前一轮夺得冠军，其概率为.
【点睛】
本题考查正态分布、二项分布、离散型随机变量的分布列及导数的应用，知识点交叉渗透，综合性强，属于中档题.
典例2．某市居民用天然气实行阶梯价格制度，具体见下表：
从该市随机抽取10户（一套住宅为一户）同一年的天然气使用情况，得到统计表如下：
（1）求一户居民年用气费y（元）关于年用气量x（立方米）的函数关系式；
（2）现要在这10户家庭中任意抽取3户，求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望；
（3）若以表中抽到的10户作为样本估计全市居民的年用气情况，现从全市中依次抽取10户，其中恰有k户年用气量不超过228立方米的概率为，求取最大值时的值．
【答案】（1）；（2）分布列见解析，数学期望为；（3）6．
【解析】
【分析】
（1）由表格中的数据结合题意，即可求得一户居民年用气费y（元）关于年用气量x（立方米）的函数关系式；
（2）由题意知10户家庭中年用气量超过228立方米而不超过348立方米的用户有3户，得到随机变量可取，利用超几何分布求得相应的概率，得到随机变量的分布列，进而求得期望；
（3）由，列出不等式组由，求得的值，即可求解.
【详解】
（1）由题意，当时，；
当时，；
当时，，
所以年用气费y关于年用气量x的函数关系式为.
（2）由题知10户家庭中年用气量超过228立方米而不超过348立方米的用户有3户，
设取到年用气量超过228立方米而不超过348立方米的用户数为，则可取，
则，，
，，
故随机变量的分布列为：
所以.
（3）由题意知，
由，解得，，
所以当时，概率最大，所以.
【点睛】
本题主要考查了分段函数模型的性质及其应用，以及离散型随机变量的分布列与期望的求解，着重考查了分析问题和解答问题的能力，属于中档试题.
变式2-1．某工厂的某种产品成箱包装，每箱20件，每一箱产品在交付用户时，用户要对该箱中部分产品作检验.设每件产品为不合格品的概率都为，且各件产品是否合格相互独立.
（1）记某一箱20件产品中恰有2件不合格品的概率为，取最大值时对应的产品为不合格品概率为，求；
（2）现从某一箱产品中抽取3件产品进行检验，以（1）中确定的作为p的值，已知每件产品的检验费用为10元，若检验出不合格品，则工厂要对每件不合格品支付30元的赔偿费用，检验费用与赔偿费用的和记为，求的分布列和数学期望.
【答案】（1）；（2）分布列见解析；.
【解析】
【分析】
（1）根据二项分布概率公式可得，利用导数可确定单调性，从而得到最大值点；
（2）首先确定所有可能的取值和对应的概率，由此得到分布列；根据数学期望计算公式计算可得期望.
【详解】
（1）件产品中恰有件不合格品的概率，
，
令，又，解得：，
当时，；当时，；
在上单调递增，在上单调递减，
当时，取得最大值，即.
（2）由题意得：所有可能的取值为：，，，，
；；
；；
的分布列为：
数学期望.
【点睛】
本题考查二项分布概率问题的求解以及服从于二项分布的随机变量的分布列与数学期望的求解问题；解题关键是能够利用导数的知识确定关于概率的函数的单调性，进而确定最值点.
变式2-2．2019年泉州市农村电商发展迅猛，成为创新农产品交易方式、增加农民收入、引导农业供给侧结构性改革、促进乡村振兴的重要力量，成为乡村振兴的新引擎.2019年大学毕业的李想，选择回到家乡泉州自主创业，他在网上开了一家水果网店.2019年双十一期间，为了增加水果销量，李想设计了下面两种促销方案：方案一：购买金额每满120元，即可抽奖一次，中奖可获得20元，每次中奖的概率为（），假设每次抽奖相互独立.方案二：购买金额不低于180元时，即可优惠元，并在优惠后的基础上打九折.
（1）在促销方案一中，设每10个抽奖人次中恰有6人次中奖的概率为，求的最大值点；
（2）若促销方案二中，李想每笔订单得到的金额均不低于促销前总价的八折，求的最大值；
（3）以（1）中确定的作为的值，且当取最大值时，若某位顾客一次性购买了360元，则该顾客应选择哪种促销方案？请说明理由.
【答案】（1）；（2）20元；（3）选择方案一，理由见解析
【解析】
【分析】
(1) 依题意得：，利用求导，即可求出最值
(2) 设顾客一次购买水果的促销前总价为，当元时，有恒成立，利用参变分离法，把和分别放在不等式两边即可求解.
(3)分别列出参加两种活动的方案，然后分别计算出减负金额即可判断应选择哪种促销方案
【详解】
解：（1）依题意得：，
则，
当时，；当时，，
故在时取得最大值，所以.
（2）设顾客一次购买水果的促销前总价为，
当元时，有恒成立，
即恒成立，所以，故的最大值为20元.
（3）若参加活动一，顾客可抽奖三次.设X表示顾客在三次抽奖中中奖的次数，
由于顾客每次抽奖的结果相互独立，则，
所以.
由于顾客每中一次可获得20元现金奖励，
因此该顾客在三次抽奖中可获得的奖励金额的均值为元，
若参加活动二，顾客可得减负金额为元.
又因为，所以顾客应该选择活动二.
【点睛】
本题考查利用导数求最值，参变分离法，以及二项分布的数学期望问题，属于基础题.
变式2-3某省年开始将全面实施新高考方案．在门选择性考试科目中，物理、历史这两门科目采用原始分计分；思想政治、地理、化学、生物这4门科目采用等级转换赋分，将每科考生的原始分从高到低划分为，，，，共个等级，各等级人数所占比例分别为、、、和，并按给定的公式进行转换赋分．该省组织了一次高一年级统一考试，并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分．
（1）某校生物学科获得等级的共有10名学生，其原始分及转换分如下表：
现从这10名学生中随机抽取3人，设这3人中生物转换分不低于分的人数为，求的分布列和数学期望；
（2）假设该省此次高一学生生物学科原始分服从正态分布．若，令，则，请解决下列问题：
①若以此次高一学生生物学科原始分等级的最低分为实施分层教学的划线分，试估计该划线分大约为多少分？（结果保留为整数）
②现随机抽取了该省名高一学生的此次生物学科的原始分，若这些学生的原始分相互独立，记为被抽到的原始分不低于分的学生人数，求取得最大值时的值．
附：若，则，．
【答案】（1）分布列详见解析，数学期望为；（2）①69分；②．
【解析】
【分析】
（1）写出随机变量的所有可能的取值，根据超几何分布求出的每个值对应的概率，列出分布列，求出数学期望；
（2）①设该划线分为，由求出.由，得.由题意，又，故，故，即可求出；②由题意，根据独立重复实验的概率计算公式，求出，代入不等式组，即求的值.
【详解】
（1）随机变量的所有可能的取值为.
由题意可得：，，
，，
随机变量的分布列为
数学期望．
（2）①设该划线分为，由得，
令，则，
由题意，，即，
，，，
，，取．
②由①讨论及参考数据得
，
即每个学生生物统考成绩不低于分的事件概率约为，
，．
由
即
解得，
，，
当时，取得最大值．
【点睛】
本题考查超几何分布、二项分布及正态分布，考查学生的数据处理能力和运算求解能力，属于较难的题目．
巩固练习
练习一 概率的最值问题
1．某次围棋比赛的决赛，由甲乙两人争夺最后的冠军，决赛先进行两天，每天实行三盘两胜制，即先赢两盘者获得该天胜利，此时该天比赛结束．若甲乙中的一方能连续两天胜利，则其为最终冠军；若前两天双方各赢一天，则第三天只进行一盘附加赛，该附加赛的获胜方为最终冠军．设每盘比赛甲获胜的概率为，每盘比赛的结果没有平局且结果互相独立．
(1)记第一天需要进行的比赛盘数为X．
（ⅰ）求，并求当取最大值时p的值；
（ⅱ）结合实际，谈谈（ⅰ）中结论的意义；
(2)当时，记总共进行的比赛盘数为Y，求．
【答案】(1)（i），取最大值时，（ii）结合实际，当时双方实力最接近，比赛越激烈，则一天中进行比赛的盘数会更多
(2)
【解析】
【分析】
（1）X可能取值为2，3，分别求解对应的概率，根据期望的定义求解，再根据二次函数的性质求最值即可；
（2）即或，即获胜方两天均为获胜或者获胜方前两天的比分为和或者和再加附加赛，分别计算概率即可
(1)
（i）X可能取值为2，3，
；
故
即，则当时，取得最大值.
（ii）结合实际，当时双方实力最接近，比赛越激烈，则一天中进行比赛的盘数会更多．
(2)
当时，双方前两天的比分为或的概率均为
比分为或的概率均为
则或，
即获胜方两天均为获胜，
故；
即获胜方前两天的比分为和或者和再加附加赛，
故
所以
2．在新冠肺炎疫情肆虐之初，作为重要防控物资之一的口罩是医务人员和人民群众抗击疫情的武器与保障，为了打赢疫情防控阻击战，我国企业依靠自身强大的科研能力，果断转产自行研制新型全自动高速口罩生产机，“争分夺秒､保质保量”成为口罩生产线上的重要标语
(1)在试产初期，某新型全自动高速口罩生产流水线有四道工序，前三道工序完成成品口罩的生产且互不影响，第四道是检测工序.已知批次A的成品口罩生产中，前三道工序的次品率分别为，，.求批次A成品口罩的次品率.
(2)已知某批次成品口罩的次品率为，设100个成品口罩中恰有1个不合格品的概率为，记的最大值点为，改进生产线后批次的口罩的次品率.某医院获得批次，的口罩捐赠并分发给该院医务人员使用.经统计，正常佩戴使用这两个批次的口罩期间，该院医务人员核酸检测情况如条形图所示；求出，并判断是否有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关？
【答案】(1)
(2)，有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关.
【解析】
【分析】
（1）根据对立事件的概率的求法，可得批次成品口罩的次品率为，代入数据计算即可；
(2) 由题意可得，求出导数，得出函数的单调区间，从得出的值.再列出列联表，再由公式求出，再与临界值比较，得出结论.
(1)
批次成品口罩的次品率为；
(2)
100个成品口罩中恰有1个不合格的概率为，
所以，
令，解得，
当时，，当时，，
所以在上单调递增，在上单调递减.
所以的最大值点为，
由条形图可建立列联表如下：
则，
因此，有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关.
3．为考察本科生基本学术规范和基本学术素养，某大学决定对各学院本科毕业论文进行抽检，初步方案是本科毕业论文抽检每年进行一次，抽检对象为上一学年度授予学士学位的论文，初评阶段，每篇论文送位同行专家进行评审，位专家中有位以上（含位）专家评议意见为“不合格”的毕业论文，将认定为“存在问题毕业论文”.位专家中有位专家评议意见为“不合格”，将再送位同行专家（不同于前位）进行复评.复评阶段，位复评专家中有位以上（含位）专家评议意见为“不合格”，将认定为“存在问题毕业论文”.每位专家，判定每篇论文“不合格”的概率均为，且各篇毕业论文是否被判定为“不合格”相互独立.
(1)若，求每篇毕业论文被认定为“存在问题毕业论文”的概率是多少；
(2)学校拟定每篇论文需要复评的评审费用为元，不需要复评的评审费用为元，则每篇论文平均评审费用的最大值是多少？
【答案】(1)；
(2)元.
【解析】
【分析】
（1）根据二项分布和独立事件概率公式可表示出所求概率，代入即可得到结果；
（2）分别求得评审费用所有可能取值对应的概率，可得，利用导数可求得的最大值，由此可确定结果.
(1)
设每篇毕业论文被认定为“存在问题毕业论文”为事件，
则，
，；
(2)
设每篇文章的评审费用为元，则的可能取值为，，
则，；
.
令，，则.
当时，，在上单调递增，
当时，，在上单调递减，
的最大值为，每篇论文平均评审费用的最大值是元.
4．某地区出现了一种病毒性传染病疫情，该病毒是一种人传人，不易被人们直接发现，潜伏时间长，传染性极强的病毒.我们把与该病毒感染者有过密切接触的人群称为密切接触者，一旦发现感染者，社区会立即对其进行流行病学调查，找到其密切接触者进行隔离观察.通过病毒指标检测，每位密切接触者为阳性的概率为，且每位密切接触者病毒指标是否为阳性相互独立.调查发现某位感染者共有10位密切接触者，将这10位密切接触者隔离之后立即进行病毒指标检测.检测方式既可以采用逐个检测，又可以采用“合1检测法”.“合1检测法”是将个样本混合在一起检测，混合样本中只要发现阳性，则该组中各个样本必须再逐个检测；若混合样本为阴性，则可认为该混合样本中每个人都是阴性.
(1)若逐个检测，发现恰有2个人样本检测结果为阳性的概率为，求的最大值点；
(2)若采用“ 5合1检测法”，总检测次数为，求随机变量的分布列及数学期望；
(3)若采用“10合1检测法”，总检测次数的数学期望为，以（1）中确定的作为的值，试比较与的大小(精确到0.1).
附：.
【答案】(1)
(2)分布列见解析，
(3)
【解析】
【分析】
（1）根据独立事件的乘法公式结合导数得出的最大值点；
（2）总检测次数为可能为，求出相应概率，列出分布列计算数学期望；
（3）先计算出与，再比较大小.
(1)
有2个人样本检测结果为阳性的概率为
令，得，当时，；当时，
即函数在上为单调递增，在上单调递减，即的最大值点
(2)
采用“5合1检测法”，总检测次数为可能为
随机变量的分布列为
数学期望为
(3)
当时，
采用“10合1检测法”，总检测次数可能是
数学期望
【点睛】
方法点睛：求离散型随机变量的分布列以及期望的步骤：
（1）理解随机变量的意义，写出的所有可能取值
（2）求取每个值的概率
（3）写出的分布列
（4）由均值的定义求
5．学习强国中有两项竞赛答题活动，一项为“双人对战”，另一项为“四人赛”．活动规则如下：一天内参与“双人对战”活动，仅首局比赛可获得积分，获胜得2分，失败得1分；一天内参与“四人赛”活动，仅前两局比赛可获得积分，首局获胜得3分，次局获胜得2分，失败均得1分．已知李明参加“双人对战”活动时，每局比赛获胜的概率为；参加“四人赛”活动（每天两局）时，第一局和第二局比赛获胜的概率分别为p，．李明周一到周五每天都参加了“双人对战”活动和“四人赛”活动（每天两局），各局比赛互不影响．
(1)求李明这5天参加“双人对战”活动的总得分X的分布列和数学期望；
(2)设李明在这5天的“四人赛”活动（每天两局）中，恰有3天每天得分不低于3分的概率为．求p为何值时，取得最大值．
【答案】(1)分布列见解析，（分）
(2)
【解析】
【分析】
（1）可取5，6，7，8，9，10，求出对应随机变量的概率，从而可求出分布列，再根据期望公式求出数学期望即可；
（2）先求出一天得分不低于3分的概率，再求出恰有3天每天得分不低于3分的概率为，再根据导出求出函数的单调区间，即可得出答案.
(1)
解：可取5，6，7，8，9，10，
，，
，，
，，
分布列如下：
所以（分）；
(2)
解：设一天得分不低于3分为事件，
则，
则恰有3天每天得分不低于3分的概率，
则
，
当时，，当时，，
所以函数在上递增，在上递减，
所以当时，取得最大值.
6．某校开展“学习新中国史”的主题学习活动.为了调查学生对新中国史的了解情况，需要对学生进行答题测试，答题测试的规则如下：每位参与测试的学生最多有两次答题机会，每次答一题，第一次答对，答题测试过关，得5分，停止答题测试；第一次答错，继续第二次答题，若答对，答题测试过关，得3分；若两次均答错，答题测试不过关，得0分.某班有12位学生参与答题测试，假设每位学生第一次和第二次答题答对的概率分别为m，0.5，两次答题是否答对互不影响，每位学生答题测试过关的概率为P.
(1)若，求每一位参与答题测试的学生所得分数的数学期望；
(2)设该班恰有9人答题测试过关的概率为，当取最大值时，求，m.
【答案】(1)
(2)，
【解析】
【分析】
（1）设每一位参与答题测试的学生所得分数为，求出对应概率，进而得出数学期望；
（2）该班恰有9人答题测试过关的概率为，再由导数得出其单调性，进而得出取得最大值时，m的值.
(1)
设每一位参与答题测试的学生所得分数为，则可取
即每一位参与答题测试的学生所得分数的数学期望为
(2)
根据题意，该班恰有9人答题测试过关的概率为
，
故在上单调递增，在上单调递减
故当时，取最大值，此时
7．为落实立德树人根本任务，坚持五育并举全面推进素质教育，某学校举行了乒乓球比赛，其中参加男子乒乓球决赛的12名队员来自3个不同校区，三个校区的队员人数分别是3，4，5.本次决赛的比赛赛制采取单循环方式，即每名队员进行11场比赛（每场比赛都采取5局3胜制），最后根据积分选出最后的冠军.积分规则如下：比赛中以或取胜的队员积3分，失败的队员积0分；而在比赛中以取胜的队员积2分，失败的队员的队员积1分.已知第10轮张三对抗李四，设每局比赛张三取胜的概率均为.
（1）比赛结束后冠亚军恰好来自不同校区的概率是多少？
（2）第10轮比赛中，记张三取胜的概率为.
①求出的最大值点；
②若以作为的值，这轮比赛张三所得积分为，求的分布列及期望.
【答案】（1）；（2）①；②分布列答案见解析，数学期望：.
【解析】
【分析】
（1）利用互斥事件的概率公式即得；
（2）由题可求，然后利用导数可求最值，再利用条件可求随机变量的分布列，即得.
【详解】
（1）比赛结束后冠亚军恰好来自不同校区的概率是；
（2）①由题可知，
，
令，得，
当时，，在上单调递增；
当时，，在上单调递减.
所以的最大值点，
②的可能取值为0，1，2，3.
；
；
；.
所以的分布列为
的期望为.
8．通过历次考试，微信公众号小艺学堂，学生容易在多选题中由于多选和错选致误，因此决定为自己所带的两个班级的学生命制一套满分为100分的多项选择题专题卷，已知这两个班共有学生100名，陈老师根据两个班学生的考试成绩制作了如下表所示的频率分布表：
（Ⅰ）若每个分组取中间值作代表，试求两个班学生的成绩的平均值；
（Ⅱ）为了更好地激发学生学习政治的热情，陈老师决定组建政治兴趣小组，若采取分层抽样的方法从两个班中成绩为和的学生中抽取5人，再从中确定3人为小组组长，如果用表示小组组长来自成绩为的学生的人数，求的分布列和数学期望；
（Ⅲ）为了更好地了解学生多项选择题失分的原因，陈老师从两个班中随机抽取20名学生进行深入交流，若这20名学生中有名学生本次考试成绩在之间的概率为（，），求取得最大值时的值（将频率视为概率）.
【答案】（Ⅰ）54；（Ⅱ）分布列见解析，；（Ⅲ）8.
【解析】
【分析】
（Ⅰ）每个分组取中间值与频率相乘后求和可得平均值；
（Ⅱ）由频率分布表可知，若采取分层抽样的方法可知的可能取值为1，2，3，求出对应概率可得分布列，利用期望公式可得结果；
（Ⅲ）设在抽取的20名学生中，成绩在的人数为，则，故，利用单调性可得结果.
【详解】
（Ⅰ）两个班学生的成绩的平均值为.
（Ⅱ）由频率分布表可知，若采取分层抽样的方法从两个班中成绩为和的学生中抽取5人，则应从成绩为和的学生中各抽取3人和2人，所以的可能取值为1，2，3.
，，，
所以的分布列为
所以的数学期望为.
（Ⅲ）设在抽取的20名学生中，成绩在的人数为，则，
所以.
设.
当时，，，当时，，.
所以当时，最大.
【点睛】
本题主要考查平均值的求解，独立重复试验的概率公式以及离散型随机变量的分布列与数学期望，属于中档题. 求解数学期望问题，首先要正确理解题意，其次要准确无误的找出随机变量的所有可能值，计算出相应的概率，写出随机变量的分布列，正确运用均值、方差的公式进行计算，也就是要过三关：（1）阅读理解关；（2）概率计算关；（3）公式应用关.
3
4
5
P
3
2
1
0
阶梯
年用气量（立方米）
价格（元/立方米）
第一阶梯
不超过228的部分
3.25
第二阶梯
超过228而不超过348的部分
3.83
第三阶梯
超过348的部分
4.70
居民用气编号
1
2
3
4
5
6
7
8
9
10
年用气量（立方米）
95
106
112
161
210
227
256
313
325
457
0
1
2
3
P
原始分
91
90
89
88
87
85
83
82
转换分
100
99
97
95
94
91
88
86
人数
1
1
2
1
2
1
1
1
核酸检测结果
口罩批次
合计
呈阳性
12
3
15
呈阴性
28
57
85
合计
40
60
100
5
6
7
8
9
10
0
1
2
3
分值
频率
1
2
3