

所属成套资源:2024年高考数学二轮复习专题(考法分类新高考版)(原卷版+解析)
2024年高考数学二轮复习专题04恒成立与存在性求参(选填题6种考法)(原卷版+解析)
展开
这是一份2024年高考数学二轮复习专题04恒成立与存在性求参(选填题6种考法)(原卷版+解析),共52页。试卷主要包含了一元二次不等式在R,一元二次不等式在某区间,等式恒成立或能成立等内容,欢迎下载使用。
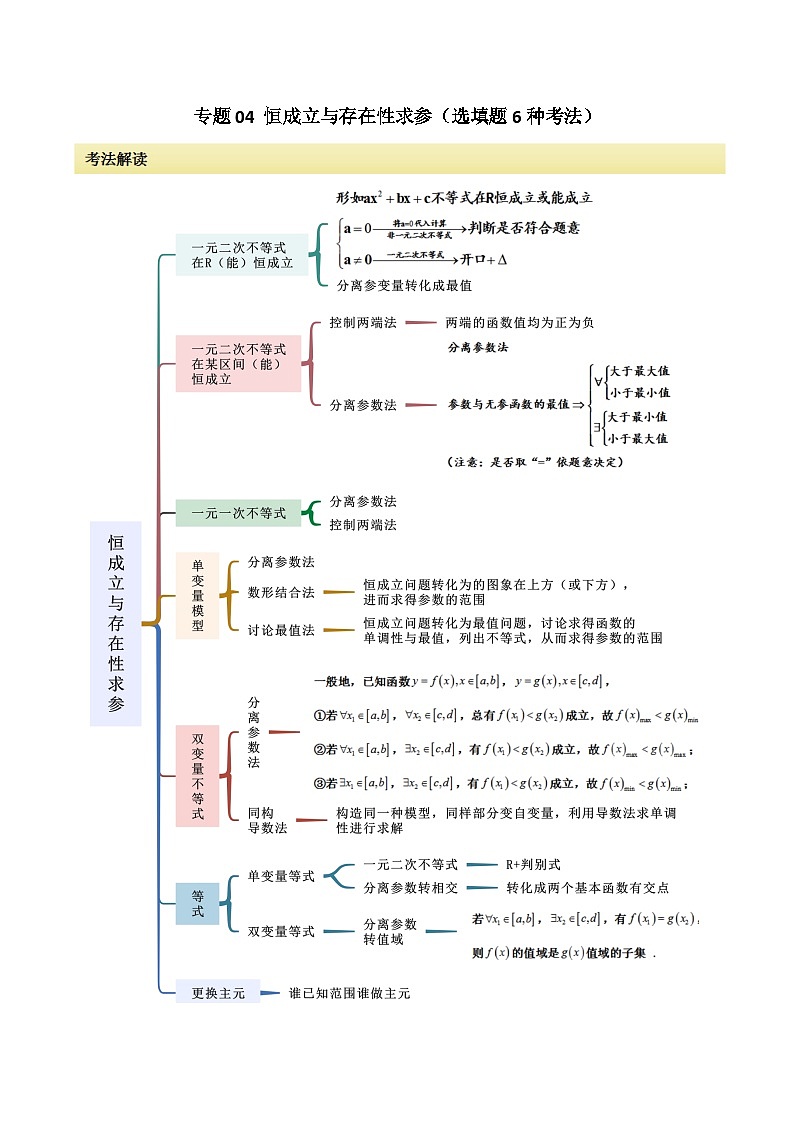
考法一 一元二次不等式在R
【例1-1】(2023·青海西宁·统考二模)已知命题:,,若p为假命题,则实数a的取值范围为( )
A.B.C.D.
【例1-2】(2023·四川·校联考模拟预测)“”是“,是假命题”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【例1-3】(2023·全国·高三对口高考)已知命题,使得“成立”为真命题,则实数a的取值范围是 .
【变式】
1.(2023·四川广安·四川省广安友谊中学校考模拟预测)若命题:“,使”是假命题,则实数m的取值范围为 .
2.(2023秋·江苏连云港·高三校考阶段练习)若不等式对任意实数均成立,则实数的取值范围是
3.(2023·广东潮州)若命题:“,使”是真命题,则实数m的取值范围为 .
考法二 一元二次不等式在某区间
【例2-1】(2023·河南·长葛市第一高级中学统考模拟预测)已知命题“,”为真命题,则实数的取值范围是( )
A.B.C.D.
【例2-2】(2023·陕西咸阳·武功县普集高级中学校考模拟预测)若命题“,使成立”的否定是真命题,则实数的取值范围是( )
A.B.
C.D.
【例2-3】(2023·辽宁大连)(多选)已知p:,,则使p为真命题的一个必要不充分条件为( )
A.B.C.D.
【例2-4】(2023秋·湖北宜昌)若对一切恒成立,则实数的取值范围是( )
A.B.C.D.
【变式】
1.(2023春·河北衡水·高三河北衡水中学校考阶段练习)若命题“”是假命题,则实数的最大值为______.
3.(2022秋·北京·高三统考阶段练习)若存在,有成立,则实数a的取值范围是__________.
2.(2022秋·重庆沙坪坝·高三重庆市凤鸣山中学校考阶段练习)若时,恒成立,则a的取值范围为______.
3.(2023·全国·高三对口高考)对于总有成立,则实数a的最小值为 .
4.(2023秋·安徽铜陵·高三统考阶段练习)若命题“,使得”是假命题,则的取值范围是 .
考法三 单变量的恒成立或能成立
【例3-1】(2023·全国·高三对口高考)若存在负实数使得方程成立,则实数a的取值范围是( )
A.B.C.D.
【例3-2】(2023·江苏南通·三模)若“”为假命题,则的取值范围为( )
A.B.C.D.
【例3-3】(2023·吉林·吉林省实验校考模拟预测)已知命题.若为假命题,则的取值范围为 .
【例3-4】(2023秋·河南郑州·高三郑州外国语学校校考阶段练习)若不等式对任意成立,则实数的最小值为 .
【变式】
1.(2023·四川成都·成都七中校考模拟预测)命题“,使得”为假命题,则a的取值范围为 .
2.(2023·全国·高三专题练习)已知函数,则 ;若对任意的,都有成立,则实数的取值范围为 .
3.(2023·全国·高三专题练习)若命题“,使得成立.”为假命题,则实数的最大值为?
考法四 双变量的恒成立或能成立
【例4-1】(2023·辽宁大连)已知,若存在,使对任意的,有成立,则实数m的取值范围是 .
【例4-2】(2023秋·江苏·高三宿迁中学校联考开学考试)已知为自然对数的底数,若对任意的,总存在唯一的,使得成立,则实数的取值范围是 .
【变式】
1.(2023秋·湖南衡阳·高三衡阳市田家炳实验中学校考阶段练习)已知,,,使成立.则a的取值范围( )
A.B.
C.D.
2.(2023·全国·高三专题练习)已知,且对都有成立,则实数的范围为
3(2023秋·重庆·高三统考阶段练习)已知,,若对,使成立,则实数的取值范围是 .
考法五 等式恒成立或能成立
【例5-1】(2023秋·福建三明·高三统考期末)已知函数,,设为实数,若存在实数,使得成立,则的取值范围为( )
A.B.
C.D.
【例5-2】(2023秋·江苏盐城·高三江苏省建湖高级中学校考阶段练习)已知函数,.若,,使得成立,则实数的取值范围为( )
A.B.
C.D.
【变式】
1.(2023秋·上海嘉定·高三上海市嘉定区第一中学校考开学考试)已知函数的表达式为,若对于任意,都存在,使得成立,则实数的取值范围是 .
2(2023秋·江苏镇江·高三统考开学考试)已知函数,若,,使得成立,则实数的取值范围为 .
考法六 更换主元
【例6】(2024秋·吉林通化·高三校考阶段练习)若,使得成立,则实数取值范围是( )
A.B.C.D.
【变式】
1.(2023秋·广东珠海)若,为真命题,则的取值范围为( )
A.B.
C.D.
2.(2023·北京)已知关于的不等式.若不等式对于恒成立,求实数x的取值范围
一.单选题
1.(2023·辽宁大连·大连二十四中校考模拟预测)命题“”为假命题,则命题成立的充分不必要条件是( )
A.B.C.D.
2(2023·重庆·统考模拟预测)命题“”是真命题的一个必要不充分条件是( )
A.B.C.D.
3.(2023·江苏淮安·江苏省盱眙中学校考模拟预测)已知.若p为假命题,则a的取值范围为( )
A.B.C.D.
4.(2023·四川绵阳·绵阳南山中学实验学校校考一模)若“,使成立”是假命题,则实数的取值范围是( )
A.B.C.D.
5.(2023秋·广西河池·高三校考开学考试)若命题“,使得成立”是假命题,则实数的取值范围是( )
A.B.C.D.
6.(2022秋·河南洛阳·高三洛阳市第一高级中学校考阶段练习)已知函数,若存在,使得有解,则实数a的取值范围是( )
A.B.
C.D.
7.(2023·江西上饶·高三校联考阶段练习)已知向量、满足,与的夹角为,若存在实数,有解,则的取值范围是( )
A.B.C.D.
8.(2023·全国·模拟预测)已知.若存在,使不等式有解,则实数m的取值范围为( )
A.B.C.D.
9.(2020·黑龙江绥化·统考模拟预测)已知函数,存在,使得不等式有解,则实数m的最小值为( )
A.0B.C.1D.2
10.(2023·全国·高三专题练习)设函数(其中为自然对数的底数),若存在实数a使得恒成立,则实数m的取值范围是( )
A.B.
C.D.
11.(2023·全国·高三专题练习)已知函数,若存在,使得)恒成立,则实数的取值范围是( )
A.B.C.D.
12.(2023·安徽滁州)若存在实数,对任意实数,使不等式恒成立,则的取值范围为( )
A.B.m<1C.D.
二、多选题
13.(2023·重庆九龙坡)已知函数是定义在上的奇函数,当时,.则下列结论正确的是( )
A.当时,B.函数有四个零点
C.若关于的方程有解,则实数的取值范围是D.对,恒成立
14.(2023·湖北武汉 )定义在上的函数满足:,,则关于不等式的表述正确的为( )
A.解集为B.解集为
C.在上有解D.在上恒成立
15.(2023·广东惠州)函数为定义在R上的奇函数,当时,,下列结论正确的有( )
A.当时,
B.函数有且仅有2个零点
C.若,则方程在上有解
D.,恒成立
16.(2023春·重庆沙坪坝·高三重庆八中校考阶段练习)若函数,则存在(其中,且),使下列式子对任意的恒成立的是( )
A.B.
C.D.
17.(2022·湖南岳阳·岳阳一中校考一模)已知函数,,若存在,使得对任意,恒成立,则下列结论正确的是( )
A.对任意,
B.存在,使得
C.存在,使得在上有且仅有1个零点
D.存在,使得在上单调递减
三、填空题
18.(2023·湖北黄冈·统考模拟预测)若“使”为假命题,则实数的取值范围为 .
19.(2023·宁夏银川·校考模拟预测)若命题“,”为假命题,则实数的取值范围是 .
20.(2023·陕西宝鸡·统考一模)若命题“”是假命题,则实数的取值范围是 .
21.(2022秋·上海浦东新·高三上海市洋泾中学校考阶段练习)若存在,使得不等式有解,则实数的取值范围为 .
22.(2022秋·上海虹口·高三统考阶段练习)设,若存在唯一的m使得关于x的不等式组有解,则a的取值范围是 .
23.(2022秋·广东汕头·高三金山中学校考阶段练习)已知,若存在常数,使恒成立,则的取值范围是 .
24.(2022秋·河南·高三校联考开学考试)已知数列的首项,且满足.若对于任意的正整数,存在,使得恒成立,则的最小值是 .
25.(2023·全国·高三专题练习)已知a>b,关于x的不等式对于一切实数x恒成立,又存在实数,使得成立,则最小值为 .
26.(2022秋·天津南开·高三南开中学校考阶段练习)已知,函数若存在实数,使得恒成立,则的最大值是 .
27.(2023·全国·高三专题练习)已知函数,若对任意,存在使得恒成立,则实数a的取值范围为 .
28.(2023秋·江苏镇江·高三江苏省镇江中学校考阶段练习)已知,若存在,使不等式,对于恒成立,则实数的取值范围是 .
293.(2022春·安徽淮南·高三寿县第一中学校考阶段练习)对,存在实数使得不等式恒成立,则的取值范围为
30.(2022·全国·高三专题练习)已知任意,若存在实数b使不等式对任意的恒成立,则b的最小值为 .
31.(2022·全国·高三专题练习)定义在R上的函数,若存在实数x使不等式对任意恒成立,则实数a的取值范围为 .
32.(2022·全国·高三专题练习)已知,存在实数,,使得恒成立,则的最大值与的最小值的积为 .
33.(2023·全国·高三专题练习)若关于x的不等式,对任意的实数,总存在实数使不等式恒成立,则实数a的取值范围是 .
34.(2022·全国·高三专题练习)存在使对任意的恒成立,则的最小值为 .
35.(2023·全国·高三专题练习)设数列满足,若存在常数,使得恒成立,则的最小值是
专题04 恒成立与存在性求参(选填题6种考法)
考法一 一元二次不等式在R
【例1-1】(2023·青海西宁·统考二模)已知命题:,,若p为假命题,则实数a的取值范围为( )
A.B.C.D.
【答案】D
【解析】因为命题:,,所以:,,
又因为为假命题,所以为真命题,即,恒成立,
所以,即,解得,故选:D.
【例1-2】(2023·四川·校联考模拟预测)“”是“,是假命题”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【解析】由题意,命题“,是假命题”
可得命题“,是真命题”
当时,即时,不等式恒成立;
当时,即时,则满足,解得,
综上可得,实数,
即命题“,是假命题”时,实数的取值范围是,
又由“”是“”的必要不充分条件,
所以“”是“,是假命题”的必要不充分条件,
故选:B.
【例1-3】(2023·全国·高三对口高考)已知命题,使得“成立”为真命题,则实数a的取值范围是 .
【答案】
【解析】因为命题,使得“成立”为真命题,
当时,,则,故成立;
当时,,解得:;
当时,总存在;
综上所述:实数a的取值范围为.
故答案为:
【变式】
1.(2023·四川广安·四川省广安友谊中学校考模拟预测)若命题:“,使”是假命题,则实数m的取值范围为 .
【答案】
【解析】由题意可知:命题:,.是真命题,
①当时,结论显然成立;
②当时,则,解得;
故答案为:.
2.(2023秋·江苏连云港·高三校考阶段练习)若不等式对任意实数均成立,则实数的取值范围是
【答案】
【解析】因为不等式对任意实数均成立,
即不等式对任意实数均成立,
当,即时,有恒成立,满足题意;
当,即时,则有,解得,
综上所述,实数的取值范围为.故选:B.
3.(2023·广东潮州)若命题:“,使”是真命题,则实数m的取值范围为 .
【答案】
【解析】当时,易得m=1时命题成立;
当时,
当时,则命题等价于,
故答案为:
考法二 一元二次不等式在某区间
【例2-1】(2023·河南·长葛市第一高级中学统考模拟预测)已知命题“,”为真命题,则实数的取值范围是( )
A.B.C.D.
【答案】C
【解析】因为命题“,”为真命题,
所以,命题“,”为真命题,
所以,时,,
因为,,
所以,当时,,当且仅当时取得等号.
所以,时,,即实数的取值范围是
故选:C
【例2-2】(2023·陕西咸阳·武功县普集高级中学校考模拟预测)若命题“,使成立”的否定是真命题,则实数的取值范围是( )
A.B.
C.D.
【答案】C
【解析】若“,使成立”的否定是:
“,使”为真命题,即;令,
由,得,所以,所以,故选:C.
【例2-3】(2023·辽宁大连)(多选)已知p:,,则使p为真命题的一个必要不充分条件为( )
A.B.C.D.
【答案】AC
【解析】令,则的图象开口向上,
若,,则,解得,
对于A,当时,成立,而时,不一定成立,
所以是p为真命题的一个必要不充分条件,所以A正确,
对于B,是p为真命题的充要条件,所以B错误,
对于C,当时,成立,当时,不一定成立,
所以是p为真命题的一个必要不充分条件,所以C正确,
对于D,当时,不一定成立,当时,成立,
所以是p为真命题的一个充分不必要条件,所以D错误,
故选:AC
【例2-4】(2023秋·湖北宜昌)若对一切恒成立,则实数的取值范围是( )
A.B.C.D.
【答案】B
【解析】因为不等式(),
所以或(),
①当时,,
所以不等式的解集为,
所以原不等式不可能对一切恒成立,故不符合题意;
②当时,,
所以不等式的解集为或,
又因为原不等式对一切恒成立,
所以,解得,
③当时,,
所以不等式的解集为或,
又因为原不等式对一切恒成立,
所以,解得,
综述,.
故选:B.
【变式】
1.(2023春·河北衡水·高三河北衡水中学校考阶段练习)若命题“”是假命题,则实数的最大值为______.
【答案】
【解析】由题知命题的否定“”是真命题.令,则 解得,故实数的最大值为
故答案为:
3.(2022秋·北京·高三统考阶段练习)若存在,有成立,则实数a的取值范围是__________.
【答案】
【解析】将原不等式参数分离可得,设,
已知存在,有成立,则,
令,则,,
由对勾函数知在
上单调递减,在上单调递增,
,,
所以,即,
故答案为:.
2.(2022秋·重庆沙坪坝·高三重庆市凤鸣山中学校考阶段练习)若时,恒成立,则a的取值范围为______.
【答案】
【解析】解法1:时,恒成立,
即恒成立,即恒成立.
令(),则,,
当且仅当,即,等号成立,
故,即a的取值范围为.
解法2:令,
则由题意知,,在时恒成立,即时,.
①当,即时,在单调递增,
此时,成立,
所以,恒成立;
②当,即时,在上单调递减,
在单调递增,所以,
此时只需,即可,即
解得,,∴,
综上所述,a的取值范围为.
故答案为:.
3.(2023·全国·高三对口高考)对于总有成立,则实数a的最小值为 .
【答案】4
【解析】由题意可得,
当时,在上恒成立,
故在上单调递减,则,不合题意;
当时,,
由于,故在上恒成立,
仅当时,等号成立,
则在上单调递减,则,不合题意;
当时,,
由于,故在上单调递增,
在上单调递减,
故令,解得,
故实数a的最小值为4,故答案为:4
4.(2023秋·安徽铜陵·高三统考阶段练习)若命题“,使得”是假命题,则的取值范围是 .
【答案】
【解析】由题意原命题的否定“,使得”是真命题,
不妨设,其开口向上,对称轴方程为,
则只需在上的最大值即可,我们分以下三种情形来讨论:
情形一:当即时,在上单调递增,
此时有,解得,
故此时满足题意的实数不存在;
情形二:当即时,在上单调递减,在上单调递增,
此时有,只需,
解不等式组得,
故此时满足题意的实数的范围为;
情形三:当即时,在上单调递减,
此时有,解得,故此时满足题意的实数不存在;
综上所述:的取值范围是.故答案为:.
考法三 单变量的恒成立或能成立
【例3-1】(2023·全国·高三对口高考)若存在负实数使得方程成立,则实数a的取值范围是( )
A.B.C.D.
【答案】C
【解析】由题意可得:,
令,因为,在上均为增函数,
所以在为增函数,且,,,
所以,所以实数a的取值范围是.
故选:C.
【例3-2】(2023·江苏南通·三模)若“”为假命题,则的取值范围为( )
A.B.C.D.
【答案】A
【解析】依题意知命题“”为假命题,
则“”为真命题,
所以,则,
解得,所以的取值范围为.故选:A
【例3-3】(2023·吉林·吉林省实验校考模拟预测)已知命题.若为假命题,则的取值范围为 .
【答案】
【解析】为假命题
为真命题,故,
令,则,
令解得,令解得,
所以在上单调递减,在上单调递增,所以,所以.
故答案为:.
【例3-4】(2023秋·河南郑州·高三郑州外国语学校校考阶段练习)若不等式对任意成立,则实数的最小值为 .
【答案】
【解析】因为对任意成立,
不等式可变形为:,即,
即对任意成立,
记,则,所以在上单调递增,
则可写为,
根据单调性可知,只需对任意成立即可,
即成立,记,即只需,
因为,故在上,,单调递增,
在上,,单调递减,所以,
所以只需即可,解得.故答案为:
【变式】
1.(2023·四川成都·成都七中校考模拟预测)命题“,使得”为假命题,则a的取值范围为 .
【答案】
【解析】若“,使得”为假命题,
可得当时,恒成立,只需.
又函数在上单调递增,所以.
故答案为:
2.(2023·全国·高三专题练习)已知函数,则 ;若对任意的,都有成立,则实数的取值范围为 .
【答案】
【解析】,
对任意,都有成立,即|,
画出函数的图象,如图所示
观察的图象可知,当时,函数,
所以,解得或,
∴实数k的取值范围为.答案:;.
3.(2023·全国·高三专题练习)若命题“,使得成立.”为假命题,则实数的最大值为?
【答案】
【解析】由题意得知命题“,成立”.
(1)当时,不等式成立;
(2)当时,由,则,
不等式两边取自然对数得,可得,
构造函数,其中,则,
令,得,当时,,
所以函数在区间上单调递减,则,
所以,因此实数的最大值为.
考法四 双变量的恒成立或能成立
【例4-1】(2023·辽宁大连)已知,若存在,使对任意的,有成立,则实数m的取值范围是 .
【答案】
【解析】当时,.当时,.
若存在,使对任意的,有成立,
等价于,可得,所以.
故答案为:
【例4-2】(2023秋·江苏·高三宿迁中学校联考开学考试)已知为自然对数的底数,若对任意的,总存在唯一的,使得成立,则实数的取值范围是 .
【答案】
【解析】由,得,
令,求导得,
当时,,函数在上单调递减,函数值从减小到0,
当时,,函数在上单调递增,函数值从0增大到,
令,显然函数在上单调递减,函数的值域为,
由对任意的,总存在唯一的,使得成立,得,
因此,解得,
所以实数的取值范围是.
【变式】
1.(2023秋·湖南衡阳·高三衡阳市田家炳实验中学校考阶段练习)已知,,,使成立.则a的取值范围( )
A.B.
C.D.
【答案】B
【解析】由题设,使成立,
所以在上成立,
对于,有,
对于,有,
所以,即,可得.故选:B
2.(2023·全国·高三专题练习)已知,且对都有成立,则实数的范围为
【答案】
【解析】由题意,函数,
要使得,即,即对恒成立,
即对恒成立,
令,可得,
当时,,单调递增;当时,,单调递减,
所以函数在单调递减,在单调递增,
所以,即,即,当且仅当时,等号成立,
设,则在上为增函数,
而,,故在上存在零点,
故,当且仅当时等号成立,
即,所以,
即实数的取值范围是.
3(2023秋·重庆·高三统考阶段练习)已知,,若对,使成立,则实数的取值范围是 .
【答案】
【解析】令,则,即,
所以(为辅助角,),
故,即,解得.
由题可知,,,即对,.
令,令,则,
当时,的最小值为,即,
则,即,
故答案为:
考法五 等式恒成立或能成立
【例5-1】(2023秋·福建三明·高三统考期末)已知函数,,设为实数,若存在实数,使得成立,则的取值范围为( )
A.B.
C.D.
【答案】D
【解析】当时, .
令 ,由于 且 ,所以 或,所以
的取值范围是;
当时, ,的取值范围是,;
综上可得的取值范围是,;
要存在实数,使得成立,则函数,
即,即,解得:.故选:D
【例5-2】(2023秋·江苏盐城·高三江苏省建湖高级中学校考阶段练习)已知函数,.若,,使得成立,则实数的取值范围为( )
A.B.
C.D.
【答案】C
【解析】设函数在上的值域为,函数在上的值域为,
因为若,,使得成立,所以,
因为,,所以在上的值域为,
因为,
当时,在上单调递减,所以在上的值域为,
因为,所以,解得,又,所以此时不符合题意,
当时,图像是将下方的图像翻折到轴上方,
令得,即,
①当时,即时,在,上单调递减,
,,所以的值域,
又,所以,解得,
②当时,即时,在上单调递减,在
上单调递增,
,或,
所以的值域或,又,所以或,
当时,解得或,又,所以,
当时,解得或,又,所以,所以的取值范围.
③当时,时,在上单调递增,
所以,,所以在上的值域,
又,所以,解得,综上所述,的取值范围为.
故选:C
【变式】
1.(2023秋·上海嘉定·高三上海市嘉定区第一中学校考开学考试)已知函数的表达式为,若对于任意,都存在,使得成立,则实数的取值范围是 .
【答案】
【解析】在上单调递增,
当时,,,
,,即,
故是值域的子集,故,解得.
故答案为:.
2(2023秋·江苏镇江·高三统考开学考试)已知函数,若,,使得成立,则实数的取值范围为 .
【答案】
【解析】设在上的值域为,在上的值域为,
若,,使得成立,则.
1.当时,则,
可知开口向下,对称轴为,
则在上单调递增,可得,
所以在上的值域为,所以;
2.当时,则,
(1)若,则在内单调递减,
且当x趋近于0时,趋近于,当x趋近于时,趋近于,
所以,符合题意;
(2)若,则,即,不合题意;
(3)若,则,
令,解得;令,解得;
则在上单调递增,在上单调递减,可得,
且当x趋近于0或时,均趋近于,所以,
又因为,则,
注意到,即,解得;
综上所述:实数的取值范围为.
故答案为:.
考法六 更换主元
【例6】(2024秋·吉林通化·高三校考阶段练习)若,使得成立,则实数取值范围是( )
A.B.C.D.
【答案】B
【解析】若,使得成立,
则,即,
当时,成立,
当时,令,在上单调递增,
即,则,解得:,
因为,所以,
当时,令,在上单调递减,
即,则,解得:,
因为,所以,综上:实数取值范围是.故选:B.
【变式】
1.(2023秋·广东珠海)若,为真命题,则的取值范围为( )
A.B.
C.D.
【答案】C
【解析】由题意知,,恒成立,
设函数,
即,恒成立.
则,即,
解得,或.
故选:C.
2.(2023·北京)已知关于的不等式.若不等式对于恒成立,求实数x的取值范围
【答案】
【解析】由题知,
设,
当时,恒成立.
当且仅当,即,
解得且,
或且,
则.
所以的取值范围是.
一.单选题
7.(2023·辽宁大连·大连二十四中校考模拟预测)命题“”为假命题,则命题成立的充分不必要条件是( )
A.B.C.D.
【答案】C
【解析】因为命题“”为假命题,所以,对,恒成立,
当时,在上恒成立,所以满足条件,
当时,令,对称轴,且,所以,当时,恒成立,
当时,显然有不恒成立,
故对,恒成立时,,所以则命题成立的充分不必要条件是选项C.
故选:C.
2(2023·重庆·统考模拟预测)命题“”是真命题的一个必要不充分条件是( )
A.B.C.D.
【答案】A
【解析】若命题“”是真命题,则,
可知当时,取到最大值,解得,
所以命题“”是真命题等价于“”.
因为,故“”是“”的必要不充分条件,故A正确;
因为,故“”是“”的充要条件,故B错误;
因为,故“”是“”的充分不必要条件,故C错误;
因为与不存在包含关系,故“”是“”的即不充分也不必要条件,故D错误;
故选:A.
3.(2023·江苏淮安·江苏省盱眙中学校考模拟预测)已知.若p为假命题,则a的取值范围为( )
A.B.C.D.
【答案】A
【解析】因为p为假命题,所以,为真命题,
故当时,恒成立.
因为当时,的最小值为,
所以,即a的取值范围为.
故选:A.
4.(2023·四川绵阳·绵阳南山中学实验学校校考一模)若“,使成立”是假命题,则实数的取值范围是( )
A.B.C.D.
【答案】C
【解析】若“,使成立”是假命题,则“,使成立”是真命题,即,;
令,则,则在上单增,,则.
故选:C.
5.(2023秋·广西河池·高三校考开学考试)若命题“,使得成立”是假命题,则实数的取值范围是( )
A.B.C.D.
【答案】D
【解析】命题“,使得成立”的否定为:,,
依题意,命题“,”为真命题,
当时,,而,
当且仅当,即时取等号,因此,
所以实数的取值范围是.
故选:D
6.(2022秋·河南洛阳·高三洛阳市第一高级中学校考阶段练习)已知函数,若存在,使得有解,则实数a的取值范围是( )
A.B.
C.D.
【答案】C
【解析】若存在,使得有解,
由函数,即,即在有解,
设,可得,
当时,,单调递增;
当时,,单调递减,
所以当时,函数取得极大值,也为最大值,即,
所以,即实数a的取值范围是.
故选:C.
7.(2023·江西上饶·高三校联考阶段练习)已知向量、满足,与的夹角为,若存在实数,有解,则的取值范围是( )
A.B.C.D.
【答案】C
【解析】对不等式两边同时平方,
得,即,
因为,
所以,
整理得有解,
所以得,
解得,又因为,所以,
故选:C.
8.(2023·全国·模拟预测)已知.若存在,使不等式有解,则实数m的取值范围为( )
A.B.C.D.
【答案】B
【解析】
,
若存在,使不等式有解,
则问题转化为在上
因为,所以,
所以,
所以,
解得:或
即实数m的取值范围为:,
故选:B.
9.(2020·黑龙江绥化·统考模拟预测)已知函数,存在,使得不等式有解,则实数m的最小值为( )
A.0B.C.1D.2
【答案】A
【解析】.
由,得,设,则,
当时,;当时,,从而在上递增,在上递减,∴,
当时,,即,
在上,,.递减;在上,,,递增,
,设,
∴,,∴在上递减,,∴m的最小值为0.
故选:A.
10.(2023·全国·高三专题练习)设函数(其中为自然对数的底数),若存在实数a使得恒成立,则实数m的取值范围是( )
A.B.
C.D.
【答案】A
【解析】函数的定义域为,
由,得,所以,
令,
由题意知,函数和函数的图象,一个在直线上方,一个在直下方,等价于一个函数的最小值大于另一个函数的最大值,
由,得,
所以当时,单调递增,
当时,单调递减,
所以,没有最小值,
由,得,
当时,在上单调递增,
在上单调递减,
所以有最大值,无最小值,不合题意,
当时,在上单调递减,
在上单调递增,
所以,
所以即,
所以,即m的取值范围为.
故选:A.
11.(2023·全国·高三专题练习)已知函数,若存在,使得)恒成立,则实数的取值范围是( )
A.B.C.D.
【答案】A
【解析】存在,使得恒成立,
是函数的最小值点,
若,当时,;当时,,此时不存在,使得,不合题意;
若,的对称轴为,函数在,上单调递增,;
在上,,则没有最小值,不符合题意;
若,的对称轴为,函数在,上;
函数在上,,要使存在,使得恒成立,
则,即,解得或,
又,,即实数的取值范围是,.
故选:A.
12.(2023·安徽滁州)若存在实数,对任意实数,使不等式恒成立,则的取值范围为( )
A.B.m<1C.D.
【答案】D
【解析】由,得,
时,不等式不可能对恒成立,∴.
作函数和的图象,如图,
时,不等式对不可能恒成立,
在不全为0时,对,的图象是一条线段,这条线段只能是或在其下方(其中),线段的方程是,
要使得原命题成立,只要函数的图象在线段下方即可,即,,
当时,,∴.故选:D.
二、多选题
13.(2023·重庆九龙坡)已知函数是定义在上的奇函数,当时,.则下列结论正确的是( )
A.当时,B.函数有四个零点
C.若关于的方程有解,则实数的取值范围是D.对,恒成立
【答案】AD
【解析】对于A选项:当x>0时,﹣x<0,
所以f(x)=﹣f(﹣x)=﹣e﹣x(﹣x+2)=e﹣x(x﹣2),故A正确;
对于B选项:当x<0时,f(x)=ex(x+2),令f(x)=0⇒x=﹣2,即小于0的零点只有1个,根据奇函数对称性可知大于0的零点也只有一个,
又因为f(x)是定义在R上的奇函数,故0也是函数f(x)的零点,于是函数f(x)的零点共有3个,故B不正确;
对于C选项:当x<0时,f′(x)=ex(x+3),
∴x<﹣3时,f′(x)<0,﹣3<x<0时,f′(x)>0,
∴f(x)在(﹣∞,﹣3)上单调递减,在(﹣3,0)上单调递增,
∴x=﹣3时,f(x)取最小值﹣e﹣3,且x<﹣3时,f(x)<0,
﹣3<x<0时,f(x)<2,即﹣e﹣3≤f(x)<2;
当x>0时,f′(x)=e﹣x(3﹣x),
∴f(x)在(0,3)上单调递增,在(3,+∞)上单调递减,
x=3时,f(x)取最大值e﹣3,且x>3时,f(x)>0,
0<x<3时,f(x)>﹣2,∴﹣2<f(x)≤e﹣3,且f(0)=0,
∴﹣2<f(x)<2,∴f(x)的值域为(﹣2,2),故C不正确;
对于D选项:结合C的结论可知∴∀x1,x2∈R,都有|f(x1)﹣f(x2)|<4,故D正确.
故选:AD.
14.(2023·湖北武汉 )定义在上的函数满足:,,则关于不等式的表述正确的为( )
A.解集为B.解集为
C.在上有解D.在上恒成立
【答案】AC
【解析】令,,则,
∵,
∴恒成立,即在上单调递增.
∵,
∴.
不等式可化为,等价于,
∴,即不等式式的解集为,
则在上有解,故选项AC正确.
故选:AC.
15.(2023·广东惠州)函数为定义在R上的奇函数,当时,,下列结论正确的有( )
A.当时,
B.函数有且仅有2个零点
C.若,则方程在上有解
D.,恒成立
【答案】AD
【解析】A.函数为定义在R上的奇函数,当时,,,A正确;
B.当时,,解得,时,,解得,又,所以有和0三个零点,B错误;
C.当时,,,当时,,递减,时,,递增,
∴时,极小值=,
时,,,,
由是奇函数,∴时,极大值=,,的值域是,若时,方程在时无解,C错误;
D.由C的讨论知,因此对任意的实数有,,∴,即.D正确.
故选:AD.
16.(2023春·重庆沙坪坝·高三重庆八中校考阶段练习)若函数,则存在(其中,且),使下列式子对任意的恒成立的是( )
A.B.
C.D.
【答案】ABC
【解析】,当时,,则在上单调递增,又,
∴,∴A正确;此时,,则,
∴,∴B正确;
由,则
当时C式子成立,∴C正确;
若任意满足,则函数关于点对称,但是的唯一对称中心为,∴D错误,
故选:ABC
17.(2022·湖南岳阳·岳阳一中校考一模)已知函数,,若存在,使得对任意,恒成立,则下列结论正确的是( )
A.对任意,
B.存在,使得
C.存在,使得在上有且仅有1个零点
D.存在,使得在上单调递减
【答案】AD
【解析】,其中,,为锐角,
恒成立,则是的最大值,是其函数图象的一条对称轴,因此,A正确;
的周期是,因此是最小值点,B错;
,则时,,时,,
所以时,,,在上恒为0,有无数个零点,C错;
由的定义知其在上递减,在上递增,
所以当时,,D正确.
故选:AD.
三、填空题
18.(2023·湖北黄冈·统考模拟预测)若“使”为假命题,则实数的取值范围为 .
【答案】
【解析】因为“使”为假命题,
所以“,”为真命题,
其等价于在上恒成立,
又因为对勾函数在上单调递减,在上单调递增,
而,所以,
所以,即实数的取值范围为.
故答案为:.
19.(2023·宁夏银川·校考模拟预测)若命题“,”为假命题,则实数的取值范围是 .
【答案】
【解析】“,”是假命题,
则它的否定命题:“,”是真命题;
所以,,恒成立,所以,
即实数的取值范围是.
故答案为:.
20.(2023·陕西宝鸡·统考一模)若命题“”是假命题,则实数的取值范围是 .
【答案】
【解析】命题“”的否定为:“,”.
因为原命题为假命题,则其否定为真.当时显然不成立;当时,恒成立;当时,只需,解得:.综上有故答案为:.
21.(2022秋·上海浦东新·高三上海市洋泾中学校考阶段练习)若存在,使得不等式有解,则实数的取值范围为 .
【答案】
【解析】设,
则,
当且仅当,即,即时,等号成立,
又,所以,显然存在.
所以,最小值为9.
要使不等式有解,只需要即可,即,去绝对值可得或,所以或.
故答案为:.
22.(2022秋·上海虹口·高三统考阶段练习)设,若存在唯一的m使得关于x的不等式组有解,则a的取值范围是 .
【答案】
【解析】依题意,,由不等式有解知,,而,因此,
因存在唯一的m使得关于x的不等式组有解,
则当且仅当时,不等式组有解,且当时不等式组无解,
由有解得有解,于是得,解得,
由无解得无解,于是得,解得,因此,
所以a的取值范围是.故答案为:
23.(2022秋·广东汕头·高三金山中学校考阶段练习)已知,若存在常数,使恒成立,则的取值范围是 .
【答案】
【解析】使恒成立,则,
化简整理得,
由于存在常数,使恒成立,
可知,
因此,解得.
故答案为:
24.(2022秋·河南·高三校联考开学考试)已知数列的首项,且满足.若对于任意的正整数,存在,使得恒成立,则的最小值是 .
【答案】3
【解析】数列满足,且,即,
当时,,
当时,,
当时,,
当时,,
以上各式相加,得
又,,
,,
若对于任意的正整数,存在,使得恒成立,则有,
的最小值是3.
故答案为:.
25.(2023·全国·高三专题练习)已知a>b,关于x的不等式对于一切实数x恒成立,又存在实数,使得成立,则最小值为 .
【答案】
【解析】因为对于一切实数恒成立,
所以,且,所以;
再由,使成立,
可得,所以,
所以,
因为,即,所以,
当且仅当,即时,等号成立,
所以的最小值为,
故答案为:
26.(2022秋·天津南开·高三南开中学校考阶段练习)已知,函数若存在实数,使得恒成立,则的最大值是 .
【答案】/0.625
【解析】由题意得:,①当,即时,;
②当,即时,,
当即时,;
当即时,,
当即时,;
③当时,,此时.
则当时,;
当时,,画出在的图象,
令,解得,此时相切,可得;
当时,;则,
即当时,,又,则;
当时,,又,则;
当时,,又,则;
综上可得,即的最大值是.
故答案为:.
27.(2023·全国·高三专题练习)已知函数,若对任意,存在使得恒成立,则实数a的取值范围为 .
【答案】
【解析】根据题意可得只需即可,由题可知a为对数底数且或.当时,此时在各自定义域内都有意义,由复合函数单调性可知在上单调递减,在上单调递减,所以,,所以,即,可得;当时,由复合函数单调性可知在上单调递减,在上单调递增,所以,,所以,即,可得.综上:.
故答案为:.
28.(2023秋·江苏镇江·高三江苏省镇江中学校考阶段练习)已知,若存在,使不等式,对于恒成立,则实数的取值范围是 .
【答案】
【解析】时,不等式可化为,
因为存在使不等式恒成立,
所以只需,
设,,
则,,
所以在上为增函数,
所以,所以,,
所以整理可得,
设,
所以,令,
则,
所以在上单调递增,
所以,
所以,则在上单调递增,
所以,
所以,即实数的取值范围是
293.(2022春·安徽淮南·高三寿县第一中学校考阶段练习)对,存在实数使得不等式恒成立,则的取值范围为
【答案】
【解析】由题意可知,对,存在实数使得不等式恒成立,转化为在恒成立,
即,即可.
设,则.
令,即,解得,
当时,,所以函数在上单调递减;
当时,,所以函数在上单调递增;
当时,取得极大值,也为函数的最大值,
.
设,则.
令,即,解得,
当时,,所以函数在上单调递增;
当时,,所以函数在上单调递减;
当时,取得极小值,也为函数的最小值,
.
即,解得
所以的取值范围为.
故答案为:
30.(2022·全国·高三专题练习)已知任意,若存在实数b使不等式对任意的恒成立,则b的最小值为 .
【答案】6
【解析】由题意,
设,,其图象为开口向上,对称轴为的抛物线的一部分,
当,即时,,;
当,即时,,;
若要对于任意,均成立,则即,所以b的最小值为6.
故答案为:6
31.(2022·全国·高三专题练习)定义在R上的函数,若存在实数x使不等式对任意恒成立,则实数a的取值范围为 .
【答案】
【解析】因为存在实数x使不等式对任意恒成立,
所以,
而,则,
令,则,所以在上单调递增,且,
所以时,,即,故单调递减;时,,即,故单调递增;所以在处取得极小值也是最小值,故
,
因为不等式对任意恒成立,
时,不等式恒成立;
时,不等式等价于;令,则,故在上单调递增,故,所以,因此实数a的取值范围为.
故答案为:.
32.(2022·全国·高三专题练习)已知,存在实数,,使得恒成立,则的最大值与的最小值的积为 .
【答案】
【解析】如图过点时,最大,即
与相切时,最小,即
故
故答案为:
33.(2023·全国·高三专题练习)若关于x的不等式,对任意的实数,总存在实数使不等式恒成立,则实数a的取值范围是 .
【答案】
【解析】,即,即恒成立.
即,设,则.
当时,函数单调递增,当时,函数单调递减,故,
故.
故答案为:.
34.(2022·全国·高三专题练习)存在使对任意的恒成立,则的最小值为 .
【答案】
【解析】存在使对任意的恒成立,
则等价于等价于存在,,在的上方.
直线过定点,即定点在直线上,
设直线与相切于点,
,所以,
由得,
化简得,故.
构造函数,
则,
所以当时,,函数递减,
当时,,函数递增,
所以.所以的最小值为.
故答案为:
35.(2023·全国·高三专题练习)设数列满足,若存在常数,使得恒成立,则的最小值是 .
【答案】-2
【解析】由题意即可,
,
若,则且,即该数列单增,且,
此时若存在常数,使得恒成立,则必有.
若,则,该数列为常数列,即.
当时,显然有
综上所述,.
故答案为:
相关试卷
这是一份2024年高考数学二轮复习专题03平面向量(选填题10种考法)(原卷版+解析),共92页。试卷主要包含了平面向量的坐标运算,平面向量的基本定理,平面向量的数量积,平面向量的共线定理,平面向量中的取值范围,平面向量与四心,平面向量巧建坐标,平面向量与奔驰定理等内容,欢迎下载使用。
这是一份2024年高考数学二轮复习专题02复数(选填题10种考法)(原卷版+解析),共54页。试卷主要包含了复数的实部与虚部,共轭复数,相等复数,复数的模长,在复平面对应的象限,在复数的范围内解方程,与复数相关的轨迹,最值等内容,欢迎下载使用。
这是一份备战2024年高考数学二轮复习专题04利用导数解决恒成立与存在性问题(原卷版+解析),共34页。试卷主要包含了恒成立问题,存在性问题等内容,欢迎下载使用。









