2024年高考数学二轮复习专题06零点(选填题8种考法)(原卷版+解析)

这是一份2024年高考数学二轮复习专题06零点(选填题8种考法)(原卷版+解析)，共76页。试卷主要包含了零点区间，零点区间求参数，判断零点个数，根据零点个数求参数，零点之和，零点之和的范围，嵌套函数的零点等内容，欢迎下载使用。

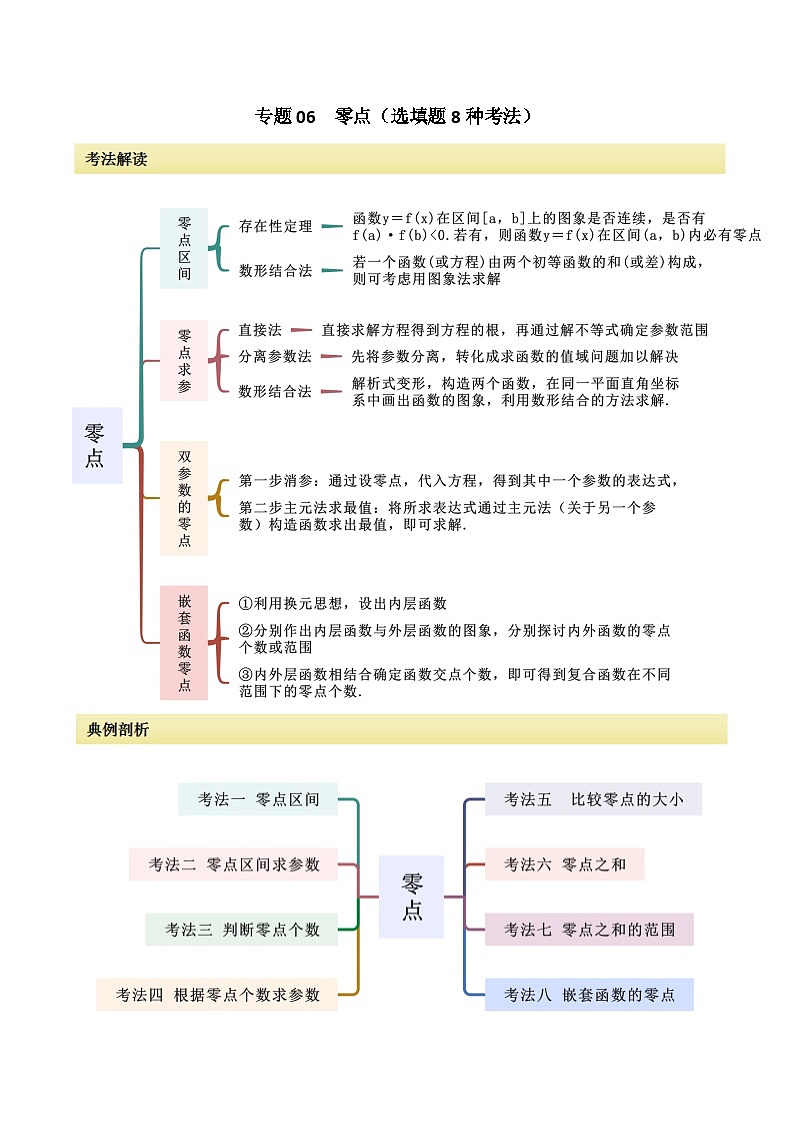
考法一 零点区间
【例1】（2023·吉林长春·东北师大附中校考一模）方程的根所在区间是（ ）
A．B．C．D．
【变式】
1．（2023·海南·模拟预测）函数的零点所在的大致区间为（ ）
A．B．C．D．
2．（2023·云南昆明·昆明一中校考模拟预测）函数的零点所在的区间为（ ）
A．B．
C．D．
3．（2023·广东梅州·统考二模）用二分法求方程近似解时，所取的第一个区间可以是（ ）
A．B．C．D．
考法二 零点区间求参数
【例2-1】（2023·宁夏银川·银川一中校考三模）函数在区间上存在零点，则实数的取值范围是（ ）
A．B．
C．D．
【例2-2】（2023·浙江绍兴·统考二模）已知函数，若在区间上有零点，则的最大值为 .
【变式】
1．（2023·北京·统考模拟预测）已知函数，若方程的实根在区间上，则k的最大值是（ ）
A．B．C．D．
2．（2023·安徽滁州·校考模拟预测）已知函数在区间上有零点，则实数m的取值范围是________．
3．（2023·吉林通化·梅河口市第五中学校考模拟预测）已知函数在区间上存在零点，则的最小值为 .
考法三 判断零点个数
【例3-1】（2023·河南·校联考模拟预测）函数的零点个数为（ ）
A．0B．1C．2D．3
【例3-2】．（2023·贵州黔东南·凯里一中校考模拟预测）函数在内零点的个数为（ ）
A．1B．2C．3D．4
【例3-3】（2023·河南·校联考模拟预测）设是定义在上的周期为5的奇函数，，则在内的零点个数最少是（ ）
A．4B．6C．7D．9
【变式】
1．（2023·山东潍坊·统考模拟预测）函数在区间上的零点个数是（ ）
A．3B．4C．5D．6
2．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知方程的解个数为（ ）
A．0B．1C．2D．3
3．（2023·江苏扬州·江苏省高邮中学校考模拟预测）已知函数 在 上单调递增，则f（x）在上的零点可能有（ ）
A．2个B．3个C．4个D．5个
4．（2023·宁夏银川·统考模拟预测）是定义在上的奇函数，当时，，，令，则函数的零点个数为（ ）
A．4B．5C．6D．7
5．（2023·江西上饶·统考一模）已知函数，则在上的零点个数是（ ）
A．2023B．2024C．2025D．2026
考法四 根据零点个数求参数
【例4-1】（2023·全国·统考高考真题）已知函数在区间有且仅有3个零点，则的取值范围是 ．
【例4-2】（2022·天津·统考高考真题）设，对任意实数x，记．若至少有3个零点，则实数的取值范围为 .
【变式】
1．（2023·广西梧州·校考一模）若函数在区间内恰有一个零点，则实数a的取值范围是 ．
2．（2023·江苏淮安·江苏省郑梁梅高级中学校考模拟预测）已知函数有三个零点，则a的取值范围是______.
3（2023春·湖北）设函数 在区间[上有零点，则实数的取值范围是___________.
4．（2023·山西·校联考模拟预测）已知函数有3个零点，则实数a的取值范围为 ．
考法五 比较零点的大小
【例5-1】（2022·安徽合肥·合肥市第六中学校考模拟预测）已知函数，，的零点分别为a，b，c则a，b，c的大小顺序为（ ）
A．B．
C．D．
【例5-2】（2023·江西南昌）已知函数，，的零点分别为，，，则（ ）．
A．B．
C．D．
【变式】
1．（2022·重庆沙坪坝·重庆南开中学校考模拟预测）已知实数a，b，c满足，则下列不等式一定不成立的为（ ）
A．B．C．D．
2．（2022·江西·校联考模拟预测）已知函数，，的零点分别是a，b，c，则a，b，c的大小顺序是（ ）
A．B．C．D．
3．（2023·陕西西安）已知函数，，的零点分别为、、，则、、的大小顺序为（ ）
A．B．
C．D．
考法六 零点之和
【例6-1】（2023·青海西宁·统考二模）函数的所有零点之和为（ ）
A．4B．5C．6D．7
【例6-2】（2023·河南·模拟预测）已知定义域为的函数满足，且曲线与曲线有且只有两个交点，则函数的零点之和是（ ）
A．2B．－2C．4D．－4
【变式】
1．（2023·河南·统考三模）已知函数是定义域为的偶函数，且满足，当时，，则关于的方程在上所有实数解之和为（ ）
A．9B．C．D．7
2．（2022·江西·江西师大附中校考三模）定义在R上的函数满足，且当时，.则函数的所有零点之和为（ ）
A．7B．14C．21D．28
3．（2023·湖北·校联考模拟预测）函数是定义在R上的奇函数，当时，，则函数在上的所有零点之和为（ ）
A．－32B．32C．16D．8
4．（2023·全国·模拟预测）已知定义在上的函数满足：为偶函数，且；函数，则当时，函数的所有零点之和为（ ）
A．B．C．D．
考法七 零点之和的范围
【例7-1】（2023·上海嘉定·校考三模）已知函数，若满足（、、互不相等），则的取值范围是（ ）
A．B．C．D．
【例7-2】．（2023·山东济宁·统考二模）已知函数，若，则的最小值是（ ）
A．B．C．D．
【变式】
1．（2023·吉林长春·东北师大附中校考模拟预测）已知函数，（其中e是自然对数的底数），若关于x的方程恰有三个不同的零点，且，则的最大值为（ ）
A．B．C．D．
2．（2022·全国·模拟预测）已知函数，实数，是函数的零点，若，则的取值范围为（ ）
A．B．
C．D．
3．（2023·天津南开 ）已知函数若函数有四个零点，且，则的取值范围是（ ）
A．B．C．D．
考法八 嵌套函数的零点
【例8-1】（2023·陕西咸阳·统考模拟预测）已知函数，则函数的零点个数是（ ）
A．B．C．D．
【例8-2】（2023·河南南阳）已知函数，若函数有6个不同的零点，则实数m的范围是（ ）
A．B．C．D．
【变式】
1．（2023·江西赣州·统考一模）若函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
2．（2023·全国·学军中学校联考二模）已知函数（为自然对数的底数），则函数的零点个数为（ ）
A．3B．5C．7D．9
3．（2023·陕西西安）已知函数是定义域为的偶函数，当时，，若关于的方程有且仅有8个不同的实数根，则实数的取值范围是（ ）.
A．B．C．D．
4．（2022·四川宜宾·校考三模）已知函数，要使函数的零点个数最多，则k的取值范围是
A．B．
C．D．
1．（2023·海南·模拟预测）函数的零点所在的大致区间为（ ）
A．B．C．D．
2．（2023·云南昭通·校考模拟预测）函数的零点所在的区间是（ ）
A．B．C．D．
3．（2023·重庆酉阳·重庆市酉阳第一中学校校考一模）函数的零点所在的区间是（ ）
A．B．C．D．
4．（2023·江苏扬州·江苏省高邮中学校考模拟预测）已知函数 在 上单调递增，则f（x）在上的零点可能有（ ）
A．2个B．3个C．4个D．5个
5．（2023·山东潍坊·统考模拟预测）函数在区间上的零点个数是（ ）
A．3B．4C．5D．6
6．（2023·四川凉山·二模）已知是定义域为的偶函数且，则函数零点个数是（ ）
A．6B．5C．4D．3
7．（2023·江西赣州·统考一模）若函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
8．（2023·江西赣州·统考一模）已知函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
9．（2023·陕西咸阳·统考一模）已知定义在上的偶函数满足：当时，，且，则方程实根个数为（ ）
A．6B．8C．9D．10
10．（2022·陕西西安·长安一中校考模拟预测）已知函数，，的零点分别为、、，则、、的大小顺序为（ ）
A．B．
C．D．
11．（2022·河北石家庄·统考模拟预测）若，则下列不等关系一定不成立的是（ ）
A．B．C．D．
12．（2022·陕西西安·统考模拟预测）已知函数，，的零点依次为，则以下排列正确的是（ ）
A．B．
C．D．
13．（2023·上海嘉定·校考三模）已知函数，若满足（、、互不相等），则的取值范围是（ ）
A．B．C．D．
14．（2023·河南·统考三模）已知函数是定义域为的偶函数，且满足，当时，，则关于的方程在上所有实数解之和为（ ）
A．9B．C．D．7
15．（2022·江西·江西师大附中校考三模）定义在R上的函数满足，且当时，.则函数的所有零点之和为（ ）
A．7B．14C．21D．28
16．（2022·全国·模拟预测）已知函数，实数，是函数的零点，若，则的取值范围为（ ）
A．B．
C．D．
17．（2022·江西新余·新余市第一中学校考模拟预测）已知定义在上的奇函数，满足，且当时，，若方程在区间上有四个不同的根、、、，则的值为（ ）
A．B．C．D．
18．（2024东济宁）已知函数，若，则的最小值是（ ）
A．B．C．D．
19．（2023·江西宜春）已知函数，若方程有四个不同的解，，，，且，则的取值范围是（ ）
A．B．C．D．
20．（2023·江西宜春·江西省丰城拖船中学校考一模）已知定义在R上的函数满足，且，若关于x的方程恰有5个不同的实数根，则的取值范围是（ ）
A．B．C．D．
21．（2023·天津 ）已知函数关于的方程，.有四个不同的实数解，，，，则的取值范围为（ ）
A．B．C．D．
22．（2023·海淀 ）设函数若关于的方程有四个实数解，其中，则的取值范围是（ ）
A．B．C．D．
23（多选）．（2023·山东菏泽）已知，分别是函数和的零点，则（ ）
A．B．C．
D．
24．（2023·全国·统考高考真题）已知函数在区间有且仅有3个零点，则的取值范围是 ．
25（2022·天津·统考高考真题）设，对任意实数x，记．若至少有3个零点，则实数的取值范围为 .
26．（2023·山西·校联考模拟预测）已知函数有3个零点，则实数a的取值范围为 ．
27（2023·安徽滁州·校考模拟预测）已知函数在区间上有零点，则实数m的取值范围是 ．
28．（2023·广西梧州·校考一模）若函数在区间内恰有一个零点，则实数a的取值范围是 ．
29．（2023·浙江·二模）已知函数，则至多有 个实数解.
30．（2023·甘肃武威·统考三模）已知函数满足：当时，，且对任意都成立，则方程的实根个数是 ．
31（2023·全国·模拟预测）已知则函数的零点个数是 ．
32．（2023·陕西咸阳·武功县普集高级中学统考一模）已知函数，则函数零点的个数是 ．
33．（2022·内蒙古呼和浩特·统考二模）若，，，则x、y、z由小到大的顺序是 .
34．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）对于函数，若关于x的方程恰有3个不同的实根,,，则 .
35．（2023·湖南长沙·雅礼中学校考模拟预测）已知函数的定义域为，且，函数在区间内的所有零点为（i=1，2，3，…，n）．若，则实数a的取值范围是 ．
36．（2023·全国·校联考三模）已知函数的部分图象如图所示，同时满足，若函数在区间上共有8个零点，则这8个零点之和为 .
37．（2023·广东·统考一模）已知是定义在上的奇函数，且在上单调递减，为偶函数，若在上恰好有4个不同的实数根，则 .
38．（2023·福建宁德·福鼎市第一中学校考模拟预测）已知的定义域为,且是奇函数,当时,,.函数,则方程的所有的根之和为 .
39．（2022·甘肃兰州·统考模拟预测）函数有三个零点，且，则的取值范围是 ．
40．（2023·天津河北·统考二模）已知函数，若存在实数.满足，且，则 ，的取值范围是 .
专题06 零点（选填题8种考法）
考法一 零点区间
【例1】（2023·吉林长春·东北师大附中校考一模）方程的根所在区间是（ ）
A．B．C．D．
【答案】B
【解析】设，则方程根所在区间即为零点所在区间，
与在上均为增函数，在上单调递增；
对于A，，当时，，A错误；
对于B，，，即，
，使得，B正确；
对于CD，当时，，在区间和上无零点，C错误，D错误.
故选：B.
【变式】
1．（2023·海南·模拟预测）函数的零点所在的大致区间为（ ）
A．B．C．D．
【答案】C
【解析】在连续不断，且单调递减，
，
所以零点位于，故选：C
2．（2023·云南昆明·昆明一中校考模拟预测）函数的零点所在的区间为（ ）
A．B．
C．D．
【答案】C
【解析】在上单调递增，在上单调递增，
函数在上单调递增，
∵，
，
，
函数的零点所在的区间为.
故选：C
3．（2023·广东梅州·统考二模）用二分法求方程近似解时，所取的第一个区间可以是（ ）
A．B．C．D．
【答案】B
【解析】令，
因为函数在上都是增函数，
所以函数在上是增函数，
，
所以函数在区间上有唯一零点，
所以用二分法求方程近似解时，所取的第一个区间可以是.
故选：B.
考法二 零点区间求参数
【例2-1】（2023·宁夏银川·银川一中校考三模）函数在区间上存在零点，则实数的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】由零点存在定理可知，若函数在区间上存在零点，
显然函数为增函数，只需满足，即，
解得，所以实数的取值范围是.
故选：D
【例2-2】（2023·浙江绍兴·统考二模）已知函数，若在区间上有零点，则的最大值为 .
【答案】
【解析】设，则，
此时，则，
令，
当时，，
记，则，
所以在上递增，在上递减，
故,所以，
所以的最大值为.
故答案为：.
【变式】
1．（2023·北京·统考模拟预测）已知函数，若方程的实根在区间上，则k的最大值是（ ）
A．B．C．D．
【答案】C
【解析】当时，，当时，解得；
当时，，其中，，
当时，解得，综上k的最大值是1.
故选：C.
2．（2023·安徽滁州·校考模拟预测）已知函数在区间上有零点，则实数m的取值范围是________．
【答案】
【解析】因为与在上都单调递增，
所以在上单调递增，
因为在区间上有零点，
所以，即，即，解得，
所以实数m的取值范围为.故答案为：.
3．（2023·吉林通化·梅河口市第五中学校考模拟预测）已知函数在区间上存在零点，则的最小值为 .
【答案】
【解析】设函数的零点为，则，则点在直线上.
因为表示与的距离，所以则的最小值即为原点到直线的距离的最小值平方，即，
令，
令，当时，单调递增，
当时，单调递减，所以当时，，
所以的最小值为.
故答案为：
考法三 判断零点个数
【例3-1】（2023·河南·校联考模拟预测）函数的零点个数为（ ）
A．0B．1C．2D．3
【答案】B
【解析】由，得，因此函数的零点即为函数与的图象交点横坐标，在同一坐标系内作出函数与的图象，如图，

观察图象知，函数与的图象有唯一公共点，
所以函数的零点个数为1.故选：B
【例3-2】．（2023·贵州黔东南·凯里一中校考模拟预测）函数在内零点的个数为（ ）
A．1B．2C．3D．4
【答案】C
【解析】由，得，
由，得或或，
则或或
所以在内零点的个数为3.
故选：C.
【例3-3】（2023·河南·校联考模拟预测）设是定义在上的周期为5的奇函数，，则在内的零点个数最少是（ ）
A．4B．6C．7D．9
【答案】D
【解析】因为是定义在上的周期为5的奇函数，
所以，又，所以，
则，则．
所以，
故零点至少有，则在内的零点个数最少是9．
故选：D
【变式】
1．（2023·山东潍坊·统考模拟预测）函数在区间上的零点个数是（ ）
A．3B．4C．5D．6
【答案】A
【解析】求函数在区间上的零点个数，
转化为方程在区间上的根的个数.
由，得或，
解得：或或，
所以函数在区间上的零点个数为3.
故选：A.
2．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知方程的解个数为（ ）
A．0B．1C．2D．3
【答案】C
【解析】易知不是方程的解，所以方程等价于，
构造函数，
，
所以在上单调递增，
又，
所以方程在区间上有且仅有一个解，
，
所以方程在区间上有且仅有一个解，
所以方程的解的个数为，即方程的解个数为.
故选：C.
3．（2023·江苏扬州·江苏省高邮中学校考模拟预测）已知函数 在 上单调递增，则f（x）在上的零点可能有（ ）
A．2个B．3个C．4个D．5个
【答案】A
【解析】由，，即只能取0，得 ，
因为在 上单调递增，则 解得，
由 ，则 ，设，
则 ，因为，，
所以函数在 上的零点最多有2个；
故选：A.
4．（2023·宁夏银川·统考模拟预测）是定义在上的奇函数，当时，，，令，则函数的零点个数为（ ）
A．4B．5C．6D．7
【答案】B
【解析】由可得，的图象关于对称，
又由可得，
所以，所以以4为周期，
所以作出的图象如下，
的零点个数即为方程的根的个数，
也即的图象与图象的交点个数，
因为，
所以数形结合可得的图象与图象的交点个数为5个，
故选:B.
5．（2023·江西上饶·统考一模）已知函数，则在上的零点个数是（ ）
A．2023B．2024C．2025D．2026
【答案】B
【解析】因为，
所以函数是周期为的周期函数，
又，
当时，令，
可得或或
当时，，当且仅当时，
函数在上单调递增，
因为，，所以函数在存在一个零点；
当时，，当且仅当时，，
所以函数在上单调递减，
因为，，
所以函数在存在一个零点；
当时，，所以函数在上单调递增，
因为，，
所以函数在不存在零点；
所以当时，函数有两个零点，且零点位于区间内，
所以在上共有个零点.
故选：B.
考法四 根据零点个数求参数
【例4-1】（2023·全国·统考高考真题）已知函数在区间有且仅有3个零点，则的取值范围是 ．
【答案】
【解析】因为，所以，
令，则有3个根，
令，则有3个根，其中，
结合余弦函数的图像性质可得，故，
故答案为：.
【例4-2】（2022·天津·统考高考真题）设，对任意实数x，记．若至少有3个零点，则实数的取值范围为 .
【答案】
【解析】设，，由可得.
要使得函数至少有个零点，则函数至少有一个零点，则，
解得或.
①当时，，作出函数、的图象如下图所示：
此时函数只有两个零点，不合乎题意；
②当时，设函数的两个零点分别为、，
要使得函数至少有个零点，则，
所以，，解得；
③当时，，作出函数、的图象如下图所示：
由图可知，函数的零点个数为，合乎题意；
④当时，设函数的两个零点分别为、，
要使得函数至少有个零点，则，
可得，解得，此时.
综上所述，实数的取值范围是.
故答案为：.
【变式】
1．（2023·广西梧州·校考一模）若函数在区间内恰有一个零点，则实数a的取值范围是 ．
【答案】
【解析】当时，，符合题意，
当时，二次函数的判别式为：，
若，此时函数的零点为，符合题意；
当时，只需，所以且；
当时，，经验证符合题意；当时，，经验证符合题意；
所以实数a的取值范围为.
故答案为：
2．（2023·江苏淮安·江苏省郑梁梅高级中学校考模拟预测）已知函数有三个零点，则a的取值范围是______.
【答案】
【解析】由得，，
所以若函数有三个零点，则方程有三个根，
设，则，
令得，或，
当时，，递减，
当时，，递增，
当时，，递减，
又，
作出函数的大致图像，如图，
由图可知，当时，函数有三个零点.

故答案为：.
3（2023春·湖北）设函数 在区间[上有零点，则实数的取值范围是___________.
【答案】
【解析】令 ，则，函数 在区间[，3]上有零点等价于直线与曲线在上有交点，
则 ，当时，单调递减，当 时，单调递增，
， ，显然， ，
即当时，函数在上有零点；
故答案为： .
4．（2023·山西·校联考模拟预测）已知函数有3个零点，则实数a的取值范围为 ．
【答案】
【解析】设，则，
设，则，
设，则，
当时，，当时，，
所以在上单调递减，在上单调递增，
则，
①当时，，则，
所以在上单调递增，
所以在上至多一个零点，
所以至多有一个零点，不符合题意；
②当时，，
令，（），
则，
所以在上单调递增，
所以，
所以，
所以，
又因为， ，，
所以由零点存在性定理可知，存在，使得；存在，使得，
所以当时，，当时，，当时，，
所以在上单调递增，在上单调递减，在上单调递增．
又因为，
，，，，
令（），则，
所以在上单调递减，
所以，
所以，
所以，
所以由零点存在性定理知，在，，上各有一个零点，
所以当时，在，，上各有一个零点，
即：当时，在，，上各有一个零点.
所以实数a的取值范围为.
故答案为：.
考法五 比较零点的大小
【例5-1】（2022·安徽合肥·合肥市第六中学校考模拟预测）已知函数，，的零点分别为a，b，c则a，b，c的大小顺序为（ ）
A．B．
C．D．
【答案】D
【解析】由得，，
由得，由得.
在同一平面直角坐标系中画出、、的图象，
由图象知，，.
故选：D
【例5-2】（2023·江西南昌）已知函数，，的零点分别为，，，则（ ）．
A．B．
C．D．
【答案】C
【解析】函数，，的零点，即为与，，的交点，
作出与，，的图象，

如图所示，可知
故选：C
【变式】
1．（2022·重庆沙坪坝·重庆南开中学校考模拟预测）已知实数a，b，c满足，则下列不等式一定不成立的为（ ）
A．B．C．D．
【答案】C
【解析】由的图象如下：
由图知：当时，，D可能；
当时，，B可能；
当时，，A可能.
故选：C
2．（2022·江西·校联考模拟预测）已知函数，，的零点分别是a，b，c，则a，b，c的大小顺序是（ ）
A．B．C．D．
【答案】C
【解析】由已知条件得
的零点可以看成与的交点的横坐标，的零点可以看成与的交点的横坐标，的零点可以看成与的交点的横坐标，
在同一坐标系分别画出，，，的函数图象，如下图所示,
可知，
故选：.
3．（2023·陕西西安）已知函数，，的零点分别为、、，则、、的大小顺序为（ ）
A．B．
C．D．
【答案】A
【解析】因为函数、均为上的增函数，故函数为上的增函数，
因为，，所以，，
因为函数、在上均为增函数，故函数在上为增函数，
因为，，所以，，
由可得，因此，.
故选：A.
考法六 零点之和
【例6-1】（2023·青海西宁·统考二模）函数的所有零点之和为（ ）
A．4B．5C．6D．7
【答案】C
【解析】令，得，解得或，即为零点，
令，，
的周期，对称轴，且的对称轴，
做出和的图象如图所示：
显然，在和上各存在一个零点，
，，在(4,5)上两函数必存在一个交点，
在上有两个零点，同理在上存在两个零点，
所以在上存在6个零点，
因为和关于对称，则零点关于对称，
所以的所有零点之和为.
故选：C
【例6-2】（2023·河南·模拟预测）已知定义域为的函数满足，且曲线与曲线有且只有两个交点，则函数的零点之和是（ ）
A．2B．－2C．4D．－4
【答案】A
【解析】由题意定义域为的函数满足，
则的图象关于点成中心对称，
函数的图象是由的图象向右平移一个单位得到，
故的图象关于点成中心对称，
又曲线与曲线有且只有两个交点，
则这两个交点关于对称，故这两个交点的横坐标之和为2，
而函数的零点即为曲线与曲线交点的横坐标，
故函数的零点之和是2，
故选：A
【变式】
1．（2023·河南·统考三模）已知函数是定义域为的偶函数，且满足，当时，，则关于的方程在上所有实数解之和为（ ）
A．9B．C．D．7
【答案】B
【解析】函数是定义域为的偶函数，当时，，则当时，，
又，则函数的周期是3，显然，
即直线是图象的一条对称轴，因此直线是图象的对称轴，
函数的最小正周期是，直线是图象的对称轴，
函数与在当时取得相同最大值，
在同一坐标平面内作出函数与的图象，如图，
观察图象知，函数与在上有7个公共点，对应横坐标依次为，
由对称性知，，于是，
所以关于的方程在上所有实数解之和为.
故选：B
2．（2022·江西·江西师大附中校考三模）定义在R上的函数满足，且当时，.则函数的所有零点之和为（ ）
A．7B．14C．21D．28
【答案】B
【解析】依题意，是奇函数.又由知，的图像关于对称.
，
所以是周期为4的周期函数.
，
所以关于点对称.
由于
从而函数的所有零点之和即为函数与的图像的交点的横坐标之和.
而函数的图像也关于点对称.
画出，的图象如图所示.由图可知，共有7个交点，所以函数所有零点和为.
故选：B
3．（2023·湖北·校联考模拟预测）函数是定义在R上的奇函数，当时，，则函数在上的所有零点之和为（ ）
A．－32B．32C．16D．8
【答案】D
【解析】函数是定义在R上的奇函数,.
又函数,
函数是偶函数,
函数的零点都是以相反数的形式成对出现的.
函数在上所有的零点的和为,
函数在上所有的零点的和,即函数在上所有的零点之和.
即方程在上的所有实数解之和.
由时,,故有
函数在上的值域为,当且仅当时,.
又当时,,如图：
函数在上的值域为；
函数在上的值域为；
函数在上的值域为,当且仅当时,,
即方程在上的又一个实数解.即有一个零点；
函数在上的值域为,当且仅当时,,
故在上恒成立,在上无零点,
同理在上无零点,
依此类推,函数在无零点.
综上函数在上的所有零点之和为8,
故选：D.
4．（2023·全国·模拟预测）已知定义在上的函数满足：为偶函数，且；函数，则当时，函数的所有零点之和为（ ）
A．B．C．D．
【答案】A
【解析】因为为偶函数，所以关于对称，
所以当时，，
当时，，，
当时，，，
当时，，，
当时，，，
……
函数为的图象向左平移个单位，
的图象如下图所示，
均关于对称，有14个交点，
所以函数的所有零点之和为：.故选：A.
考法七 零点之和的范围
【例7-1】（2023·上海嘉定·校考三模）已知函数，若满足（、、互不相等），则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】作出函数的图象，如图所示：

不妨设，
因为，
由函数的性质得，，即，
所以，
故选：D
【例7-2】．（2023·山东济宁·统考二模）已知函数，若，则的最小值是（ ）
A．B．C．D．
【答案】C
【解析】
函数的图像如图所示，作出交两点，其横坐标分别为a、b，不妨设.
由可得：，解得：，
所以
记，
任取，则。
因为，所以，所以，
所以
则在上单调递减，所以
故选：C
【变式】
1．（2023·吉林长春·东北师大附中校考模拟预测）已知函数，（其中e是自然对数的底数），若关于x的方程恰有三个不同的零点，且，则的最大值为（ ）
A．B．C．D．
【答案】A
【解析】由解析式，在上单调递增且值域为，在上单调递增且值域为，
函数图象如下：
所以，的值域在上任意函数值都有两个x值与之对应，值域在上任意函数值都有一个x值与之对应，要使恰有三个不同的零点，则曲线与直线的交点横坐标一个在上，另一个在上，由开口向下且对称轴为，
由上图知：，此时且，，
结合图象及有，，则，
所以，且，
令且，则，
当时，递增；当时，递减；
所以，故最大值为.
故选：A
2．（2022·全国·模拟预测）已知函数，实数，是函数的零点，若，则的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】由题意，作出直线和函数的大致图象如图所示，
易得，
且，（易错：注意，的范围不是）
由，即，
得，则，
所以，
令，则，，
所以.
因为在上单调递减函数，所以.
即.故选：D
3．（2023·天津南开 ）已知函数若函数有四个零点，且，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】函数有四个零点，即方程有四个根.
作出函数的图像如图.
根据函数图像，方程有四个根，则
，则
，则
所以
由对勾函数在上单调递减，所以，当时等号成立
则的取值范围是
故选：B
考法八 嵌套函数的零点
【例8-1】（2023·陕西咸阳·统考模拟预测）已知函数，则函数的零点个数是（ ）
A．B．C．D．
【答案】A
【解析】函数，
对，令，令，
可知在上单调递增，在上单调递减，
且趋向负无穷时，，时，，
故结合对数函数图象，可画出函数图像如下图所示：
函数的零点，即，令，代入可得，
由图像可知，即，
结合函数图像可知，有1个解，
综合可知，函数的零点有1个，
故选：A.
【例8-2】（2023·河南南阳）已知函数，若函数有6个不同的零点，则实数m的范围是（ ）
A．B．C．D．
【答案】D
【解析】令，则原函数等价为．
做出函数的图象如图，

图象可知
当时，函数有一个零点．
当时，函数有三个零点．
当时，函数有四个零点．
当时，函数有三个零点．
当时，函数有两个零点．
要使关于的函数有6个不同的零点，
则函数有两个根，，
且，或，，
令，则由根的分布可得，
将，代入得：，
此时的另一个根为，不满足，，
若，，则，
解得：，
故答案为：．
故选：D﹒
【变式】
1．（2023·江西赣州·统考一模）若函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
【答案】A
【解析】由，
则可作出函数的图象如下：
由方程，得或，
所以方程的实根个数为3．
故选：A．
2．（2023·全国·学军中学校联考二模）已知函数（为自然对数的底数），则函数的零点个数为（ ）
A．3B．5C．7D．9
【答案】C
【解析】设，令可得：,
对于，，故在处切线的斜率值为，
设与相切于点，
切线斜率，则切线方程为：，
即，解得：；
由于，故作出与图象如下图所示，
与有四个不同交点，
即与有四个不同交点，
设三个交点为，由图象可知：，
作出函数的图象如图，
由此可知与无交点，与有三个不同交点，与各有两个不同交点，
的零点个数为7个，
故选：C
3．（2023·陕西西安）已知函数是定义域为的偶函数，当时，，若关于的方程有且仅有8个不同的实数根，则实数的取值范围是（ ）.
A．B．C．D．
【答案】A
【解析】令，因为是定义域为的偶函数，画出的图象如下：
由图象可知：当时，有4个根，
要想有且仅有8个不同的实数根，
则要有两个不相等的实数根，且，
令，
则，解得：.
故选：A
4．（2022·四川宜宾·校考三模）已知函数，要使函数的零点个数最多，则k的取值范围是
A．B．
C．D．
【答案】B
【解析】因为，所以，
可得在上递减，在递增，
所以，有最小值，且时，，当x趋向于负无穷时，f(x)趋向于0，但始终小于0，所以，时，最多有两个根，
最多有2个根，
即在有两个根时，
的零点最多为4个，
，解得，故选B.
1．（2023·海南·模拟预测）函数的零点所在的大致区间为（ ）
A．B．C．D．
【答案】C
【解析】在连续不断，且单调递减，
，
所以零点位于，
故选：C
2．（2023·云南昭通·校考模拟预测）函数的零点所在的区间是（ ）
A．B．C．D．
【答案】B
【解析】易知为增函数，又，
，故零点所在的区间是.
故选：B.
3．（2023·重庆酉阳·重庆市酉阳第一中学校校考一模）函数的零点所在的区间是（ ）
A．B．C．D．
【答案】D
【解析】函数，画出与的图象，如下图：
当时，，
当时，，
函数的零点所在的区间是．
故选：D．
4．（2023·江苏扬州·江苏省高邮中学校考模拟预测）已知函数 在 上单调递增，则f（x）在上的零点可能有（ ）
A．2个B．3个C．4个D．5个
【答案】A
【解析】由，，即只能取0，得 ，
因为在 上单调递增，则 解得，
由 ，则 ，设，
则 ，因为，，
所以函数在 上的零点最多有2个；
故选：A.
5．（2023·山东潍坊·统考模拟预测）函数在区间上的零点个数是（ ）
A．3B．4C．5D．6
【答案】A
【解析】求函数在区间上的零点个数，
转化为方程在区间上的根的个数.
由，得或，
解得：或或，
所以函数在区间上的零点个数为3.
故选：A.
6．（2023·四川凉山·二模）已知是定义域为的偶函数且，则函数零点个数是（ ）
A．6B．5C．4D．3
【答案】A
【解析】时，，
当时，，，
当时，，，
，有；，有，
所以在上单调递减，在上单调递增，在上单调递减，
，，，，
，，，
由零点存在定理，所以在，，上各有一个零点，
又是定义域为的偶函数，则函数有6个零点.
故选：A
7．（2023·江西赣州·统考一模）若函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
【答案】A
【解析】由，
则可作出函数的图象如下：
由方程，得或，
所以方程的实根个数为3．
故选：A．
8．（2023·江西赣州·统考一模）已知函数，则方程的实根个数为（ ）
A．3B．4C．5D．6
【答案】A
【解析】，解得或，
当时，，解得，，解得（舍）；
当时，，解得或（舍），，解得或（舍）；
综上，方程的实根为或或，
即方程的实根个数为3个，
故选：A.
9．（2023·陕西咸阳·统考一模）已知定义在上的偶函数满足：当时，，且，则方程实根个数为（ ）
A．6B．8C．9D．10
【答案】B
【解析】因为函数满足，
所以，，即函数为周期函数，周期为，
因为当时，，
所以，当时，恒成立，
所以，函数在上单调递增，
因为为定义在上的偶函数，
令，则定义域为，，
所以函数为定义在上的偶函数，
因为
因为，
所以
所以，作出函数，图象如图，
由图象可知，当时，函数与图象有4个交点，
所以，由偶函数的对称性可知，当时，函数与图象有4个交点，
所以，方程实根个数为个.
故选：B
10．（2022·陕西西安·长安一中校考模拟预测）已知函数，，的零点分别为、、，则、、的大小顺序为（ ）
A．B．
C．D．
【答案】A
【解析】因为函数、均为上的增函数，故函数为上的增函数，
因为，，所以，，
因为函数、在上均为增函数，故函数在上为增函数，
因为，，所以，，
由可得，因此，.
故选：A.
11．（2022·河北石家庄·统考模拟预测）若，则下列不等关系一定不成立的是（ ）
A．B．C．D．
【答案】D
【解析】由，得．
由，得，，
作函数，，的图象，再作直线．
变换m的值发现：，，均能够成立， D不可能成立.
故选：D．
12．（2022·陕西西安·统考模拟预测）已知函数，，的零点依次为，则以下排列正确的是（ ）
A．B．
C．D．
【答案】B
【解析】函数，，的零点依次为，
在同一直角坐标系中画出，，与的图像如图所示，由图可知，，，满足
故选：B．
13．（2023·上海嘉定·校考三模）已知函数，若满足（、、互不相等），则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】作出函数的图象，如图所示：

不妨设，
因为，
由函数的性质得，，即，
所以，
故选：D
14．（2023·河南·统考三模）已知函数是定义域为的偶函数，且满足，当时，，则关于的方程在上所有实数解之和为（ ）
A．9B．C．D．7
【答案】B
【解析】函数是定义域为的偶函数，当时，，则当时，，
又，则函数的周期是3，显然，
即直线是图象的一条对称轴，因此直线是图象的对称轴，
函数的最小正周期是，直线是图象的对称轴，
函数与在当时取得相同最大值，
在同一坐标平面内作出函数与的图象，如图，
观察图象知，函数与在上有7个公共点，对应横坐标依次为，
由对称性知，，于是，
所以关于的方程在上所有实数解之和为.
故选：B
15．（2022·江西·江西师大附中校考三模）定义在R上的函数满足，且当时，.则函数的所有零点之和为（ ）
A．7B．14C．21D．28
【答案】B
【解析】依题意，是奇函数.又由知，的图像关于对称.
，
所以是周期为4的周期函数.
，
所以关于点对称.
由于
从而函数的所有零点之和即为函数与的图像的交点的横坐标之和.
而函数的图像也关于点对称.
画出，的图象如图所示.由图可知，共有7个交点，所以函数所有零点和为.
故选：B
16．（2022·全国·模拟预测）已知函数，实数，是函数的零点，若，则的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】由题意，作出直线和函数的大致图象如图所示，
易得，
且，（易错：注意，的范围不是）
由，即，
得，则，
所以，
令，则，，
所以.
因为在上单调递减函数，所以.
即.
故选：D
17．（2022·江西新余·新余市第一中学校考模拟预测）已知定义在上的奇函数，满足，且当时，，若方程在区间上有四个不同的根、、、，则的值为（ ）
A．B．C．D．
【答案】A
【解析】因为函数为上的奇函数，所以，，故函数的图象关于直线对称，
因为，故函数是周期为的周期函数，
当时，，
因为函数、在上均为增函数，故函数在上也为增函数，、
作出函数和在上的图象如下图所示：
设，由图可知，点与点关于直线对称，
点与点关于直线对称，
因此，.
故选：A.
18．（2024东济宁）已知函数，若，则的最小值是（ ）
A．B．C．D．
【答案】C
【解析】
函数的图像如图所示，作出交两点，其横坐标分别为a、b，不妨设.
由可得：，解得：，
所以
记，
任取，则。
因为，所以，所以，
所以
则在上单调递减，所以
故选：C
19．（2023·江西宜春）已知函数，若方程有四个不同的解，，，，且，则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】方程有四个不同的解等价于与有四个不同的交点，如下图所示：
则与关于对称，，
，，，
令，解得：；令，解得：；
，
在上单调递增，
，
即的取值范围为.
故选：D.
20．（2023·江西宜春·江西省丰城拖船中学校考一模）已知定义在R上的函数满足，且，若关于x的方程恰有5个不同的实数根，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】 ，是奇函数，的函数图象关于原点对称.
作出函数的图象如图所示：
由图象可知，设，
根据二次函数的对称性可知：，
.
故选：B.
21．（2023·天津 ）已知函数关于的方程，.有四个不同的实数解，，，，则的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】 作函数的图象如图：
结合图象可知，，
，
故，
根据题意，，
则，
故，
则，
根据对勾函数在上单调递增，
故在上单调递增，
所以，
故选：B.
22．（2023·海淀 ）设函数若关于的方程有四个实数解，其中，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】，画出函数图像，如图所示：
根据图像知：，，故，且.
故.
故选：.
23（多选）．（2023·山东菏泽）已知，分别是函数和的零点，则（ ）
A．B．C．
D．
【答案】BCD
【解析】令，得，即，，
令，得，即，即，，
记函数，，则，
所以函数在上单调递增，
因为，，所以，故A错误；
又，所以，，
所以，故B正确；
所以，故C正确；
又，所以，结合，得，
因为，所以，且，
因为在区间上单调递减，所以，
即，故D正确；
故选：BCD
24．（2023·全国·统考高考真题）已知函数在区间有且仅有3个零点，则的取值范围是 ．
【答案】
【解析】因为，所以，
令，则有3个根，
令，则有3个根，其中，
结合余弦函数的图像性质可得，故，
故答案为：.
25（2022·天津·统考高考真题）设，对任意实数x，记．若至少有3个零点，则实数的取值范围为 .
【答案】
【解析】设，，由可得.
要使得函数至少有个零点，则函数至少有一个零点，则，
解得或.
①当时，，作出函数、的图象如下图所示：
此时函数只有两个零点，不合乎题意；
②当时，设函数的两个零点分别为、，
要使得函数至少有个零点，则，
所以，，解得；
③当时，，作出函数、的图象如下图所示：
由图可知，函数的零点个数为，合乎题意；
④当时，设函数的两个零点分别为、，
要使得函数至少有个零点，则，
可得，解得，此时.
综上所述，实数的取值范围是.
故答案为：.
26．（2023·山西·校联考模拟预测）已知函数有3个零点，则实数a的取值范围为 ．
【答案】
【解析】设，则，
设，则，
设，则，
当时，，当时，，
所以在上单调递减，在上单调递增，
则，
①当时，，则，
所以在上单调递增，
所以在上至多一个零点，
所以至多有一个零点，不符合题意；
②当时，，
令，（），
则，
所以在上单调递增，
所以，
所以，
所以，
又因为， ，，
所以由零点存在性定理可知，存在，使得；存在，使得，
所以当时，，当时，，当时，，
所以在上单调递增，在上单调递减，在上单调递增．
又因为，
，，，，
令（），则，
所以在上单调递减，
所以，
所以，
所以，
所以由零点存在性定理知，在，，上各有一个零点，
所以当时，在，，上各有一个零点，
即：当时，在，，上各有一个零点.
所以实数a的取值范围为.
故答案为：.
27（2023·安徽滁州·校考模拟预测）已知函数在区间上有零点，则实数m的取值范围是 ．
【答案】
【解析】因为与在上都单调递增，
所以在上单调递增，
因为在区间上有零点，
所以，即，即，
解得，
所以实数m的取值范围为.
故答案为：.
28．（2023·广西梧州·校考一模）若函数在区间内恰有一个零点，则实数a的取值范围是 ．
【答案】
【解析】当时，，符合题意，
当时，二次函数的判别式为：，
若，此时函数的零点为，符合题意；
当时，只需，所以且；
当时，，经验证符合题意；当时，，经验证符合题意；
所以实数a的取值范围为.
故答案为：
29．（2023·浙江·二模）已知函数，则至多有 个实数解.
【答案】7
【解析】由可得，由知，，
当时，，，
当时，，在单调递增，
当时，，在单调递减，
当时，，，在单调递增，
则可作出函数的大致图像如图：
三个图分别对应时的情况，
设，则即，
则的解的个数问题即为的交点个数问题，
结合的图象可知的交点个数最多是3个，
即为图2个和图3所示情况，
不妨设交点横坐标为，当如图2所示时，，
此时无解，有1个解，最多有3个解，
故此时最多有4个解；
当如第3个图所示时，，
此时有一个解，最多有3个解，最多有3个解，
故此时最多有7个解；
故答案为：7
30．（2023·甘肃武威·统考三模）已知函数满足：当时，，且对任意都成立，则方程的实根个数是 ．
【答案】4
【解析】依题意，函数是以4为周期的偶函数，当时，，
则当时，，
方程，
因此原方程的实根就是函数与函数的图象的交点的横坐标，
在同一坐标系内作出函数与的图象，如图，
观察图象知，当时，两函数图象只有一个交点，
当时，由得，即当时，两函数图象只有一个公共点，
于是当时，函数与的图象有2个公共点，
又函数与均为偶函数，则当时，两个函数图象有2个公共点，
所以函数与的图象有4个公共点，即原方程有4个根．
故答案为：4
31（2023·全国·模拟预测）已知则函数的零点个数是 ．
【答案】7
【解析】函数的零点即为方程的根，解方程得或．
作出函数的图像，如图所示．
由图像知直线与的图像有4个交点，直线与的图像有3个交点．
因此函数的零点有7个．
故答案为：7
32．（2023·陕西咸阳·武功县普集高级中学统考一模）已知函数，则函数零点的个数是 ．
【答案】
【解析】令，即，解得或，
作出函数的图象如图，
由图可知，方程有个实数解，有个实数解，且均互不相同，
所以，的实数解有个，
所以，函数零点的个数是个.
故答案为：
33．（2022·内蒙古呼和浩特·统考二模）若，，，则x、y、z由小到大的顺序是 .
【答案】
【解析】依题意，，，，，
因此，成立的x值是函数与的图象交点的横坐标，
成立的y值是函数与的图象交点的横坐标，
成立的z值是函数与的图象交点的横坐标，
在同一坐标系内作出函数，的图象，如图，
观察图象得：，即，所以x、y、z由小到大的顺序是.
故答案为：
34．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）对于函数，若关于x的方程恰有3个不同的实根,,，则 .
【答案】/
【解析】由题意，作出函数的图象，如图所示，

若关于x的方程恰有3个不同的实根,,，不妨设，
则，此时，又，则，
所以.
故答案为：.
35．（2023·湖南长沙·雅礼中学校考模拟预测）已知函数的定义域为，且，函数在区间内的所有零点为（i=1，2，3，…，n）．若，则实数a的取值范围是 ．
【答案】
【解析】函数的零点即为函数的图象与函数的图象的交点的横坐标，先作出函数在区间上的图象，
又当时，，所以当时，，
再作出函数的图象，如图所示：

由图象可得：，，，…，，则，
若，得，则实数a的取值范围是.
故答案为：
36．（2023·全国·校联考三模）已知函数的部分图象如图所示，同时满足，若函数在区间上共有8个零点，则这8个零点之和为 .
【答案】
【解析】由题图知.由知，函数的图象关于直线对称.
则由图象可知，解得.
又，所以.所以，最小正周期.所以.
所以.因为函数的图象经过点，
所以，解得.
又，所以，所以.
设方程在上的8个根从小到大依次为.
令，则.根据的图象的对称性，可得.
由的周期性可得
，
所以.
故答案为：.
37．（2023·广东·统考一模）已知是定义在上的奇函数，且在上单调递减，为偶函数，若在上恰好有4个不同的实数根，则 .
【答案】24
【解析】由为偶函数，则，故，
又是定义在上的奇函数，则，
所以，故，即有，
综上，的周期为8，且关于对称的奇函数，
由在上单调递减，结合上述分析知：在上递增，上递减，上递增，
所以在的大致草图如下：
要使在上恰好有4个不同的实数根，即与有4个交点，
所以，必有两对交点分别关于对称，则.
故答案为：24
38．（2023·福建宁德·福鼎市第一中学校考模拟预测）已知的定义域为,且是奇函数,当时,,.函数,则方程的所有的根之和为 .
【答案】5
【解析】解:由题知是奇函数,
则有:,
关于对称,且,
当时,,
,
恒过,且关于对称,
方程的所有的根之和也即是两函数交点的横坐标和,
根据对称性及解析式画出图象如下:
由图像可知,有5个交点,其中一个交点横坐标为1,
另外四个,两两分别关于对称,
故五个交点横坐标和为,
即所有根之和5.
故答案为:5
39．（2022·甘肃兰州·统考模拟预测）函数有三个零点，且，则的取值范围是 ．
【答案】
【解析】设，
因为函数有三个零点，且，
所以的图象与直线交点的横坐标分别为，且，
作出的图象如图所示，
由图可知，且是方程的两个实根，
所以，
因为满足，即，
因为，所以，
所以，
所以，
即的取值范围是，
故答案为：
40．（2023·天津河北·统考二模）已知函数，若存在实数.满足，且，则 ，的取值范围是 .
【答案】 1
【解析】作出函数的图象，如图，

因为，
所以由图可知，，即，，且，
，
在上单调递增，
，
即的取值范围是.
故答案为：1；