
所属成套资源:2024年高考数学二轮复习专题(考法分类新高考版)(原卷版+解析)
2024年高考数学二轮复习专题13空间几何(选填题10种考法)(原卷版+解析)
展开
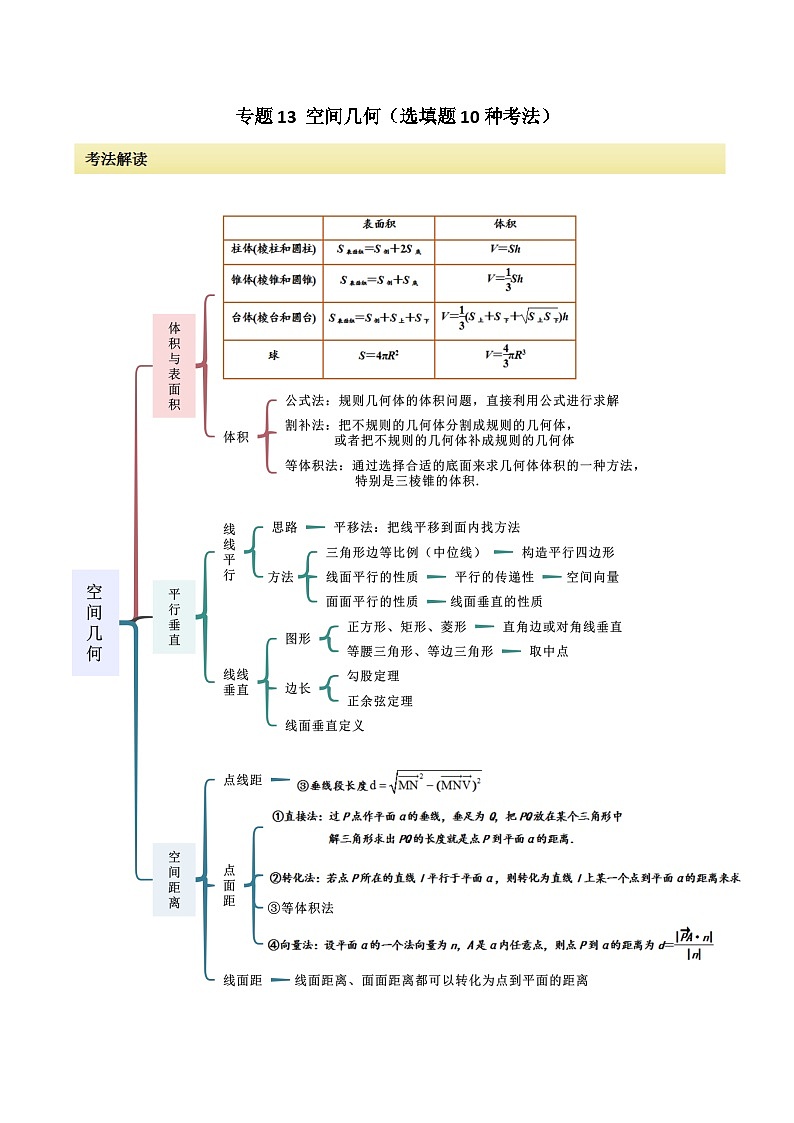
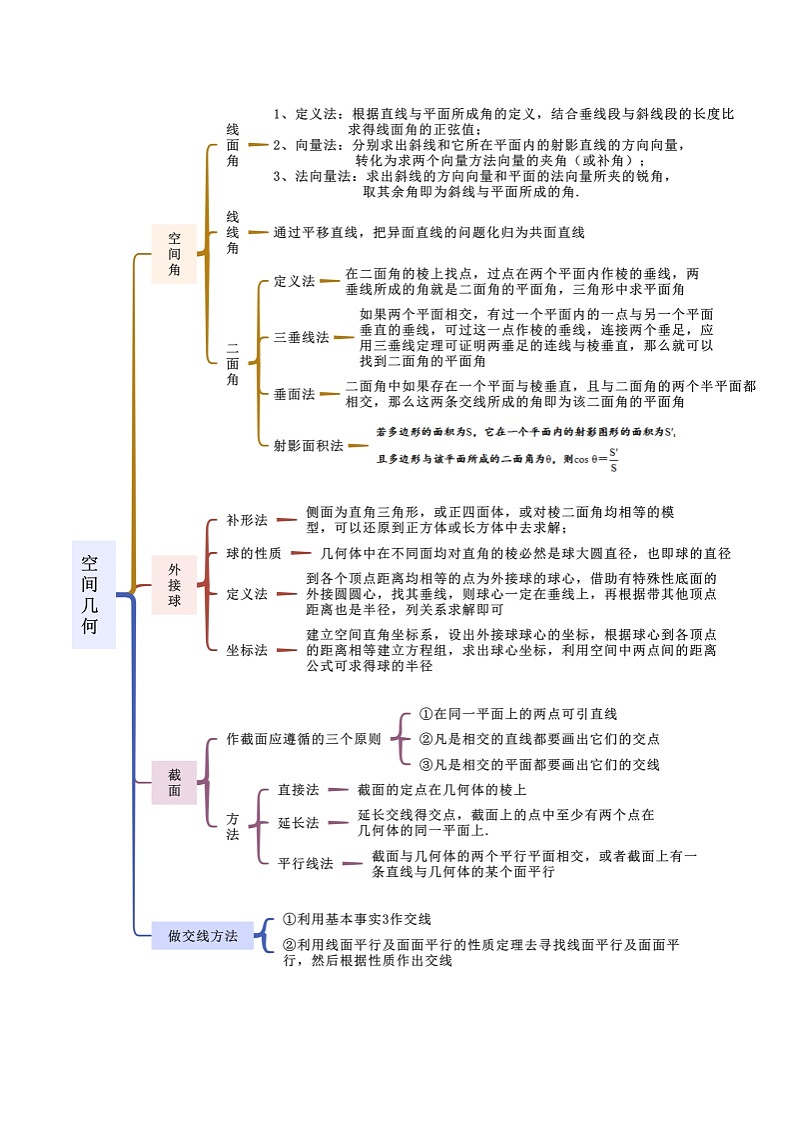
这是一份2024年高考数学二轮复习专题13空间几何(选填题10种考法)(原卷版+解析),共26页。试卷主要包含了空间几何体的体积与表面积,空间几何中的垂直与平行,空间距离,空间角,外接球与内切球,轨迹与轨迹的长度,截面,最值等内容,欢迎下载使用。
考法一 空间几何体的体积与表面积
【例1-1】(2023·全国·统考高考真题)在三棱锥中,是边长为2的等边三角形,,则该棱锥的体积为( )
A.1B.C.2D.3
【例1-2】(2023·全国·统考高考真题)已知四棱锥的底面是边长为4的正方形,,则的面积为( )
A.B.C.D.
【例1-3】(2022·全国·统考高考真题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )
A.B.C.D.
【例1-4】(2023·河南·校联考模拟预测)如图1所示,宫灯又称宫廷花灯,是中国彩灯中富有特色的汉民族传统手工艺品之一.图2是小明为自家设计的一个花灯的直观图,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为和,正六棱台与正六棱柱的高分别为和,则该花灯的表面积为( )
A.B.C.D.
【变式】
1.(2023·全国·统考高考真题)已知圆锥PO的底面半径为,O为底面圆心,PA,PB为圆锥的母线,,若的面积等于,则该圆锥的体积为( )
A.B.C.D.
2.(2023·天津·统考高考真题)在三棱锥中,线段上的点满足,线段上的点满足,则三棱锥和三棱锥的体积之比为( )
A.B.C.D.
3.(2022·天津·统考高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为,腰为3的等腰三角形,则该几何体的体积为( )
A.23B.24C.26D.27
4.(2022·全国·统考高考真题)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为,侧面积分别为和,体积分别为和.若,则( )
A.B.C.D.
考法二 空间几何中的垂直与平行
【例2-1】(2023·江苏连云港·校考模拟预测)设是两条不同的直线,是两个不同的平面,则下列说法正确的是( )
A.若,,则B.若,,则
C.若,,,则D.若,,则
【例2-2】(2022·全国·统考高考真题)在正方体中,E,F分别为的中点,则( )
A.平面平面B.平面平面
C.平面平面D.平面平面
【变式】
1.(2023·福建泉州·统考模拟预测)(多选)已知圆柱的轴截面是正方形,为底面圆的直径,点在圆上,点在圆上,且,不在平面内.若,,,四点共面,则( )
A.直线平面B.直线平面
C.平面平面D.平面平面
2.(2023·全国·模拟预测)(多选)在正方体中,分别是棱的中点,则( )
A.平面B.平面平面
C.平面D.平面平面
3.(2023·福建南平·统考模拟预测)(多选)在棱长为1的正方体中,E,F分别是AB,BC中点,则( )
A.平面
B.平面
C.平面平面
D.点E到平面的距离为
考法三 空间距离
【例3】(2023·陕西西安·西北工业大学附属中学校考模拟预测)在三棱柱中,是棱长为的正四面体,则点到平面的距离为( )
A.B.C.D.
【变式】
1.(2023·河北唐山·统考三模)把边长为的正方形沿对角线折成直二面角,则三棱锥的外接球的球心到平面的距离为( )
A.B.C.D.
2.(2023·四川成都·成都外国语学校校考模拟预测)如图,底面同心的圆锥高为,,在半径为3的底面圆上,,在半径为4的底面圆上,且,,当四边形面积最大时,点到平面的距离为( )
A.B.C.2D.
3.(2020·四川眉山·校考二模)已知正四棱柱ABCD- A1B1C1D1中 ,AB=2,CC1= E为CC1的中点,则直线AC1与平面BED的距离为
A.2B.C.D.1
考法四 空间角
【例4】.(2022·全国·统考高考真题)已知正方体,则( )
A.直线与所成的角为B.直线与所成的角为
C.直线与平面所成的角为D.直线与平面ABCD所成的角为
【变式】
1.(2022·全国·统考高考真题)在长方体中,已知与平面和平面所成的角均为,则( )
A.B.AB与平面所成的角为
C.D.与平面所成的角为
2.(2023·吉林白山·统考二模)已知正四面体,E为的中点,则( ).
A.直线与所成的角为
B.直线与所成的角为
C.直线与平面所成角的余弦值为
D.直线与平面所成角的余弦值为
3.(2023·河北衡水·衡水市第二中学校考三模)(多选)已知正方体,则( )
A.异面直线与所成的角为
B.异面直线与所成角的正切值为
C.直线与平面所成的角为
D.直线与平面所成角的正切值为
考法五 外接球与内切球
【例5-1】(2023·江西九江·统考一模)三棱锥中,与均为边长为的等边三角形,若平面平面,则该三棱锥外接球的表面积为( )
A.B.C.D.
【例5-2】(2023·河北秦皇岛·校联考模拟预测)如图,该几何体为两个底面半径为1,高为1的相同的圆锥形成的组合体,设它的体积为,它的内切球的体积为,则( )
A.B.
C.D.
【变式】
1.(2023·河南·统考模拟预测)在菱形ABCD中,,,AC与BD的交点为G,点M,N分别在线段AD,CD上,且,,将沿MN折叠到,使,则三棱锥的外接球的表面积为 .
2.(2023·四川南充·模拟预测)已知四棱锥的底面是边长为2的正方形,,二面角的余弦值为,则四棱锥的外接球的表面积为 .
3.(2023·四川南充·模拟预测)已知四棱锥的底面是边长为2的正方形,,三棱锥的体积为,则四棱锥的外接球的表面积为 .
考法六 轨迹与轨迹的长度
【例6】(2023·辽宁·校联考模拟预测)如图,将正四面体每条棱三等分,截去顶角所在的小正四面体,余下的多面体就成为一个半正多面体,亦称“阿基米德体”.点A,B,M是该多面体的三个顶点,点N是该多面体表面上的动点,且总满足,若,则该多面体的表面积为 ,点N轨迹的长度为 .
【变式】
1.(2023·江苏南京·校联考一模)如图,在矩形中,,,,,分别为,,,的中点,与交于点,现将,,,分别沿,,,把这个矩形折成一个空间图形,使与重合,与重合,重合后的点分别记为,,为的中点,则多面体的体积为 ;若点是该多面体表面上的动点,满足时,点的轨迹长度为 .
2.(2023春·云南)在棱长为2的正方体中,E为棱BC的中点,F是侧面内的动点,若平面,则点F轨迹的长度为( )
A.B.C.D.
3.(2023·全国·高三专题练习)已知是棱长为1的正方体,点P为正方体表面上任一点,则下列说法不正确的是( )
A.若,则点P的轨迹长度为
B.若,则点P的轨迹长度为
C.若,则点P的迹长度为
D.若,则点P的轨迹长度为
4(2022·全国·高三专题练习)如图,在体积为6的三棱锥中,PA、PB、PC两两互相垂直,,若点M是底面内一动点,且满足,则点M的轨迹长度的最大值为( )
A.6B.3C.D.
考法七 截面
【例7】.(2023·河南·校联考模拟预测)在正四棱柱中,,点分别是,的中点,则过点的平面截正四棱柱所得截面多边形的周长为( )
A.B.C.D.
【变式】
1.(2023·贵州六盘水·统考模拟预测)在正方体中,以点A为球心,棱AB为半径的球将正方体截为P(含球心的部分)和Q两部分,则四边形被球A截得的区域面积与P的表面积之比为 .
2.(2022秋·四川成都·高三成都七中校考阶段练习)已知正四面体的棱长为,为上一点,且,则截面的面积是( )
A.B.C.D.
3.(2022秋·福建福州 )(多选)如图,已知正方体的棱长为1,E为的中点,P为对角线上的一个动点,过P作与平面ACE平行的平面,则此平面截正方体所得的截面( )
A.截面不可能是五边形
B.截面可以是正六边形
C.P从D点向运动时,截面面积先增大后减小
D.截面面积的最大值为
4.(2023·陕西西安·西安市大明宫中学校考模拟预测)在三棱锥中,侧面PAC是等边三角形,底面ABC是等腰直角三角形,,,点M,N,E分别是棱PA,PC,AB的中点,过M,N,E三点的平面截三棱锥所得截面为,给出下列结论:
①截面的形状为正方形;
②截面的面积等于;
③异面直线PA与BC所成角的余弦值为;
④三棱锥外接球的表面积等于.
其中所有正确结论的序号是( )
A.①④B.②③C.①③④D.②③④
考法八 最值
【例8-1】(2022·全国·统考高考真题)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )
A.B.C.D.
【变式】
1.(2022·全国·统考高考真题)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为,且,则该正四棱锥体积的取值范围是( )
A.B.C.D.
2.(2023·河南·校联考模拟预测)在三棱锥中,平面,且,当三棱锥的体积取最大值时,该三棱锥外接球的体积是( )
A.B.C.D.
3.(2023·宁夏石嘴山·统考一模)已知正六棱锥的各顶点都在球的球面上,球心在该正六棱锥的内部,若球的体积为,则该正六棱锥体积的最大值是 .
4.(2023·全国·河南省实验中学校考模拟预测)已知四棱锥的各个顶点都在同一个球面上.若该球的体积为,则该四棱锥体积的最大值是 .
考法九 存在性
【例9】(2023·广西柳州·统考模拟预测)(多选)如图所示的几何体是由正方形沿直线旋转得到的,设是圆弧的中点,是圆弧上的动点(含端点),则( )
A.存在点,使得
B.不存在点,使得
C.存在点,使得平面
D.不存在点,使得直线与平面的所成角为
【变式】
1.(2023·河北秦皇岛·校联考二模)(多选)已知表示空间内两条不同的直线,则使成立的必要不充分条件是( )
A.存在平面,有B.存在平面,有
C.存在直线,有D.存在直线,有
2.(2023·海南·海南中学校考模拟预测)(多选)如图,在矩形中,和交于点,将沿直线翻折,则正确的是( )
A.存在,在翻折过程中存在某个位置,使得
B.存在,在翻折过程中存在某个位置,使得
C.存在,在翻折过程中存在某个位置,使得平面
D.存在,在翻折过程中存在某个位置,使得平面
3.(2022秋·湖北武汉)(多选)如图,已知正方体的棱长为1,点M为棱AB的中点,点P在侧面及其边界上运动,则下列选项中正确的是( )
A.存在点P满足
B.存在点P满足
C.满足的点P的轨迹长度为
D.满足的点P的轨迹长度为
考法十 两点距离与折线段
【例10-1】(2023·山东·沂水县第一中学校联考模拟预测)如图,直三棱柱中,,,,点是的中点,点是线段上一动点,点在平面上移动,则,两点之间距离的最小值为( )
A.B.C.D.1
【例10-2】.(2023·吉林长春·统考模拟预测)已知正方体的棱长为1,点,分别为线段,上的动点,点在平面内,则的最小值是( )
A.B.C.D.
【变式】
1.(2023·江西九江·统考三模)如图,棱长为1的正方体中,P为内一点(包括边界),且线段的长度等于点P到平面ABCD的距离,则线段长度的最小值是( )
A.B.C.D.
2.(2023·陕西宝鸡·校联考模拟预测)如图,长方体中,,,点P是BC的中点,点M是BD1上一动点﹐点N在平面上移动,则MN的最小值为( )
A.2B.3C.4D.5
3.(2023·江西南昌)在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是( )
A.[,]B.[,]C.[,]D.[,]
单选题
1.(2023·河南·校联考模拟预测)圆锥的高为2,其侧面展开图的圆心角为,则该圆锥的体积为( ).
A.B.C.D.
2.(2023·河南郑州·统考模拟预测)《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.意思是一个长方体沿对角面斜解(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为,由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为,,,则下列等式错误的是( )
A.B.
C.D.
3.(2023·陕西商洛·陕西省丹凤中学校考模拟预测)在一个正方体内放置一个最大的圆锥,使圆锥的底面在正方体的底面上,圆锥的顶点在正方体的上底面内,记正方体的体积为,圆锥的体积为,则约为(注:)( )
A.1B.2C.3D.4
4.(2023·海南·统考模拟预测)已知三棱锥的四个顶点都在球的球面上,平面,在底面中,,,若球的体积为,则( )
A.1B.C.D.2
5.(2023·全国·统考高考真题)已知为等腰直角三角形,AB为斜边,为等边三角形,若二面角为,则直线CD与平面ABC所成角的正切值为( )
A.B.C.D.
6.(2022·浙江·统考高考真题)如图,已知正三棱柱,E,F分别是棱上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A.B.C.D.
7.(2022·全国·统考高考真题)已知正三棱台的高为1,上、下底面边长分别为和,其顶点都在同一球面上,则该球的表面积为( )
A.B.C.D.
8.(2022·北京·统考高考真题)已知正三棱锥的六条棱长均为6,S是及其内部的点构成的集合.设集合,则T表示的区域的面积为( )
A.B.C.D.
9.(2023·福建龙岩·统考二模)正方体的棱长为2,若点M在线段上运动,当的周长最小时,三棱锥的外接球表面积为( )
A.B.C.D.
10.(2023·河南·校联考模拟预测)等边的边长为2,D,E分别为AB,AC的中点,将沿DE折起,使点A到达点的位置.若平面平面BCED,则线段的长为( ).
A.B.C.D.
11.(2023·山东·山东省实验中学校考二模)正四棱柱中,,为底面的中心,是棱的中点,正四棱柱的高,点到平面的距离的最大值为( )
A.B.C.D.
12.(2023·广东广州·统考三模)正四棱柱中,,P为上底面的中心,M是棱AB的中点,正四棱柱的高,点M到平面PCD的距离的取值范围是( )
A.B.C.D.
13.(2023·四川广安·统考二模)已知四棱柱的底面是正方形,,,点在底面ABCD的射影为BC中点H,则点到平面ABCD的距离为( )
A.B.C.D.3
14.(2020·四川遂宁·统考二模)用六个完全相同的正方形围成的立体图形叫正六面体.已知正六面体的棱长为,则平面与平面间的距离为( )
A.B.C.D.
15.(2022·青海海东·校考模拟预测)已知在正四面体P-ABC中,D,E,F分别在棱PA,PB,PC上,若PE=4,PF=PD=2,则点P到平面DEF的距离为( )
A.B.C.D.
16.(2022秋·河南洛阳·高三校联考阶段练习)已知三棱锥P-ABC的棱长均为6,且四个顶点均在球心为O的球面上,点E在AB上,,过点E作球O的截面,则截面面积的最小值为( )
A.B.C.D.
二、多选题
17.(2023·全国·统考高考真题)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( )
A.直径为的球体
B.所有棱长均为的四面体
C.底面直径为,高为的圆柱体
D.底面直径为,高为的圆柱体
18.(2023·全国·统考高考真题)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,,,点C在底面圆周上,且二面角为45°,则( ).
A.该圆锥的体积为B.该圆锥的侧面积为
C.D.的面积为
19.(2022·全国·统考高考真题)如图,四边形为正方形,平面,,记三棱锥,,的体积分别为,则( )
A.B.
C.D.
20.(2023·河南·校联考模拟预测)如图,正三棱柱的底面边长为1,高为3,为棱的中点,分别在棱上,且满足取得最小值.记四棱锥、三棱锥的体积分别为,则( )
A.B.C.D.
22.(2023·河北秦皇岛·统考模拟预测)在长方体中,,点在底面的边界及其内部运动,且满足,则下列结论正确的是( )
A.若点满足,则
B.点到平面的距离范围为
C.若点满足,则不存在点使得
D.当时,四面体的外接球体积为
23.(2023·海南省直辖县级单位·嘉积中学校考三模)如图,,是直三棱柱棱上的两个不同的动点,,,则( )
A.平面
B.若为定长,则三棱锥的体积为定值
C.直线与平面所成角等于
D.平面平面.
24.(2023·湖北武汉·华中师大一附中校考模拟预测)已知正方体的棱长为1,M是棱的中点.P是平面上的动点(如图),则下列说法正确的是( )
A.若点P在线段上,则平面
B.平面平面
C.若,则动点P的轨迹为抛物线
D.以的一边所在直线为旋转轴,其余两边旋转一周,在旋转过程中,三棱锥体积的取值范围为
25.(2023·福建厦门·厦门一中校考模拟预测)直三棱柱中,,,点是线段上的动点(不含端点),则( )
A.与不垂直B.平面
C.的最小值为D.的取值范围为
26.(2023·湖南永州·统考一模)菱形的边长为,且,将沿向上翻折得到,使二面角的余弦值为,连接,球与三棱锥的6条棱都相切,下列结论正确的是( )
A.平面
B.球的表面积为
C.球被三棱锥表面截得的截面周长为
D.过点与直线所成角均为的直线可作4条
27.(2023·河北唐山·模拟预测)如图,在三棱台中,表示体积,下列说法正确的是( )
A.
B.成等比数列
C.若该三棱台存在内切球,则
D.若该三棱台存在外接球,则
28.(2023·辽宁沈阳·东北育才学校校考模拟预测)在正方体中,分别为棱上的一点,且,是的中点,是棱上的动点,则( )
A.当时,平面
B.当时,平面
C.当时,存在点,使四点共面
D.当时,存在点,使三条直线交于同一点
29.(2023·云南·云南师大附中校考模拟预测)如图,棱长为的正方体中,点、满足,,其中、,点是正方体表面上一动点,下列说法正确的是( )
A.当时,平面
B.当时,若平面,则的最大值为
C.当时,若,则点的轨迹长度为
D.过、、三点作正方体的截面,截面图形可以为矩形
30.(2023·广东湛江·校考模拟预测)在棱长为1的正方体中,M为底面的中心,,,N为线段AQ的中点,则( )
A.CN与QM共面
B.三棱锥的体积跟的取值无关
C.时,过A,Q,M三点的平面截正方体所得截面的周长为
D.时,
31.(2023·江苏徐州·校考模拟预测)棱长为1的正方体中,点为线段上一点(不包括端点),点为上的动点,下列结论成立的有( )
A.过的截面截正方体所得的截面多边形为等腰梯形
B.的最小值为
C.当点为线段中点时,三棱锥的外接球的半径为
D.两点间的最短距离为
32.(2023·福建厦门·统考模拟预测)如图,在棱长为1的正方体中,点满足,其中,则( )
A.
B.当时,有且仅有一个点,使得平面
C.当时,有且仅有一个点,使得
D.当时,三棱锥的体积为定值
33.(2023·安徽亳州·安徽省亳州市第一中学校考模拟预测)正方体棱长为是直线上的一个动点,则下列结论中正确的是( )
A.的最小值为
B.的最小值为
C.若为直线上一动点,则线段的最小值为
D.当时,过点作三棱锥的外接球的截面,则所得截面面积的最小值为
34.(2023·广东广州·统考二模)已知正四面体的棱长为2,点,分别为和的重心,为线段上一点,则下列结论正确的是( )
A.若取得最小值,则
B.若,则平面
C.若平面,则三棱锥外接球的表面积为
D.直线到平面的距离为
35.(2022秋·山东·高三山东省实验中学校考阶段练习)在正四棱柱中,,,,其中,,则( )
A.存在实数,使得在平面内
B.存在实数,使得平面截该正四棱柱所得到的截面是五边形
C.存在实数,使得平面截该正四棱柱所得到的截面是六边形
D.存在实数,使得直线与该正四棱柱的条棱所在直线所成的角都相等
36.(2022·全国·模拟预测)已知正方体中,,,分别为棱AB,BC的中点,过点E,F作正方体的截面,则下列说法正确的是( )
A.若截面过点,则截面周长为
B.若点是线段上的动点(不含端点),则的最小值为
C.若截面是正六边形,则直线与截面垂直
D.若截面是正六边形,S,T是截面上两个不同的动点,设直线与直线ST所成角的最小值为,则
37.(2022秋·重庆巴南·高三重庆市实验中学校考期中)已知正四棱柱中,,点是线段的中点,点是线段上靠近的三等分点,若正四棱柱被过点,,的平面所截,则所得截面多边形的周长不能为( )
A.B.C.D.
三、填空题
38.(2023春·四川内江·高二四川省资中县第二中学校考开学考试)如图所示,在棱长为3的正方体中,E在棱上,,是侧面上的动点,且平面,则在侧面上的轨迹的长度为 .
39.(2022秋·山西运城·高二山西省运城中学校校联考期中)已知正方体的棱长为1,点M,N是线段上的两个三等分点,动点G在内,且的面积为,则G点的轨迹长度为 .
40.(2022秋·新疆省直辖县级单位·高二新疆石河子一中校考阶段练习)如图,长方体中,,,,点是侧面上的一个动点(含边界),是棱的中点,则下列结论正确的是
①当长度最小时,三棱锥的体积为
②当长度最大时,三棱锥的体积为
③若保持,则点在侧面内运动路径的长度为
④若在平面内运动,且,则点的轨迹为圆弧
41.(2023·山东青岛)如图,在长方体中,,,,、分别为棱、的中点,动点在长方体的表面上,且,则点的轨迹长度为 .
42.(2023·全国·统考高考真题)已知点均在半径为2的球面上,是边长为3的等边三角形,平面,则 .
43.(2023·全国·统考高考真题)在正方体中,为的中点,若该正方体的棱与球的球面有公共点,则球的半径的取值范围是 .
44.(2023·全国·统考高考真题)在正四棱台中,,则该棱台的体积为 .
45.(2023·全国·统考高考真题)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为 .
46.(2023·河北保定·统考二模)如图,在四面体中,,则四面体体积的最大值为 .
47.(2023·河南郑州·统考模拟预测)在四面体中,,,,且,,异面直线,所成的角为,则该四面体外接球的表面积为 .
48.(2023·贵州·校联考模拟预测)如图,在四棱锥中,四边形为矩形,平面,,,该四棱锥的外接球的表面积为 .
49.(2023·海南·统考模拟预测)如图,四棱锥内接于圆柱,为的中点,和为圆柱的两条母线,,四边形为正方形,平面与平面的交线平面,当四棱锥的体积最大时,异面直线与所成角的余弦值为 .
(2023·江西南昌·南昌市八一中学校考三模)已知正四棱柱的每个顶点都在球的球面上,若球的表面积为,则该四棱柱的侧面积的最大值为
相关试卷
这是一份2024年高考数学二轮复习专题05函数性质的综合运用(选填题7种考法)(原卷版+解析),共80页。试卷主要包含了函数的单调性,函数的奇偶性,解不等式,函数性质的综合运用,函数的图像,抽象函数等内容,欢迎下载使用。
这是一份2024年高考数学二轮复习专题04恒成立与存在性求参(选填题6种考法)(原卷版+解析),共52页。试卷主要包含了一元二次不等式在R,一元二次不等式在某区间,等式恒成立或能成立等内容,欢迎下载使用。
这是一份2024年高考数学二轮复习专题03平面向量(选填题10种考法)(原卷版+解析),共92页。试卷主要包含了平面向量的坐标运算,平面向量的基本定理,平面向量的数量积,平面向量的共线定理,平面向量中的取值范围,平面向量与四心,平面向量巧建坐标,平面向量与奔驰定理等内容,欢迎下载使用。









