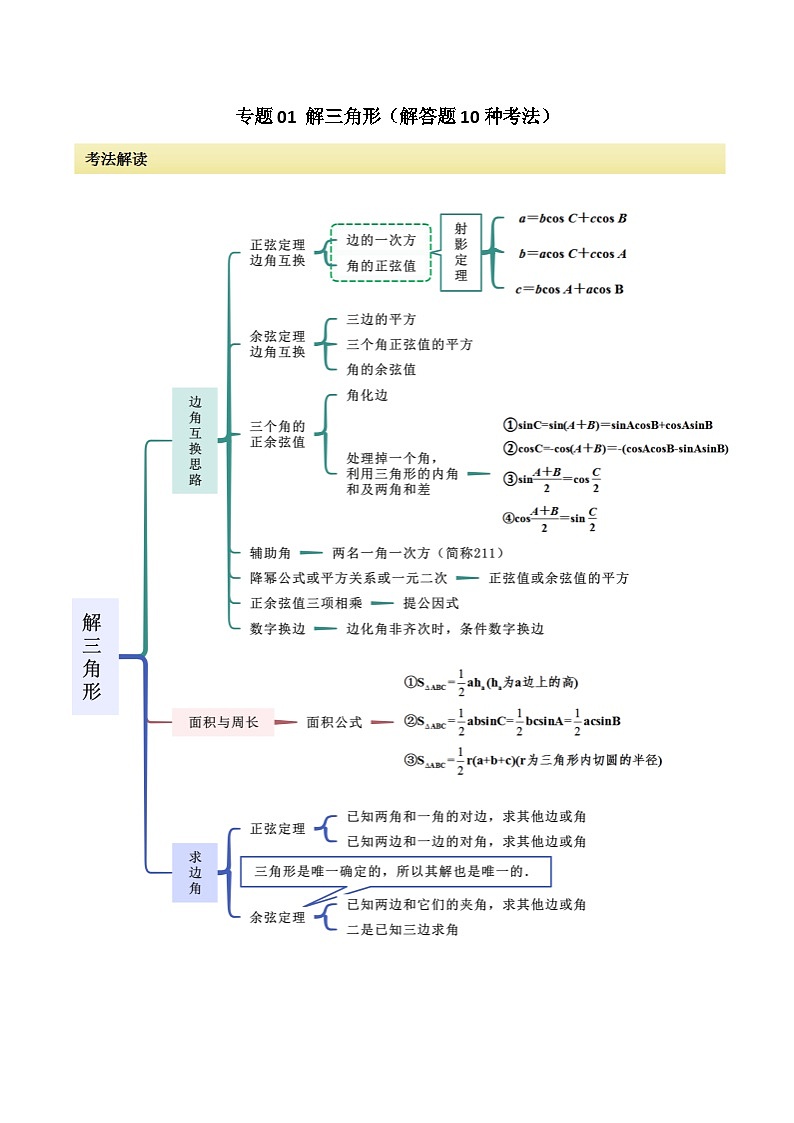
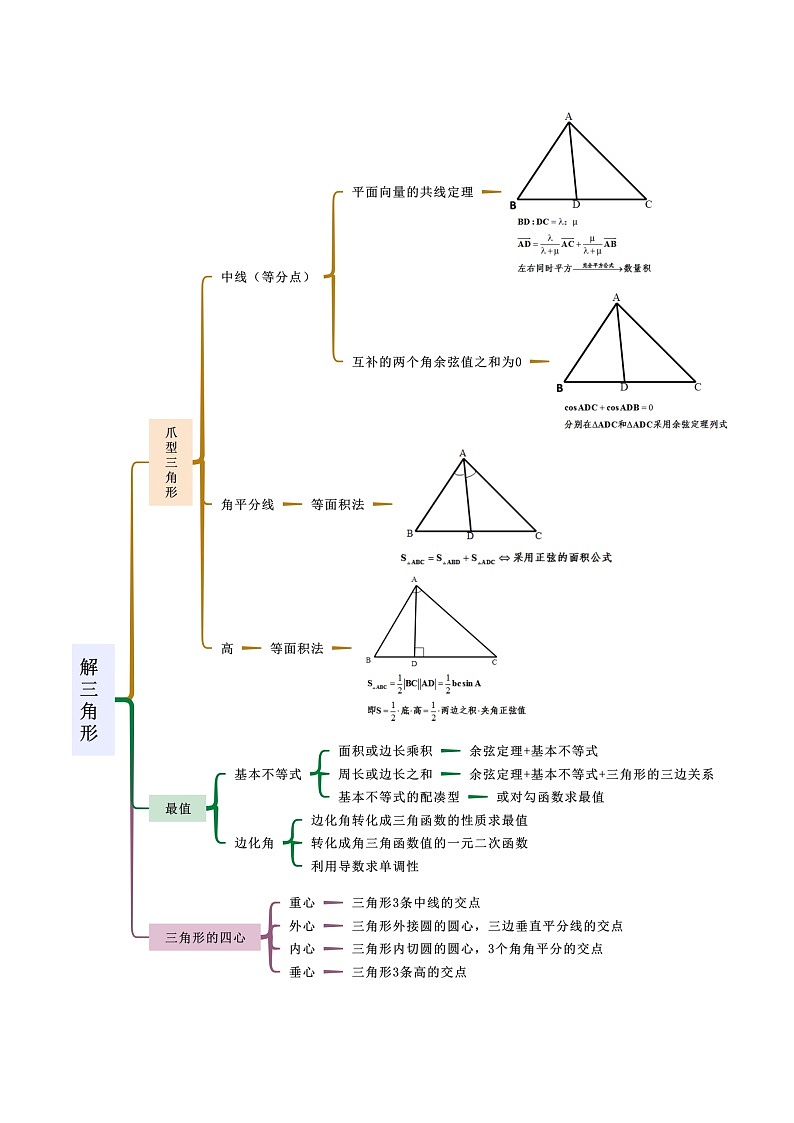
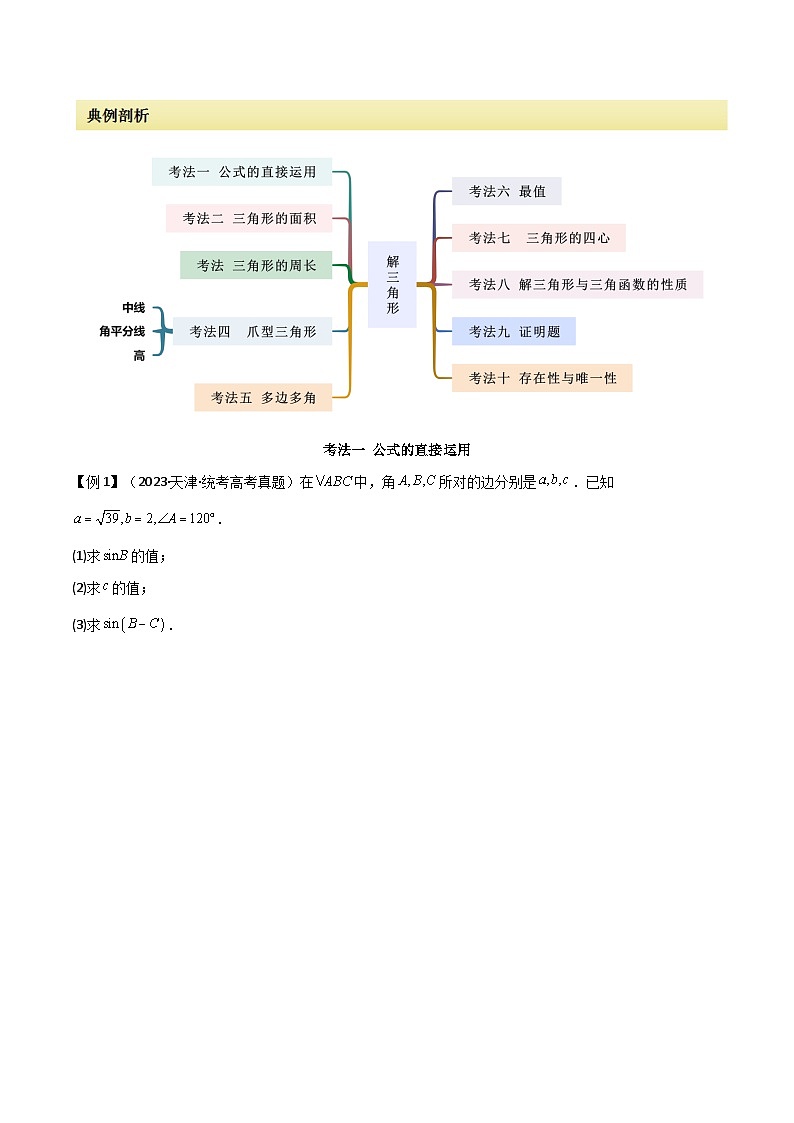
所属成套资源:2024年高考数学二轮复习专题(考法分类新高考版)(原卷版+解析)
2024年高考数学二轮复习专题01解三角形(解答题10种考法)(精讲)(原卷版+解析)
展开
这是一份2024年高考数学二轮复习专题01解三角形(解答题10种考法)(精讲)(原卷版+解析),共76页。试卷主要包含了公式的直接运用,三角形的面积,三角形的周长,多边多角,最值,解三角形与三角函数性质的综合,证明题,存在性与唯一性等内容,欢迎下载使用。
考法一 公式的直接运用
【例1】(2023·天津·统考高考真题)在中,角所对的边分别是.已知.
(1)求的值;
(2)求的值;
(3)求.
【变式】
1.(2022·天津·统考高考真题)在中,角A、B、C的对边分别为a,b,c.已知.
(1)求的值;
(2)求的值;
(3)求的值.
2.(2022·浙江·统考高考真题)在中,角A,B,C所对的边分别为a,b,c.已知.
(1)求的值;
(2)若,求的面积.
3.(2023·天津北辰·校考模拟预测)已知,,分别为锐角三角形三个内角的对边,且.
(1)求;
(2)若,,求;
(3)若,求的值.
考法二 三角形的面积
【例2-1】(2023·福建·校联考模拟预测)设的内角,,的对边分别为,,,已知,,且.
(1)求;
(2)求的面积.
【例2-2】(2023·湖南永州·统考一模)在中,设所对的边分别为,且满足.
(1)求角;
(2)若的内切圆半径,求的面积.
【变式】
1.(2023·海南海口·校考模拟预测)在 中,角 A、B 、C 的对边分别为a 、b 、c ,且满足.
(1)求的值;
(2)若,求的面积.
2.(2023·江苏无锡·校考模拟预测)已知函数.
(1)求函数的最小正周期和单调递增区间;
(2)在中,内角所对的边分别是,且,若,求的面积.
3.(2023·河南开封·统考三模)在中,设A,B,C所对的边分别为a,b,c,且满足.
(1)求角B;
(2)若,的内切圆半径,求的面积.
考法三 三角形的周长
【例3-1】(2023·山东菏泽)在中,角所对的边分别为已知,面积,再从以下两个条件中选择其中一个作为已知,求三角形的周长.
(1);
(2).
注:如果选择多个条件分别解答,按第一个解答计分.
【例3-2】(2023·重庆南岸)设,
(1)求的单调递增区间;
(2)在中,角为锐角,角,,的对边分别为,,,若,,,求三角形的周长.
【变式】
1.(2022·北京·统考高考真题)在中,.
(1)求;
(2)若,且的面积为,求的周长.
2.(2023·河南·校联考二模)记的内角A,B,C所对的边分别为a,b,c,已知.
(1)求A;
(2)设的中点为D,若,且的周长为,求a,b.
3.(2023·黑龙江大庆·大庆中学校考模拟预测)在①;②,这两个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角、、所对的边分别为、、,____________.
(1)求的值;
(2)若的面积为,,求的周长.
考法四 爪型三角形
【例4-1】(2023·全国·统考高考真题)已知在中,.
(1)求;
(2)设,求边上的高.
【例4-2】(2023·湖北)△ABC的内角A,B,C的对边分别为a,b,c.已知.
(1)求B.
(2)若,,___________,求.
在①D为AC的中点,②BD为∠ABC的角平分线这两个条件中任选一个,补充在横线上.
注:如果选择多个条件分别解答,按第一个解答计分.
【例4-3】(2023·福建泉州·统考模拟预测)的内角所对的边分别为,且满足.
(1)求;
(2)若平分,且,,求的面积.
【变式】
1.(2023·福建宁德·校考二模)已知的内角,,的对边分别为,,,且.
(1)求;
(2)若,,为中点,求的长.
2.(2022秋·江苏南京·高三校考期末)已知a,b,c分别是三个内角A,B,C的对边,面积为S,且.
(1)求A;
(2)若a=2,且角A的角平分线交BC于点D,AD=,求b.
3.(2023·河南·模拟预测)在中,内角A,B,C的对边分别是a,b,c,的面积记为S,已知,.
(1)求A;
(2)若BC边上的中线长为1,AD为角A的角平分线,求CD的长.
考法五 多边多角
【例5-1】(2023秋·陕西商洛·高三陕西省山阳中学校联考阶段练习)如图,在平面四边形ABCD中,,,,.
(1)求;
(2)若,求BC.
【例5-2】(2023秋·四川绵阳·高三四川省绵阳江油中学校考阶段练习)如图,在平面四边形中,,,,,.
(1)求的值;
(2)求的长.
【变式】
1.(2023春·广东湛江)如图,四边形ABCD的内角,,,,且.
(1)求角B;
(2)若点是线段上的一点,,求的值.
2.(2023春·浙江金华 )如图,四边形是由与正拼接而成,设,.
(1)当时,设,求,的值;
(2)当时,求线段的长.
3(2023广东)在三角形ABC中,,,,,.
(1)求BD的长;
(2)若AC与BD交于点O,求的面积.
考法六 最值
【例6-1】(2023·云南·校联考模拟预测)的内角的对边分别为,且.
(1)求角;
(2)若,求周长的取值范围.
【例6-2】.(2023秋·江苏·高三统考期末)已知△ABC为锐角三角形,内角A,B,C的对边分别为a,b,c,且acsB+bcsA=2ccsC.
(1)求角C;
(2)若c=2,求△ABC的周长的取值范围.
【例6-3】(2022·全国·统考高考真题)记的内角A,B,C的对边分别为a,b,c,已知.
(1)若,求B;
(2)求的最小值.
【变式】
1.(2023·江西·校联考模拟预测)已知中内角,,所对边分别为,,,.
(1)求;
(2)若边上一点,满足且,求的面积最大值.
2.(2023·江西九江·统考一模)中,内角所对的边分别是,已知,.
(1)求角的值;
(2)求边上高的最大值.
3.(2023·江苏南京·南京航空航天大学附属高级中学校考模拟预测)在中,以,,分别为内角,,的对边,且
(1)求;
(2)若,,求边上中线长.
4.(2022秋·江苏南京·高三校考期末)已知a,b,c分别是三个内角A,B,C的对边,面积为S,且.
(1)求A;
(2)若a=2,且角A的角平分线交BC于点D,AD=,求b.
考法七 三角形的四心
【例7】(2023春·浙江温州 )已知的内角、、的对边分别为、、,且,角B为钝角.
(1)求;
(2)在①重心,②内心,③外心这三个条件中选择一个补充在下面问题中,并解决问题.
若,,为的___________,求的面积.
【变式】
1.(2022·安徽·芜湖一中校联考一模)已知ΔABC的内角A,B,C的对边分别为a,b,c,tanC=
(1)求的值;
(2)设M和N分别是ΔABC的重心和内心,若MN//BC且c=2,求a的值.
2.(2022秋·四川内江·高三威远中学校校考期中)的内角A,B,C所对的边分别为.
(1)求A的大小;
(2)M为内一点,的延长线交于点D,___________,求的面积.
请在下面三个条件中选择一个作为已知条件补充在横线上,使存在,并解决问题.
①M为的重心,;
②M为的内心,;
③M为的外心,.
3.(2022秋·广东广州·高三广州市第五中学校考阶段练习)已知的内角、、的对边分别为、、,且.
(1)求;
(2)在①重心,②内心,③外心这三个条件中选择一个补充在下面问题中,并解决问题.
若,,为的___________,求的面积.
注:如果选择多个条件分别解答,则按第一个解答计分.
考法八 解三角形与三角函数性质的综合
【例8】(2023·广东)设函数,其中向量,.
(1)求的最小值;
(2)在△中,,,分别是角,,所对的边,已知,,△的面积为,求的值.
【例8-2】(2023·北京)已知函数,将的图象横坐标变为原来的,纵坐标不变,再向左平移个单位后得到的图象,且在区间内的最大值为.
(1)求的值;
(2)在锐角中,若,求的取值范围.
【变式】
1.(2023春·山西晋城)已知函数.
(1)求函数的定义域和值域;
(2)已知锐角的三个内角分别为A,B,C,若,求的最大值.
2.(2023·上海浦东新·华师大二附中校考模拟预测)已知函数.
(1)求函数的单调递减区间;
(2)在中,内角A,B,C的对边分别为a,b,c,且满足,求的取值范围.
3.(2023春·云南)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)在锐角中,角,,所对的边分别为,,,若,,且的面积为,求.
考法九 证明题
【例9】(2022·全国·统考高考真题)记的内角A,B,C的对边分别为a,b,c﹐已知.
(1)若,求C;
(2)证明:
【变式】
1.(2023·四川成都·校联考模拟预测)记的内角A,B,C的对边分别为a,b,c,且.
(1)求证:,,是等差数列;
(2)求的最大值.
2.(2023·山东泰安·校考模拟预测)在锐角中,内角所对的边分别为,满足,且.
(1)求证:;
(2)已知是的平分线,若,求线段长度的取值范围.
3.(2023·河南·校联考模拟预测)已知的外心为,点分别在线段上,且恰为的中点.
(1)若,求面积的最大值;
(2)证明:.
考法十 存在性与唯一性
【例10-1】(2021·全国·统考高考真题)在中,角、、所对的边长分别为、、,,..
(1)若,求的面积;
(2)是否存在正整数,使得为钝角三角形?若存在,求出的值;若不存在,说明理由.
【例10-2】.(2021·北京·统考高考真题)在中,,.
(1)求;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使存在且唯一确定,求边上中线的长.
条件①:;
条件②:的周长为;
条件③:的面积为;
【变式】
1.(2023·四川南充·四川省南充高级中学校考三模)在中,角的对边分别为,且.
(1)求的值;
(2)若,从下列三个条件中选出一个条件作为已知,使得存在且唯一确定,求的面积.
条件①:;条件②:;条件③:的周长为9.
2.(2022·北京·景山学校模拟预测)△ABC的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;
(2)从以下条件中选择两个,使△ABC存在且唯一确定,并求△ABC的面积.
①若;②;③;④△ABC的周长为9.
3.(2022秋·山西运城·高三校考阶段练习)中,内角的对边分别为的外接圆半径为,已知.
(1)求;
(2)已知的平分线交于点,从以下三个条件中选择两个,使唯一确定,并求和的长度.
条件①:;条件②:;条件③:.
专题01 解三角形(解答题)
考法一 公式的直接运用
【例1】(2023·天津·统考高考真题)在中,角所对的边分别是.已知.
(1)求的值;
(2)求的值;
(3)求.
【答案】(1)
(2)
(3)
【解析】(1)由正弦定理可得,,即,解得:;
(2)由余弦定理可得,,即,
解得:或(舍去).
(3)由正弦定理可得,,即,解得:,而,
所以都为锐角,因此,,
.
【变式】
1.(2022·天津·统考高考真题)在中,角A、B、C的对边分别为a,b,c.已知.
(1)求的值;
(2)求的值;
(3)求的值.
【答案】(1)
(2)
(3)
【解析】(1)因为,即,而,代入得,解得:.
(2)由(1)可求出,而,所以,又,所以.
(3)因为,所以,故,又, 所以,,而,所以,
故.
2.(2022·浙江·统考高考真题)在中,角A,B,C所对的边分别为a,b,c.已知.
(1)求的值;
(2)若,求的面积.
【答案】(1);
(2).
【解析】(1)由于, ,则.因为,
由正弦定理知,则.
(2)因为,由余弦定理,得,
即,解得,而,,
所以的面积.
3.(2023·天津北辰·校考模拟预测)已知,,分别为锐角三角形三个内角的对边,且.
(1)求;
(2)若,,求;
(3)若,求的值.
【答案】(1)
(2)3
(3)
【解析】(1)由于,所以,
由根据正弦定理可得,
所以,且三角形为锐角三角形,即
所以.
(2)在中,由余弦定理知,
即,解得或(舍),
故.
(3)由,可得,
所以,
,
即
考法二 三角形的面积
【例2-1】(2023·福建·校联考模拟预测)设的内角,,的对边分别为,,,已知,,且.
(1)求;
(2)求的面积.
【答案】(1)(2)
【解析】(1)由及,得,
由正弦定理得
所以,,所以,又因为,所以.
(2)由结合正弦定理得,即所以或.
又因为,所以.所以,
因为,所以,
所以,即的面积为.
【例2-2】(2023·湖南永州·统考一模)在中,设所对的边分别为,且满足.
(1)求角;
(2)若的内切圆半径,求的面积.
【答案】(1)(2)
【解析】(1)在中,由得,
即,
故,由于,
故,而,故.
(2)由可得,而,
故,则,
由的内切圆半径,可得,
即,即,
故,解得,
故的面积.
【变式】
1.(2023·海南海口·校考模拟预测)在 中,角 A、B 、C 的对边分别为a 、b 、c ,且满足.
(1)求的值;
(2)若,求的面积.
【答案】(1)2(2)12
【解析】(1)由可得,
,
因为,所以可得,
解得.
(2)由(1)知,所以,
又因为,所以,
所以,
即,又,
所以,
由正弦定理可得,,
所以,
所以,
所以的面积.
2.(2023·江苏无锡·校考模拟预测)已知函数.
(1)求函数的最小正周期和单调递增区间;
(2)在中,内角所对的边分别是,且,若,求的面积.
【答案】(1)最小正周期为,单调递增区间为.(2)
【解析】(1),
所以函数的最小正周期为.
令,得,
故函数的单调递增区间为.
(2)由,得,
由得,所以,得.
由余弦定理得,即,
因为,所以,
从而有,得,
则
3.(2023·河南开封·统考三模)在中,设A,B,C所对的边分别为a,b,c,且满足.
(1)求角B;
(2)若,的内切圆半径,求的面积.
【答案】(1)(2)
【解析】(1)因为,
由余弦定理得,即,所以.
又,所以
(2)由余弦定理得:,则,
由三角形面积公式,,即,
则,
所以,解得,
所以.
考法 三角形的周长
【例3-1】(2023·山东菏泽)在中,角所对的边分别为已知,面积,再从以下两个条件中选择其中一个作为已知,求三角形的周长.
(1);
(2).
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】
【解析】由三角形的面积公式可知,,,整理得
由正弦定理得:
因为,,
若选择条件(1)由:得,则,
又为三角形的内角,,由正弦定理得
代入解得,三角形的周长为
若选择条件(2),则由,得
又,
又为三角形的内角,.
由正弦定理得: ,代入解得,三角形的周长为
【例3-2】(2023·重庆南岸)设,
(1)求的单调递增区间;
(2)在中,角为锐角,角,,的对边分别为,,,若,,,求三角形的周长.
【答案】(1);(2)
【解析】(1)由已知,
令,
则,
的单调递增区间为;
(2)由(1)得,又角为锐角,
,得,
,
得,所以三角形的周长为.
【变式】
1.(2022·北京·统考高考真题)在中,.
(1)求;
(2)若,且的面积为,求的周长.
【答案】(1)(2)
【解析】(1)解:因为,则,由已知可得,
可得,因此,.
(2)解:由三角形的面积公式可得,解得.
由余弦定理可得,,
所以,的周长为.
2.(2023·河南·校联考二模)记的内角A,B,C所对的边分别为a,b,c,已知.
(1)求A;
(2)设的中点为D,若,且的周长为,求a,b.
【答案】(1)
(2),.
【解析】(1)由条件及正弦定理可得,
因为,所以,
所以,整理得,
又因为,所以,
所以,解得.
(2)在中,由余弦定理得.
而,,所以.①
在中,由余弦定理得.②
由①②两式相减,得,所以,
将代入②,得,则.
因为的周长为,
所以,解得,
所以,.
3.(2023·黑龙江大庆·大庆中学校考模拟预测)在①;②,这两个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角、、所对的边分别为、、,____________.
(1)求的值;
(2)若的面积为,,求的周长.
【答案】(1)(2)
【解析】(1)解:若选①,由已知得,所以,
由正弦定理得,
又,所以,所以,
又,由,,解得;
若选②,由已知及正弦定理得,
所以,
所以,
所以,
又,所以,所以,
又,由,,解得.
(2)解:由的面积为,得,所以,
由(1)可得,
由余弦定理得,
所以,所以,
所以的周长为.
考法四 爪型三角形
【例4-1】(2023·全国·统考高考真题)已知在中,.
(1)求;
(2)设,求边上的高.
【答案】(1)(2)6
【解析】(1),,即,
又,
,
,,即,所以,.
(2)由(1)知,,
由,
由正弦定理,,可得,
,.
【例4-2】(2023·湖北)△ABC的内角A,B,C的对边分别为a,b,c.已知.
(1)求B.
(2)若,,___________,求.
在①D为AC的中点,②BD为∠ABC的角平分线这两个条件中任选一个,补充在横线上.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)(2)答案见解析
【解析】(1)由正弦定理得,.
因为,所以,所以,即.
又,则,所以.
(2)选择条件①:因为,所以,,
.
选择条件②:
因为BD为∠ABC的角平分线,所以,
则,
解得.
【例4-3】(2023·福建泉州·统考模拟预测)的内角所对的边分别为,且满足.
(1)求;
(2)若平分,且,,求的面积.
【答案】(1)(2)
【解析】(1)解法一:因为,
所以由正弦定理可得,
即,,
所以,
又,所以,
因为,所以.
解法二:在中,由余弦定理得,,
又因为,所以,
即,
所以,
因为,所以.
(2)解法一:因为,
所以,
两边平方得,即①,
又因为平分,所以,即②,
由①②,解得,,
所以.
解法二:在中,,所以,
又因为平分,所以,即①,
在中,由余弦定理,得,即②,
在中,由余弦定理,得,即③,
由①②③解得,,
所以.
解法三:过点作交于点,
因为,且平分,所以,
所以为等边三角形,所以,
又因为,所以,,
所以.
【变式】
1.(2023·福建宁德·校考二模)已知的内角,,的对边分别为,,,且.
(1)求;
(2)若,,为中点,求的长.
【答案】(1)(2)
【解析】(1),即,
化简得,解得,
因为,所以.
(2)由余弦定理得,
即,解得,
因为
,故的长度为.
2.(2022秋·江苏南京·高三校考期末)已知a,b,c分别是三个内角A,B,C的对边,面积为S,且.
(1)求A;
(2)若a=2,且角A的角平分线交BC于点D,AD=,求b.
【答案】(1)(2)2
【解析】(1)解:由题知,
则有:①,
在中,由余弦定理可得:
,
代入①式可得: ,
即,
由辅助角公式可得:,
所以或,
即或,
因为,所以;
(2)由(1)知,因为平分,
所以,
且有,
即:,
将边和角代入可得: ,
化简可得: ,
在中,由余弦定理可得:
,
即,
即,
解得:(舍)或,
即,解得.
3.(2023·河南·模拟预测)在中,内角A,B,C的对边分别是a,b,c,的面积记为S,已知,.
(1)求A;
(2)若BC边上的中线长为1,AD为角A的角平分线,求CD的长.
【答案】(1)(2)
【解析】(1)因为,所以,即,
由正弦定理可得,即
所以.
因为,所以.
(2)设AE为BC边上的中线,可得,
如下图所示:
则,
所以,解得.
因为,
所以,
所以;由可得,
利用余弦定理可得,
所以.
考法五 多边多角
【例5-1】(2023秋·陕西商洛·高三陕西省山阳中学校联考阶段练习)如图,在平面四边形ABCD中,,,,.
(1)求;
(2)若,求BC.
【答案】(1)
(2)
【解析】(1)在中,由正弦定理得,即,
所以.由题设知,所以.
(2)由题设及(1)知,,
在中,由余弦定理得
,
所以.
【例5-2】(2023秋·四川绵阳·高三四川省绵阳江油中学校考阶段练习)如图,在平面四边形中,,,,,.
(1)求的值;
(2)求的长.
【答案】(1)
(2)
【解析】(1)解:在中,,,,
由余弦定理可得,
整理可得,,解得,则,
故为等腰三角形,故.
(2)解:由(1)知,,又因为,则,
因为,则为锐角,
且,
所以,
,
在中,由正弦定理,
可得.
【变式】
1.(2023春·广东湛江)如图,四边形ABCD的内角,,,,且.
(1)求角B;
(2)若点是线段上的一点,,求的值.
【答案】(1)
(2)
【解析】(1)设,
在中由余弦定理得,即①,
又在中由余弦定理得,即②,
因为,则,
联立①②可得(负值舍去),,因为,所以.
(2)在中,由正弦定理知,,
所以,
又,故,
在直角三角形中,由勾股定理知,,
此时.
2.(2023春·浙江金华 )如图,四边形是由与正拼接而成,设,.
(1)当时,设,求,的值;
(2)当时,求线段的长.
【答案】(1),
(2)
【解析】(1)在中,由,
可知.
由于,,,
,,,.
(2)在中,,
所以,,
.
3(2023广东)在三角形ABC中,,,,,.
(1)求BD的长;
(2)若AC与BD交于点O,求的面积.
【答案】(1)
(2)
【解析】(1)由题意,在中,,,,
由余弦定理得,,
所以,
在中,,
所以,
所以,
在中,由余弦定理可知,
所以.
(2)由(1)可知,又因为,所以为等边三角形,
所以,,
在中,,所以,
在中,,
故,
所以,
所以,
在中,由正弦定理可知,即,解得,
所以.
考法六 最值
【例6-1】(2023·云南·校联考模拟预测)的内角的对边分别为,且.
(1)求角;
(2)若,求周长的取值范围.
【答案】(1)(2)
【解析】(1)因为,可得,
所以由正弦定理可得,
又为三角形内角,,
所以,
因为,
所以,可得,所以.
(2)由(1)知,又,
由正弦定理得,
则,
,
【例6-2】.(2023秋·江苏·高三统考期末)已知△ABC为锐角三角形,内角A,B,C的对边分别为a,b,c,且acsB+bcsA=2ccsC.
(1)求角C;
(2)若c=2,求△ABC的周长的取值范围.
【答案】(1)(2)
【解析】(1)由正弦定理,得,
即,即,
又,所以,
所以,故.
(2)由正弦定理,得,
所以的周长
由为锐角三角形可知,,得,
所以,所以.
所以的周长的取值范围为.
【例6-3】(2022·全国·统考高考真题)记的内角A,B,C的对边分别为a,b,c,已知.
(1)若,求B;
(2)求的最小值.
【答案】(1);
(2).
【解析】(1)因为,即,
而,所以;
(2)由(1)知,,所以,
而,
所以,即有,所以
所以
.
当且仅当时取等号,所以的最小值为.
【变式】
1.(2023·江西·校联考模拟预测)已知中内角,,所对边分别为,,,.
(1)求;
(2)若边上一点,满足且,求的面积最大值.
【答案】(1)
(2).
【解析】(1)由题意,,
由正弦定理得,
因为三角形内角,,
则,即,
,,,
故,,
(2),
已知,,由(1)知,,
由题意得由,(如图)
已知,且由(1)知,
两边平方得,
则
,
解得,.故.
当且仅当,即时,等号成立.
所以,的最大值为.
2.(2023·江西九江·统考一模)中,内角所对的边分别是,已知,.
(1)求角的值;
(2)求边上高的最大值.
【答案】(1)
(2)
【解析】(1)由,得
由正弦定理,得
又,
即
,
(2)解法一:设边上高为,
由余弦定理,得
即
,,即,当且仅当时,等号成立
又,,边上高的最大值为
解法二:设边上高为,
由正弦定理得,,
因为,,
,,,
又,,边上高的最大值为.
3.(2023·江苏南京·南京航空航天大学附属高级中学校考模拟预测)在中,以,,分别为内角,,的对边,且
(1)求;
(2)若,,求边上中线长.
【答案】(1)
(2)或
【解析】(1)由得,
由正弦定理可得,
由余弦定理可得,
因为,所以.
(2)因,由正弦定理可得,
即,因为,所以,则,
所以或,即或,
当时,为等边三角形,即,如图所示,
所以边上中线长为;
当时,则,所以为直角三角形,如图所示,
又,所以由正弦定理,即,
所以,,所以边上中线长为;
综上可得边上中线长为或.
4.(2022秋·江苏南京·高三校考期末)已知a,b,c分别是三个内角A,B,C的对边,面积为S,且.
(1)求A;
(2)若a=2,且角A的角平分线交BC于点D,AD=,求b.
【答案】(1)(2)2
【解析】(1)解:由题知,
则有:①,
在中,由余弦定理可得:
,
代入①式可得: ,
即,
由辅助角公式可得:,
所以或,
即或,
因为,所以;
(2)由(1)知,因为平分,
所以,
且有,
即:,
将边和角代入可得: ,
化简可得: ,
在中,由余弦定理可得:
,
即,
即,
解得:(舍)或,
即,解得.
考法七 三角形的四心
【例7】(2023春·浙江温州 )已知的内角、、的对边分别为、、,且,角B为钝角.
(1)求;
(2)在①重心,②内心,③外心这三个条件中选择一个补充在下面问题中,并解决问题.
若,,为的___________,求的面积.
【答案】(1);
(2)若选①,;若选②,;若选③,
【解析】(1)由正弦定理可得,因为,所以.
因为,所以.
(2)若选①,连接并延长交边于点,
因为为的重心,所以为的中点,且,
所以点到的距离等于点到的距离的,
所以,;
若选②,由余弦定理可得,
若为的内心,设的内切圆的半径为,
则,则,
因此,;
若选③,若为的外心,设的外接圆半径为,
由余弦定理可得,则,
在优弧上任取一点,则,则,
因此,.
【变式】
1.(2022·安徽·芜湖一中校联考一模)已知ΔABC的内角A,B,C的对边分别为a,b,c,tanC=
(1)求的值;
(2)设M和N分别是ΔABC的重心和内心,若MN//BC且c=2,求a的值.
【答案】(1)2
(2)
【解析】(1)由已知得,,即sinAcsC=2sinC-csAsinC得sin(A+C)=2sinC即sinB=2sinC
由正弦定理得,所以;
(2)由(1)知,因为,所以
设△ABC的内切圆半径为r,则内心N到BC边的距离为r,
因为MN∥BC,所以重心M到BC边的距离为r,根据重心的性质,顶点A到BC边的距离为3r,
根据面积关系得
即,
所以
2.(2022秋·四川内江·高三威远中学校校考期中)的内角A,B,C所对的边分别为.
(1)求A的大小;
(2)M为内一点,的延长线交于点D,___________,求的面积.
请在下面三个条件中选择一个作为已知条件补充在横线上,使存在,并解决问题.
①M为的重心,;
②M为的内心,;
③M为的外心,.
【答案】(1)
(2)答案见解析
【解析】(1)∵,∴,即
由正弦定理得,,即,
∵,∴,∴,又,∴,∴
(2)设外接圆半径为,则根据正弦定理得,,
若选①:∵M为该三角形的重心,则D为线段的中点且,
又,∴,
即, 又由余弦定理得,即,解得,∴;
若选②:∵M为的内心,∴,由得,∵,∴,即,
由余弦定理可得,即,∴,
即,∵,∴, ∴.
若选③:M为的外心,则为外接圆半径,,与所给条件矛盾,故不能选③.
3.(2022秋·广东广州·高三广州市第五中学校考阶段练习)已知的内角、、的对边分别为、、,且.
(1)求;
(2)在①重心,②内心,③外心这三个条件中选择一个补充在下面问题中,并解决问题.
若,,为的___________,求的面积.
注:如果选择多个条件分别解答,则按第一个解答计分.
【答案】(1)
(2)答案见解析
【解析】(1)解:,
,
则,即,
,则,,即有,
可得,
,则,,解得.
(2)解:若选①,连接并延长交边于点,
因为为的重心,所以,为的中点,且,
所以点到的距离等于点到的距离的,
所以,;
若选②,由余弦定理可得,
若为的内心,设的内切圆的半径为,
则,则,
因此,;
若选③,若为的外心,设的外接圆半径为,
由余弦定理可得,则,
在优弧上任取一点,则,则,
因此,.
考法八 解三角形与三角函数性质的综合
【例8】(2023·广东)设函数,其中向量,.
(1)求的最小值;
(2)在△中,,,分别是角,,所对的边,已知,,△的面积为,求的值.
【答案】(1);
(2).
【解析】(1)由题设,,
所以,当时的最小值为.
(2)由,得:,则,又,
所以,故,则.
由,可得:.
在△中,由余弦定理得:,
所以.
由,则.
【例8-2】(2023·北京)已知函数,将的图象横坐标变为原来的,纵坐标不变,再向左平移个单位后得到的图象,且在区间内的最大值为.
(1)求的值;
(2)在锐角中,若,求的取值范围.
【答案】(1);(2).
【解析】(1)将函数的图象横坐标变为原来的,纵坐标不变,再向左平移个单位后得到的图象,
则,
,,
当,即时,最大值,所以,;
(2),
,则,所以,,所以,,
,
是锐角三角形,由,解得,
所以,,,则.
【变式】
1.(2023春·山西晋城)已知函数.
(1)求函数的定义域和值域;
(2)已知锐角的三个内角分别为A,B,C,若,求的最大值.
【答案】(1);
(2)2
【解析】(1),
所以要使有意义,
只需,即,
所以,解得
所以函数的定义域为,
由于,所以,
所以函数的值域为;
(2)由于,所以,
因为,所以,所以即,
由锐角可得,所以,
由正弦定理可得,
因为,所以所以,
所以的最大值为2.
2.(2023·上海浦东新·华师大二附中校考模拟预测)已知函数.
(1)求函数的单调递减区间;
(2)在中,内角A,B,C的对边分别为a,b,c,且满足,求的取值范围.
【答案】(1)
(2)
【解析】(1)
令,则
所以,单调减区间是.
(2)由得:
,即,
由于,所以.
在中,,
,
于是,则,,
,所以.
3.(2023春·云南)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)在锐角中,角,,所对的边分别为,,,若,,且的面积为,求.
【答案】(1);(2).
【解析】(1)据图象可得,故,
由得:.
由得:.
由知,,
,解得,
;
(2),,
,,
,,
由题意得的面积为,解得,
由余弦定理得,解得:.
考法九 证明题
【例9】(2022·全国·统考高考真题)记的内角A,B,C的对边分别为a,b,c﹐已知.
(1)若,求C;
(2)证明:
【答案】(1);
(2)证明见解析.
【解析】(1)由,可得,,而,所以,即有,而,显然,所以,,而,,所以.
(2)由可得,
,再由正弦定理可得,
,然后根据余弦定理可知,
,化简得:
,故原等式成立.
【变式】
1.(2023·四川成都·校联考模拟预测)记的内角A,B,C的对边分别为a,b,c,且.
(1)求证:,,是等差数列;
(2)求的最大值.
【答案】(1)证明见解析
(2).
【解析】(1)证明:因为,
所以,
由正弦定理,得,
又由余弦定理,得
,
则,即,
所以,,是等差数列.
(2)解:由(1)得,
又(当且仅当时取等号),
因为,所以,则的最大值为,
则的最大值为.
2.(2023·山东泰安·校考模拟预测)在锐角中,内角所对的边分别为,满足,且.
(1)求证:;
(2)已知是的平分线,若,求线段长度的取值范围.
【答案】(1)证明见解析
(2)
【解析】(1)由题意得,即.
所以,
由正弦定理得,又由余弦定理得,
所以,故,
故,整理得.
又为锐角三角形,则,,,
所以,因此.
(2)在中,由正弦定理得,所以.
所以.因为为锐角三角形,且,
所以,解得.
故,所以.因此线段长度的取值范围.
3.(2023·河南·校联考模拟预测)已知的外心为,点分别在线段上,且恰为的中点.
(1)若,求面积的最大值;
(2)证明:.
【答案】(1)
(2)证明见解析
【解析】(1)解:由正弦定理,得,
所以,
又,所以或,
当时,
由余弦定理,得
,
所以,的面积,
当且仅当时,取等号;
当时,
同理可得,的面积,
当且仅当时,取等号.
综上,面积的最大值为;
(2)证明:设,
由余弦定理知,,
因为,
所以,
化简整理得,
而,因此,
又因为是外心,故,
同理可知,
因为恰为的中点,
因此,所以.
考法十 存在性与唯一性
【例10-1】(2021·全国·统考高考真题)在中,角、、所对的边长分别为、、,,..
(1)若,求的面积;
(2)是否存在正整数,使得为钝角三角形?若存在,求出的值;若不存在,说明理由.
【答案】(1);(2)存在,且.
【解析】(1)因为,则,则,故,,
,所以,为锐角,则,
因此,;
(2)显然,若为钝角三角形,则为钝角,
由余弦定理可得,
解得,则,
由三角形三边关系可得,可得,,故.
【例10-2】.(2021·北京·统考高考真题)在中,,.
(1)求;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使存在且唯一确定,求边上中线的长.
条件①:;
条件②:的周长为;
条件③:的面积为;
【答案】(1);(2)答案不唯一,具体见解析.
【解析】(1),则由正弦定理可得,
,,,,
,解得;
(2)若选择①:由正弦定理结合(1)可得,
与矛盾,故这样的不存在;
若选择②:由(1)可得,
设的外接圆半径为,
则由正弦定理可得,
,
则周长,
解得,则,
由余弦定理可得边上的中线的长度为:
;
若选择③:由(1)可得,即,
则,解得,
则由余弦定理可得边上的中线的长度为:
.
【变式】
1.(2023·四川南充·四川省南充高级中学校考三模)在中,角的对边分别为,且.
(1)求的值;
(2)若,从下列三个条件中选出一个条件作为已知,使得存在且唯一确定,求的面积.
条件①:;条件②:;条件③:的周长为9.
【答案】(1)2
(2)答案见解析
【解析】(1)解:因为,
由正弦定理得,
即,
又因为,可得,
所以,可得.
(2)解:由(1)得,由正弦定理得,
若选条件①:由余弦定理得,即,
又由,解得,则,此时存在且唯一确定,
因为,则,可得,
所以;
若选条件②:由,因为,即,
若为锐角,则,
由余弦定理,即,
整理得,且,解得,则;
若为钝角,则,
由余弦定理得,即,
整理得,且,解得,则;
综上所述,此时存在但不唯一确定,不合题意;
若条件③:因为,即,解得,则,
所以此时存在且唯一确定,
由余弦定理得,
因为,可得,
所以.
2.(2022·北京·景山学校模拟预测)△ABC的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;
(2)从以下条件中选择两个,使△ABC存在且唯一确定,并求△ABC的面积.
①若;②;③;④△ABC的周长为9.
【答案】(1);(2)选①④,面积为.
【解析】(1)因为,由正弦定理得,
,
三角形中,所以,,所以;
(2)因为,所以,因此条件③不能确定三角形;
若已知①②,则由正弦定理得,无解;
若已知①④,即,,则,与三角形的性质矛盾,三角形不存在.
所以只有条件②④能确定三角形.,,则,由(1),
,即,所以,
,,又,所以,从而,
为等边三角形,唯一确定,面积为.
3.(2022秋·山西运城·高三校考阶段练习)中,内角的对边分别为的外接圆半径为,已知.
(1)求;
(2)已知的平分线交于点,从以下三个条件中选择两个,使唯一确定,并求和的长度.
条件①:;条件②:;条件③:.
【答案】(1)
(2)选择条件②和③;,
【解析】(1)由已知得,
得,
即,即,
又因为,故;
(2)由(1)得中,
由余弦定理得,
所以,
而条件①中,所以,显然不符合题意,即条件①错误,
由条件②,条件③,解得,
由余弦定理可得,
所以,所以,
在中,因为为的平分线,
所以,
又因为,所以,
在中,,
所以.
相关试卷
这是一份2024年高考数学二轮复习专题06导数(解答题10种考法)专练(原卷版+解析),共78页。试卷主要包含了已知函数.,设函数,设函数,.,已知函数和有相同的最小值,已知函数,已知函数,,已知函数,.等内容,欢迎下载使用。
这是一份2024年高考数学二轮复习专题05解析几何(解答题10种考法)讲义(原卷版+解析),共79页。试卷主要包含了定点,定值,定直线,最值,轨迹问题,长度比值,存在性,角度关系转斜率等内容,欢迎下载使用。
这是一份2024年高考数学二轮复习专题02数列(解答题12种考法)(精练)(原卷版+解析),共47页。试卷主要包含了已知数列中,,,已知等比数列的前项和为,且,已知数列的前n项和为,,且,已知数列满足,记为数列的前n项和,已知.等内容,欢迎下载使用。









