2024年陕西省宝鸡市陈仓区中考一模数学试题

这是一份2024年陕西省宝鸡市陈仓区中考一模数学试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
命题人：颜嘉睿 审核人：郭宁春
一、选择题（共8小题，每小题，3分满分24分）
1．的值是（ ）
A．B．1C．D．
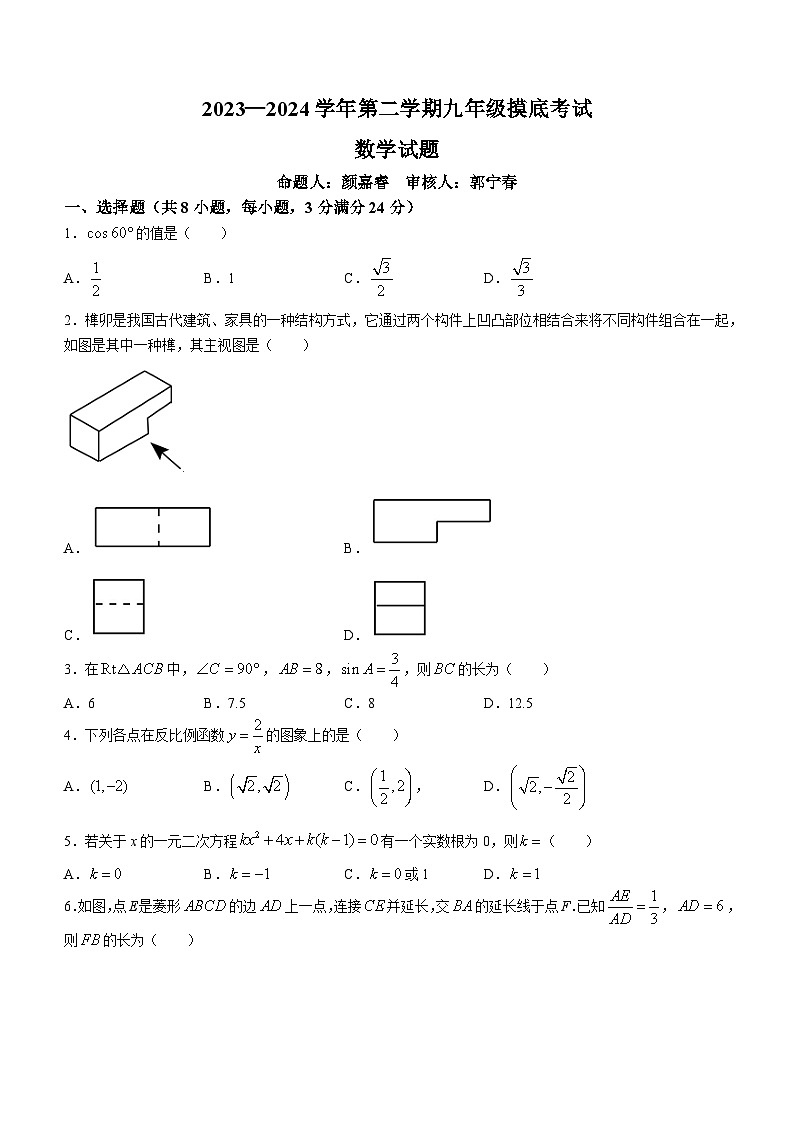
2．榫卯是我国古代建筑、家具的一种结构方式，它通过两个构件上凹凸部位相结合来将不同构件组合在一起，如图是其中一种榫，其主视图是（ ）
A．B．
C．D．
3．在中，，，，则的长为（ ）
A．6B．7.5C．8D．12.5
4．下列各点在反比例函数的图象上的是（ ）
A．B．C．，D．
5．若关于x的一元二次方程有一个实数根为0，则（ ）
A．B．C．或1D．
6．如图，点E是菱形的边上一点，连接并延长，交的延长线于点F．已知，，则的长为（ ）
A．6B．12C．9D．4.5
7．如图，是的直径，垂直于弦于点D，的延长线交于点E．若，，则的长是（ ）
A．1B．C．2D．4
8．把抛物线先向右平移4个单位长度，再向下平移5个单位长度得到抛物线．若点，都在抛物线上，且，则（ ）
A．B．C．D．
二、填空题（共6小题，每小题3分，满分18分）
9．若，则__________．
10．在一个圆的内接正多边形中，一条边所对的圆心角为，则该正多边形的一个外角的度数是__________．
11．已知菱形的面积为，对角线长为，则对角线__________厘米．
12．如图，为的直径，射线交于点F，点C为劣弧的中点，连接．若，，则弧的长为__________．
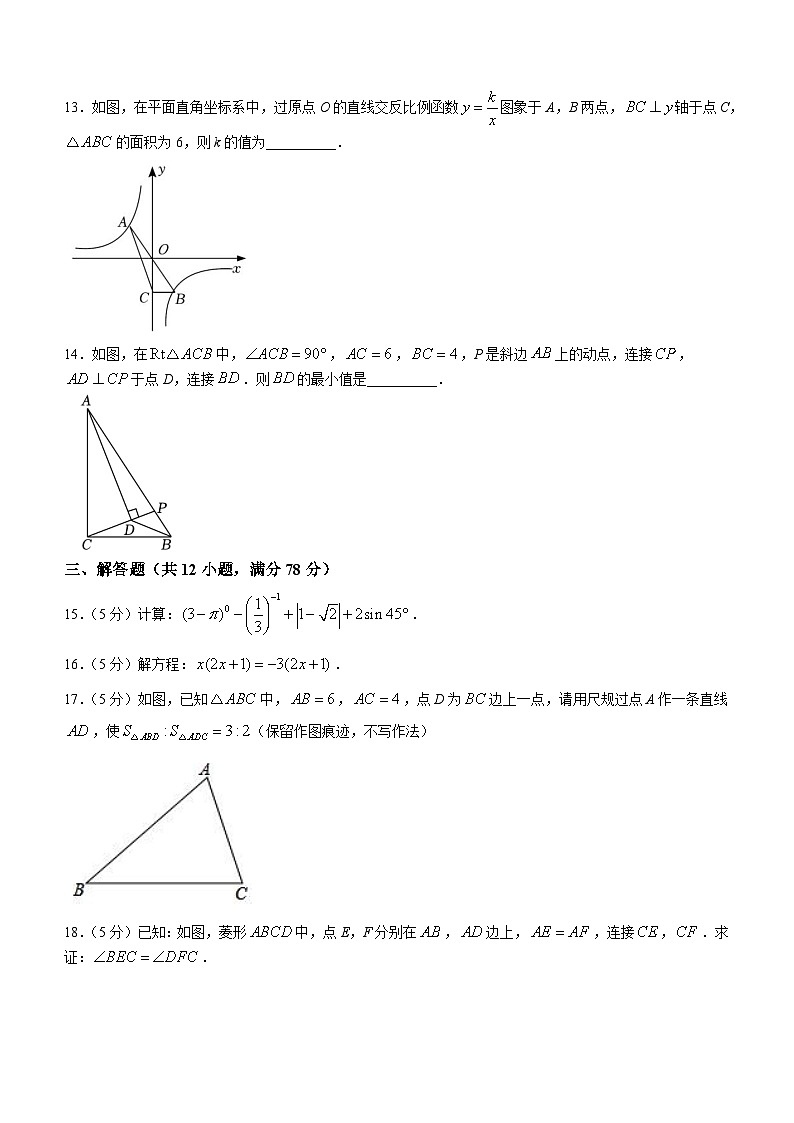
13．如图，在平面直角坐标系中，过原点O的直线交反比例函数图象于A，B两点，轴于点C，的面积为6，则k的值为__________．
14．如图，在中，，，，P是斜边上的动点，连接，于点D，连接．则的最小值是__________．
三、解答题（共12小题，满分78分）
15．（5分）计算：．
16．（5分）解方程：．
17．（5分）如图，已知中，，，点D为边上一点，请用尺规过点A作一条直线，使（保留作图痕迹，不写作法）
18．（5分）已知：如图，菱形中，点E，F分别在，边上，，连接，．求证：．
19．（6分）中，，，点D在上，，，求的长．
20．（6分）如图所示，一次函数图象与反比例函数图象相交于点和点．
（1）求反比例函数解析式；
（2）当时，求x的取值范围．
21．（7分）2023年第19届亚运会在杭州举办．小蔡作为亚运会的志愿者“小青荷”为大家提供咨询服务．现有如图所示“杭州亚运会吉祥物”的三盒盲盒供小蔡选择，分别记为A，B，C．
求（1）小蔡随机抽取一盒，她抽到A的概率为__________．
（2）请用列表或画树状图的方法，求小蔡从中随机抽取两盒吉祥物恰是A和C的概率．
22．（7分）红色教育基地照金纪念广场上屹立着刘志丹，谢子长，习仲勋三位革命前辈的塑像，某数学兴趣小组计划在假期前往照金革命根据地学习，并测量塑像高度．活动方案如下：
测量方案：如图，点B、E、F、D四点在同一条直线上，在点E处放置平面镜，此时小明视线刚好在平面镜内看到塑像顶端C的像，在点F处安装测倾器，测得塑像顶端C的仰角约为
数据收集：测得眼睛离地面高度米，米，米，米，，，．
解决问题：求塑像的高度．（结果精确到0.1米；参考数据：，，）
23．（7分）某特产专卖店销售一种核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后经市场调查发现，单价每降低1元，平均每天的销售量可增加10千克．
（1）若该特产专卖店希望这批核桃每天获利2240元，则销售单价应定为多少元？
（2）当定价多少元时，销售单价为多少元时该店销售核桃每天获得利润最大，最大利润是多少？
24．（7分）如图，与的边相切于点B，与边相切于点D，与边交于点E，是的直径．
（1）求证：；
（2）若的半径是，，求的长．
25．（8分）掷实心球是宝鸡市高中阶段学校招生体育考试的选考项目．如图1是一名男生投实心球，实心球行进路线是一条抛物线，行进高度与水平距离之间的函数关系如图2所示，掷出时起点处高度为，当水平距离为时，实心球行进至最高点处．
（1）求y关于x的函数表达式；
（2）根据宝鸡市高中阶段学校招生体育考试男生评分标准，投掷过程中，实心球从起点到落地点的水平距离大于等于时，得分为满分10分．请计算说明该男生在此项考试中是否得满分．
26．（10分）
【问题提出】
（1）如图①，已知是面积为的等边三角形，是的平分线，则的长为__________．
【问题探究】
（2）如图②，在中，，，，点D为的中点，点E，F分别在边，上，且．证明：．
【问题解决】
（3）如图③，李叔叔准备在一块空地上修建一个矩形花园，然后将其分割种植三种不同的花卉．按照他的分割方案，点P，Q分别在，上，连接、、，，E、F分别在、上，连接、，，，其中四边形种植玫瑰，和种植郁金香，剩下的区域种植康乃馨，根据实际需要，要求种植玫瑰的四边形的面积为，为了节约成本，矩形花园的面积是否存在最小值？若存在，请求出矩形的最小面积，若不存在，请说明理由．
摸底考试参考答案
一、选择题1---4题ABAB5----8题DCCD
二、填空题9．7310．72°11．812．Π
13．—614．2
三、解答题（共12小题，满分78分）
15．（5分）解：原式．
16．（5分）解方程：x（2x+1）＝﹣3（2x+1）．
解：x（2x+1）+3（2x+1）＝0，
（2x+1）（x+3）＝0，
（2x+1）=0或（x+3）＝0，
解得，x2＝﹣3．
17．解：作∠BAC的角平分线交BC于D，直线AD即为所求．
18．证明：连接AC，
∵四边形ABCD是菱形，
∴∠BAC＝∠DAC，
∵AC＝AC，AE＝AF，
∴△AEC≌△AFC（SAS）
∴∠AEC＝∠AFC．
∴∠BEC＝∠DFC
19．解：∵∠A＝30°，∠BDC＝60°，
∴∠DBA＝60°﹣30°＝30°，
∴∠A＝∠DBA，
，
在Rt△BDC中，
20．解：（1）∵一次函数y1＝﹣x+m与反比例函数相交于点A（n，3）和点B（3，﹣1），
，
解得k＝﹣3，n=-1
∴反比例函数的解析式为；A(-1,3)
（2）观察图象可得，当y1＞y2时，x的取值范围为x＜﹣1或0＜x＜3．
21．解：（1）、小蔡随机抽取一盒，她抽到A的概率为1/3
(2)画树状图如下：
共有6种等可能的结果，其中小蔡抽到的两盒吉祥物恰好是A和C的结果有2种，
∴小蔡抽到的两盒吉祥物恰好是A和C的概率为．
22．解：因为AB⟂BD,GF⟂BD,CD⟂BD.所以∠ABE=∠CDE
有光的反射原理可知：∠AEB=∠CED
所以△ABE~△CDEABBE=CDDE=1.62=45
设CD=4x则DE=5x
过点G作GM垂直CD于M
在直角三角形CGM中CM=4X-1.4GM=DF=5X-4
tan∠CGM=CMGM=4X-1.45X-4=1.25=54
解得x=1.6
所以CD=4x=6.4m
答：塑像高为6.4m
23．解：
（1）、设每千克核桃应降价x元，由题意可得（100+10x）（60﹣x﹣40）=0
解的x1=4x2=6
经检验这两个解都适合题意
所以销售单价应定为54或56时，该特产专卖店这批核桃每天获利2240元
（2）设每千克核桃应降价x元，每天的总利润为y元，，
则y＝（100+10x）（60﹣x﹣40）
＝﹣10x2+100x+2000
＝﹣10（x﹣5）2+2250，
当x＝5时，定价60﹣x＝55（元），y最大，且y最大＝2250（元），
所以当定价55元时，该店销售核桃获得利润最大，最大利润是2250元；
24．（1）证明：连接OD，如图，
∵，⊙O与△ABC的BC边相切于点B，与AC边相切于点D，
∴CD＝CB，∠ODC＝∠OBC，
在△COD和△COB中，
，
∴△COD≌△COB（SAS），
∴∠COD＝∠COB，
，
∵OD＝OE，
，
∴∠DEO＝∠COB，
∴DE∥OC；
（2）在Rt△AOD中，，
，
∵∠OAD＝∠CAB，∠ADO＝∠ABC，
∴△AOD∽△ACB，
，即，解得BC＝3，
∵△COD≌△COB，
∴CD＝CB＝3．
25．（1）解：设顶点式y＝a（x﹣4）2+3（a≠0），
，
解得a＝-112，
∴y＝-112（x﹣4）2+3；
（2）令y＝0，即-112（x﹣4）2+3=0
解得x1＝10，x2＝﹣2（不合题意，舍去），
∵10＞9.60，
∴该男生在此项考试中得满分．
26．解：
（1）解：∵△ABC是等边三角形，AD是∠BAC的平分线，
∴AD⊥BC，BD＝CD，∠BAD＝30°，
，
，
解得AB＝4，
故答案为：4；
（2）证明：连接CD，
∵△ABC是等腰直角三角形，D是AB的中点，
∴CD⊥AB，CD＝AD，CD平分∠C，
∵∠EDF＝90°，
∴∠ADE+∠BDF＝∠BDF+∠CDF＝90°，
∴∠ADE＝∠CDF，
∵∠A＝∠FCD＝45°，
∴△ADE≌△CDF（ASA），
∴DE＝DF；
（3）解：过Q点作QG⊥BP交于G点，过点Q作QH⊥PC交于H点，
∵∠BPC＝60°，
∴∠GQH＝120°，
∵∠EQF＝120°，
∴∠EQG＝∠FQH，
∵QE＝QF，
∴△EQG≌△FQH（AAS），
∴QG＝QF，
∵QG⊥BP，QH⊥PC，
∴PQ是∠BPC的平分线，
∴∠BPQ＝∠CPQ＝30°，
∴∠PQG＝∠PQH＝60°，
∵S四边形QGPH＝S四边形QEPF＝64，
，即，
解得，
∴GQ＝8，PQ＝16，
△QCH逆时针选在120°得到△QC'G，则∠BQC'＝60°，
∵S矩形ABCD＝2S△BCP＝2（S△四边形GQHP+S△BQC'）＝2（64+S△BQC'），
设△BC'Q的外接圆半径为r，
∵∠BQC'＝60°，GQ＝8，
∴外接圆的圆心O在GQ上时，BC'的长最小，
∴r＝2（8﹣r），
解得，
，
∴S△BQC'的最小值，
∴S矩形ABCD的最小值为．