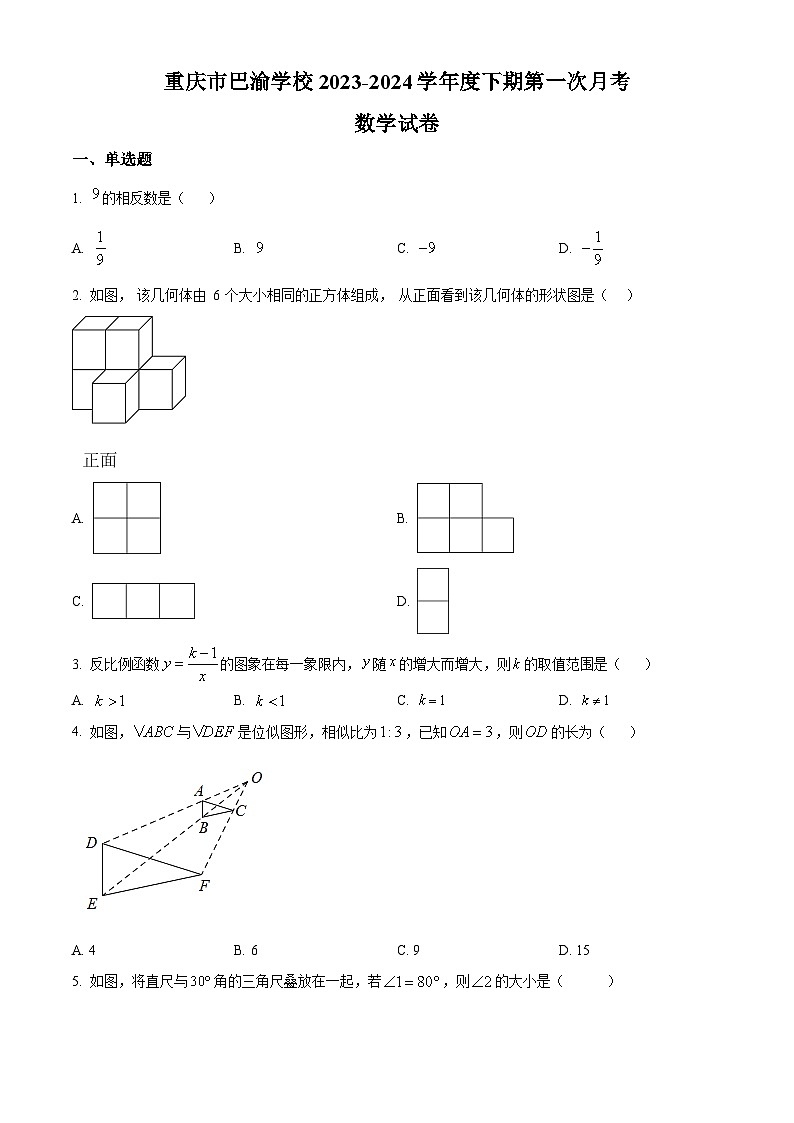





重庆市巴渝学校2023-2024学年九年级下学期第一次月考数学试题(原卷版+解析版)
展开
这是一份重庆市巴渝学校2023-2024学年九年级下学期第一次月考数学试题(原卷版+解析版),文件包含精品解析重庆市巴渝学校2023-2024学年九年级下学期第一次月考数学试题原卷版docx、精品解析重庆市巴渝学校2023-2024学年九年级下学期第一次月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
一、单选题
1. 的相反数是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了相反数即只有符号不同的两个数,熟练掌握定义是解题的关键.根据只有符号不同的两个数互为相反数判断即可.
【详解】的相反数是.
故选:C.
2. 如图, 该几何体由 6 个大小相同正方体组成, 从正面看到该几何体的形状图是( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用从正面看到的图形叫做主视图,根据图中5个正方体的摆放位置即可判定.
【详解】解:从正面看,主视图有3列,正方形的数量分别为:2、2、1,
故选B.
【点睛】本题考查了简单组合体的三视图,正确把握观察角度得出正确视图是解题的关键.
3. 反比例函数的图象在每一象限内,随的增大而增大,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据反比例函数的增减性可得出,再求出k的范围即可.
【详解】解:∵反比例函数的图象在每一象限内,y随x的增大而增大,
∴,
解得,
故选B.
【点睛】本题考查了反比例函数的图象和性质,解题的关键是熟记:对于反比例函数,当时,在每一象限内,随的增大而减小;反之,当时,在每一象限内,随的增大而增大.
4. 如图,与是位似图形,相似比为,已知,则的长为( )
A. 4B. 6C. 9D. 15
【答案】C
【解析】
【分析】由与是位似图形,位似比为,可得,继而可求得的长.
【详解】∵与是位似图形,相似比为1:3,
∴,且,
∵,
∴,
∵,
∴,
故选:C.
【点睛】本题主要考查了位似图形性质,平行线分线段成比例,掌握位似图形的性质是解答本题的关键.
5. 如图,将直尺与角的三角尺叠放在一起,若,则的大小是( )
A. B. C. D.
【答案】A
【解析】
【分析】如图,先利用平角求出∠4,再利用两直线平行,同位角相等即可求解.
【详解】解:如图所示;
,,
,
,
.
即的大小是40°.
故选:A.
【点睛】本题主要考查平行线的性质,熟练掌握平行线的性质是解决问题的关键.
6. 估计的值应在( )
A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间
【答案】C
【解析】
【分析】此题主要考查了估算无理数的大小,先利用二次根式的混合运算法则计算,进而估算的取值范围,进而得出答案.
【详解】解:,
∵,
∴,
∴的值在3和4之间,
故选:C.
7. 如图,是由大小相同的小五角星按照一定的规律排列而成的图形,观察图中的规律,则第n个图形的小五角星的个数为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据已知图形中的小五角星个数,得出第n个图形中五角星个数为4+n(n+1).
【详解】解:第1 个图形有个小五角星,
第2个图形有个小五角星,
第3个图形有个小五角星,
第4个图形有个小五角星,
第个图形有个小五角星.
故选D.
【点睛】本题主要考查图形的变化规律,解题的关键是将已知图形分割成两部分,并从中找到总个数的通项公式4+n(n+1).
8. 如图,是的直径,,是的弦,是的切线,为切点,与交于点.若点为的中点,,则的度数为( )
A. B. C. D.
【答案】C
【解析】
【分析】如图:连接,根据切线的性质得到,根据直角三角形的性质求出,由点为的中点可得,最后等腰三角形的性质及三角形内角和定理即可解答.
【详解】解:如图:连接,
∵是的切线,
∴,
∴,
∵,
∴,
∵点为的中点,
∴,
∵,
∴,
故选:C.
【点睛】本题主要考查了圆的切线的性质、圆周角定理、等腰三角形的性质等知识点,灵活运用相关知识成为解答本题的关键.
9. 如图,点E在边长为4的正方形ABCD的CD边上,连接BE,将△BCE沿直线BE翻折,点C的对应点为C′,延长BC′交AD边于点F,若AF=3,则tan∠CBE的值为( )
A. B. C. D. 2
【答案】A
【解析】
【分析】连接,勾股定理求得,进而根据折叠的性质求得,进而求得,可得,证明,即可得点为的中点进而求得,根据正切的意义即可求得tan∠CBE的值
【详解】解:连接,
正方形ABCD的边长为4,
,,
AF=3,
,
,
折叠,
,,,
,
,
在与中,
,
,
,
,
故选:A.
【点睛】本题考查了求正切值,正方形的性质,折叠问题,勾股定理,求得为的中点是解题的关键.
10. 有依次排列的3个整式:x,,,对任意相邻的两个整式,都用右边的整式减去左边的整式,所得之差写在这两个整式之间,可以产生一个新整式串:x,7,,,,则称它为整式串1;将整式串1按上述方式再做一次操作,可以得到整式串2;以此类推通过实际操作,得出以下结论:
①整式串2为:x,,7,x,,,,,;
②整式串3的和为;
③整式串3的所有整式的和比整式串2的所有整式的和小2;
④整式串2022的所有整式的和为;
上述四个结论正确的有( )个
A. 1B. 2C. 3D. 4
【答案】C
【解析】
【分析】根据整式的加减运算法则进行计算,从而得出规律进行求解.
【详解】解:∵第一次操作后的整式串为:,,,,,共个整式,
第一次操作后的整式串的和为: ,
∴第二次操作后的整式串为,,,,,,,,,共个整式,故①的结论正确,符合题意;
第二次操作后所有整式的和为: 第三次操作后整式串为,,,,,,,,,,,,,,,,,共个整式,
第三次操作后整式串的和为:
,故②的结论正确,符合题意;
故第三次操作后的整式串的和与第二次操作后的整式和的差为:,即整式串的所有整式的和比整式串的所有整式的和小,故结论正确,符合题意;
…
∴第次操作后所有整式的积为,
∴第次操作后,所有的整式的和为,故的说法不正确,不符合题意;
正确的说法有①②③,共个.
故选:C.
【点睛】本题主要考查了整式的加减计算,数字类的规律探索,解题关键是从所给的式子分析出所存在的规律.
二、填空题
11. 计算:________.
【答案】1
【解析】
12. 如果一个正边形的每个内角为,那么这个正边形的边数为_____.
【答案】5
【解析】
【分析】根据多边形的内角和公式列出算式,计算即可.
【详解】解:解:由题意得,解得,,
解得:,
故答案为:5.
【点睛】本题考查的是正多边形的内角问题,掌握多边形的内角和公式是解题的关键.
13. 一个不透明的口袋中有三张卡片,上面分别写有数字1,2,3,除数字外三张卡片无其他区别,现从中随机抽取两张卡片,则卡片上的数字之和是奇数的概率是_____.
【答案】
【解析】
【分析】列表求出所有出现的情况数,再根据概率公式即可得出答案.
【详解】解:根据题意列表如下:
共有6种情况,则卡片上的数字之和是奇数的情况有4种,
故卡片上的数字之和是奇数的概率是.
故答案为:.
【点睛】此题考查了列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件,用到的知识点为:概率=所求情况数与总情况数之比.
14. 某网购平台2014年“双11”交易额为571亿元,该平台2016年“双11”交易额为1207亿元,为求2014年到2016年的年平均增长率(设为),可列方程为____________.
【答案】
【解析】
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.设这两年的年平均增长率为,利用该平台2016年“双11”交易额2014年“双11”交易额(1+这两年的年平均增长率为)2,,可列出关于的一元二次方程,即可得出结论.
【详解】解:设这两年的年平均增长率为,
根据题意得:.
故答案为:.
15. 已知如图,在中,,,以C为圆心为半径作弧,交的延长线于点E,以B为圆心为半径交的延长线于点D,若,则阴影部分的面积是________.
【答案】##0.5
【解析】
【分析】本题主要考查了求扇形面积,勾股定理,根据计算,即可得出答案.
【详解】在中,,,
∴,
∴.
根据勾股定理,得.
.
故答案为:.
16. 如图,△ABC中,点D为边BC的中点,连接AD,将△ADC沿直线AD翻折至△ABC所在平面内,得△ADC′,连接CC′,分别与边AB交于点E,与AD交于点O.若AE=BE,AD=6,则BC′的长为________.
【答案】4
【解析】
【分析】根据得到∠=90°,根据折叠的性质,得到∠AOE=∠DOC=90°,从而证明DO是中位线,△AOE≌△,从而得到AD=AO+DO=,代入计算即可.
【详解】∵点D为边BC的中点,△ADC沿直线AD翻折得△ADC′,
∴,∠AOE=∠DOC=90°,
∴∠=90°,∥OD,
∴,
∵BD=DC,
∴,
∴DO是△的中位线,
∴,
∵AE=BE,∠=∠AOE=90°,∠=∠AEO,
∴△AOE≌△,
∴,
∴AD=AO+DO=,
∴,
解得,
故答案为:4.
【点睛】本题考查了折叠的性质,三角形全等的判定和性质,三角形中位线定理,直角三角形的判定,熟练掌握中位线定理,三角形全等的判定和性质是解题的关键.
17. 若数 使关于 的一元一次不等式组 的解集是,且使关于 的分式方程有非负整数解,则符号条件的所有整数的值之和为_____________.
【答案】6
【解析】
【分析】此题主要考查不等式组与分式方程的求解综合,先根据不等式组的解集为求出m的取值,再根据分式方程有非负整数解得到m的取值,故可得到符合条件的所有整数m的值,即可求解.
【详解】解
由①得,
由②得,
∵解集是,
∴,
解,
去分母得,
解得y=,
∵有非负整数解,
∴且,
∴且,
解得,且,
∴且,
∵m为整数,为非负整数,
∴, 1,3,5,
故,
故答案为6.
18. 介绍一个“能被13整除的数的特征”的数学小知识:一个多位数(数位大于等于4)的末三位数与末三位数以前的数字所组成的数之差记为,如果能被13整除,则这个多位数就一定能被13整除.例如数字160485,这个数末三位是485,末三位以前是160,,.即325能被13整除,那么160485也能被13整除.则______;若,均为13的倍数,且,,(,,,且,,均为整数).规定,当时,的最大值为___________.
【答案】 ①. 126 ②.
【解析】
【分析】(1)直接根据公式代入求解即可得到答案;
(2)根据公式代入求出、,结合整除及取值范围即可得到答案;
【详解】解:由题意可得,
∵,
∴,
∵,,
∴,,
∴,
∵m是的倍数,且,
∴可以取或或或或或或,
∴可能是:、2、、、、、,
∵是整数,
∴,
∴,
∵,
∴,
∴,
∴,
∴①当时,,
②当时,,
③当时,,
④当时,,
⑤当时,,
∵
∴的最大值为,
故答案为:126,.
【点睛】本题考查新定义的运算及整除问题,解题的关键是正确理解新定义,根据的条件求出a.
三、解答题
19. 计算:
(1);
(2).
【答案】(1)
(2)
【解析】
【分析】本题考查了分式的混合运算,单项式乘多项式,以及完全平方公式等知识点,
(1)原式利用完全平方公式,以及单项式乘多项式法则计算,去括号合并即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
熟练掌握运算法则及公式是解本题的关键.
【小问1详解】
;
【小问2详解】
.
20. 如图,在四边形中,.
(1)用直尺和圆规完成以下基本作图:作线段的垂直平分线,分别交、、于点、、,连接、;在线段的延长线上取一点,使得,连接.(保留作图痕迹,不写作法和结论)
(2)在(1)所作图形中,证明:是等腰三角形(补全证明过程)
证明:平分,
,
,
,
在和中,
,
,
______②,
,
四边形为平行四边形,
垂直,
平行四边形为______③,
,
,
,
即:_____④,
是等腰三角形.
【答案】(1)见解析;
(2)①;②;③菱形;④.
【解析】
【分析】根据线段垂直平分线的作图方法作图,再以点为圆心,的长为半径画弧,交的延长线于点,连接,,即可.
根据全等三角形的判定与性质、平行四边形的判定、菱形的判定可得答案.
本题考查作图复杂作图、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质,熟练掌握全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质、线段垂直平分线的作法是解答本题的关键.
【小问1详解】
根据题意,画图如下:
.
【小问2详解】
证明:平分,
,
,
,
在和中,
,
,
.
,
四边形为平行四边形.
垂直,
平行四边形为菱形,
.
,
,
即:,
是等腰三角形.
故答案为:;;菱形;.
21. 为做好青少年毒品预防教育工作,某中学对本校初中七年级、八个年级的学生约3000名进行“珍爱生命,远离毒品”的专题教育,并举办了禁毒知识答题竞赛,学校在七年级、八年级各随机抽取了20份试卷进行分析、整理,其中七年级20名学生的成绩为:75,40,61,96,85,68,70,90,73,73,75,80,63,85,50,85,81,91,65,94.对这40份试卷的成绩按照五个等级(试卷满分为100分,学生得分均为整数)制成扇形统计图,并按年级制成了统计表.
等级说明:
A等:得分在90分及以上; B等:得分在80分~89分;
C等:得分在70分~79分; D等:得分在60分~69分
E等:低于60分.
抽查的七、八年级成绩统计表
请根据以上信息解答:
(1)a=___,b=___,c=___.
(2)你认为该校七、八年级中,哪个年级的竞赛成绩较好?请说明理由(说明一条即可);
(3)请你估算一下,本次竞赛七年级、八个年级的学生成绩达到80分及以上的学生大约有多少人?
【答案】(1)15,75,85
(2)八年级的竞赛成绩较好
(3)本次竞赛七年级、八个年级的学生成绩达到80分及以上的学生大约有1425人
【解析】
【分析】(1)将1-其它百分率求出a,把七年级20名学生成绩从小到大排序,根据中位数计算出b,根据众数定义求c即可;
(2)根据平均数相同,利用中位数和方差进行决策即可;
(3)用样本中80分以上的百分比×3000计算即可
【小问1详解】
解:a%=1-20%-27.5%-30%-7.5%=15%
∴a=15,
七年级20名学生的成绩从小到大排列为:40,50,61,63,65,68,70,73,73,75,75, 80,81, 85, 85, 85, 90, 91, 94. 96,
第10与第11两名学生的成绩都是75,
∴中位数b=75分,
重复次数最多的是85分,
∴众数为85分
∴c=85分
故答案为15,75,85;
【小问2详解】
解:两个年级的平均数都是75分相同,中位数上看八年级78分高于七年级75分,说明八年级75分以上多余七年级,从方差上看八年级方差151.5低于七年级方差200.8,
∴八年级的竞赛成绩较好;
【小问3详解】
解:被抽查80分以上百分率20%+27.5%=47.5%,
∴本次竞赛七年级、八个年级的学生成绩达到80分及以上的学生大约有3000×47.5%=1425人
【点睛】本题考查样本中的百分比,中位数,众数,利用集中趋势的量和离散趋势的量进行决策,利用样本的百分比含量估计总体中的数量,掌握样本中的百分比,中位数,众数,利用集中趋势的量和离散趋势的量进行决策,利用样本的百分比含量估计总体中的数量是解题关键.
22. “当你背单词时,阿拉斯加的鳕鱼正跃出水面;当你算数学时,南太平洋的海鸥正掠过海岸;当你晚自习时,地球的极圈正五彩斑斓;但少年,梦要你亲自实现,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现.”这是直播带货新平台“东方甄选”带货王董宇辉在推销鳕鱼时的台词.所推销鳕鱼的成本为每袋元,当售价为每袋元时,每分钟可销售袋. 为了吸引更多顾客,“东方甄选”采取降价措施.据市场调查反映:销售单价每降元,则每分钟可多销售袋.
(1)每袋鳕鱼的售价为多少元时,每分钟的销量为袋?
(2)“东方甄选”不忘公益初心,热心教育事业,其决定从每分钟利润中捐出元帮助留守儿童,为了保证捐款后每分钟利润达到元,且要最大限度让利消费者,求此时鳕鱼的销售单价为多少元?
【答案】(1)每袋鳕鱼的售价为元时,每分钟的销量为袋.
(2)鳕鱼的销售单价为元.
【解析】
【分析】本题考查一元一次方程和一元二次方程的应用,解题的关键是根据题意,找到等量关系,列出方程,进行解答.
(1)设每袋鳕鱼的售价为元,根据题意,则,解出,即可;
(2)设此时鳕鱼的销售单价为元,根据题意,则方程为,解出方程,即可.
【小问1详解】
解:设每袋鳕鱼的售价为元,每分钟的销售量为袋,
∴,
解得:,
答:每袋鳕鱼的售价为元时,每分钟的销售量为袋.
【小问2详解】
解:设此时鳕鱼的销售单价为元,
∴,
解得:,,
∵要最大限度让利消费者,
∴,
答:此时鳕鱼的销售单价为元.
23. 如图,四边形是边长为4的正方形,O是正方形的中心,动点P从点A出发沿折线A→B→C方向运动,到达C点停止,在上的运动速度为每秒1个单位长度,在上的运动速度为每秒2个单位长度,设运动时间为t秒,的面积为y.
(1)请直接写出y关于t的函数表达式并注明自变量t的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出的面积为3时t的值.
【答案】(1)
(2)图见解析,当时,y随t的增大而减小;
(3)或
【解析】
【分析】本题考查了一次函数在实际问题中的应用,掌握函数的解析式求解、函数图象、数形结合的数学思想是解题关键.
(1)分类讨论、两种情况,画出对应的图形即可求解;
(2)描点、连线即可完成作图;
(3)作出直线,确定其与函数图象的交点横坐标即可求解.
【小问1详解】
解:①当时,动点P在上运动,
作,如图所示:
∵,
∴
∵O是正方形的中心,
∴
∴;
②当时,动点P在上运动,
作,如图所示:
此时,
∵O是正方形的中心,
∴
∴;
综上所述:
【小问2详解】
:如图所示:
当时,y随t的增大而减小
【小问3详解】
解:作出直线,如图所示:;
可知直线与函数的图象的交点横坐标为和
∴的面积为3时,或
24. 仙女山大草原部分景点的道路分布如图所示,其中是骑行公路.经测量,点C在点B正南方,点D在点B正东方,,米,点A在点B的北偏西23°方向,米,点E在点D正北方且在点A正东方.(参考数据:,,,)
(1)求的距离;(结果精确到个位)
(2)小华和小亮同时从游客中心点C出发,前往点E处的露营基地,小华沿路线步行到达基地,速度为;小亮以的速度沿到达点A后,立即骑行到达点E,骑行速度为,请计算说明小华和小亮谁先到达E点?
【答案】(1)的距离约为550米
(2)小亮先到达E点
【解析】
【分析】本题考查的是解直角三角形的实际应用,作出合适的辅助线构建直角三角形是解本题的关键.
(1)设的延长线交于点F,可得和都是直角三角形,四边形是矩形,,再利用锐角三角函数求解即可;
(2)在中,求解米,在中,求解米,再进一步求解即可.
【小问1详解】
解:设的延长线交于点F,
由题意知:和都直角三角形,四边形是矩形,,
在中,
∵,米,
∴(米),
∴米,
∴在中,
∵,米,
∴(米),
∴(米),
答:的距离约为550米;
【小问2详解】
在中,
∵,米,
∴(米),
∴在中,
∵,米,
∴(米),
∴米,
∴小华到达E点所花时间为,
小亮到达E点所花时间为,
∵,
∴小亮先到达E点.
25. 如图1,在平面直角坐标系中,抛物线与轴交于、两点,与轴交于点,连接、.
(1)求抛物线的函数表达式;
(2)点是抛物线上位于直线下方一动点,过点作轴的平行线交直线于点,过点作的平行线交轴于点,求的最大值及此时点的坐标;
(3)如图2,点是抛物线上一点,连接,当线段的中点恰好在轴上时,探究抛物线上是否存在点,使.若存在,请直接写出点的坐标,若不存在,请说明理由.
【答案】(1)
(2)有最大值为,此时点,;
(3)存在,点的坐标为:或.
【解析】
【分析】(1)设抛物线的表达式为:,用待定系数法即可求解;
(2)证明,即可求解;
(3)当时,则,即可求解.
【小问1详解】
抛物线与轴交于、两点,
设抛物线的表达式为:,
将代入得:
则,
解得:,
则抛物线的表达式为:;
【小问2详解】
过点作轴于点,如图1,
由点、的坐标得,,
,则,
则,
设直线的表达式为:,
将、代入得,
,解得:,
所以直线表达式为:,
设点,则点,
则,
,
则有最大值为,此时点,;
【小问3详解】
存在,理由:
如图2,当线段的中点恰好在轴上时,由中点坐标公式得:,
即点,
设直线交于点,
设点,
当时,
则,
即,
解得:,
即点,
由点、的坐标得,直线的表达式为:,
联立直线和抛物线的表达式得:
解得:(舍弃)或,
当和平行时,直线的解析式为:,
与抛物线解析式联立可求的坐标为:.
即点的坐标为:或.
【点睛】本题考查的是二次函数综合运用,涉及到解直角三角形、一次函数的性质、等腰三角形的性质等,综合性强,难度适中.
26. 在中,,,点D为边上一动点,连接,将绕着D点逆时针方向旋转得到,连接.
(1)如图1,,点D恰好为中点,与交于点G,若,求的长度;
(2)如图2,与交于点F,连接,在延长线上有一点P,,求证:;
(3)如图3,与交于点F,且平分,点M为线段上一点,点N为线段上一点,连接、,点K为延长线上一点,将沿直线翻折至所在平面内得到,连接,在M、N运动过程中,当取得最小值,且时,请直接写出的值.
【答案】(1);
(2)证明见解析; (3)
【解析】
【分析】(1)由勾股定理,得到,根据等腰三角形三线合一的性质可知,点是的中点,得到,从而得到,再由勾股定理,求得,由旋转的性质可知,,,最后利用勾股定理,即可求出的长度;
(2)过点作交于点,由题意可知,是等腰直角三角形,进而得出,,利用旋转的性质,易证,得到,,进而证明,推出,即可证明结论;
(3)在上取点,使得,连接,根据旋转性质和角平分线的定义,易证,得到,进而推出当、、三点共线,且时,取得最小值,再根据折叠的性质和三角形外角的定义,得出、、三点共线,,进而得到,最后分别表示出,,即可求出的值.
【小问1详解】
解:,,
,
,
点是的中点,
,
点D为中点,
,
在中,,
由旋转的性质可知,,,
;
【小问2详解】
证明:如图2,过点作交于点,
,
,,
是等腰直角三角形,
,
,
,,
由旋转的性质可知,,,
,
,
在和中,
,
,
,,
,
在和中,
,
,
,
,
;
【小问3详解】
解:如图3,在上取点,使得,连接,
由旋转的性质可知,,,
是等腰直角三角形,
平分,
,
在和中,
,
,
,
,
当、、三点共线,且时,取得最小值,如图,
由旋转的性质可知,,,
,
,
将沿直线翻折至所在平面内得到,
,,,
,
,
,
,
,
,
,即、、三点共线,
,
,,
,
,
,,
,
,
,
【点睛】本题考查了勾股定理,等腰三角形的判定和性质,直角三角形的特征,旋转的性质,全等三角形的判定和性质,折叠的性质,三点共线问题等知识,灵活运用相关知识解决问题是解题关键.第一张
第二张
1
2
3
1
3
4
2
3
5
3
4
5
七年级
八年级
平均数
75
75
中位数
b
78
众数
c
74
方差
200.8
151.5
相关试卷
这是一份重庆市梁平区梁平区福德学校2023-2024年八年级下学期第一次月考数学试题(原卷版+解析版),文件包含精品解析重庆市梁平区梁平区福德学校2023-2024年八年级下学期第一次月考数学试题原卷版docx、精品解析重庆市梁平区梁平区福德学校2023-2024年八年级下学期第一次月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
这是一份重庆市梁平区梁平区福德学校2023-2024学年七年级下学期第一次月考数学试题(原卷版+解析版),文件包含精品解析重庆市梁平区梁平区福德学校2023-2024学年七年级下学期第一次月考数学试题原卷版docx、精品解析重庆市梁平区梁平区福德学校2023-2024学年七年级下学期第一次月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
这是一份重庆市渝北中学校2023-2024学年九年级下学期第一次月考数学试卷,共8页。试卷主要包含了 作图请用黑色2B铅笔或0, 参考公式等内容,欢迎下载使用。









