





适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数第1节函数的概念及其表示课件新人教A版
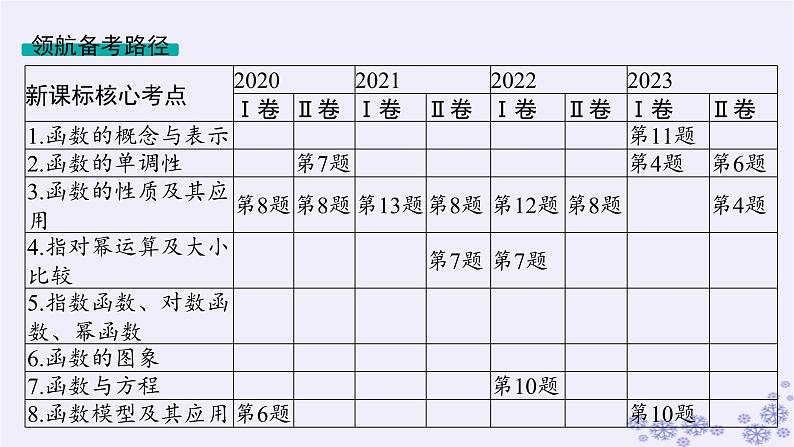
展开考情分析:1.函数模块是高考考查的核心内容之一,主要以基本初等函数或者基本初等函数组成的复合函数为载体,考查定义域、值域、性质、图象、零点等相关知识,近几年高考对抽象函数考查的频率明显增加,重点考查函数的奇偶性、周期性与单调性等,常与导数、不等式、方程等交汇命题,考查数形结合、分类讨论、函数与方程等数学思想,以客观题的形式出现,难度中等,分值5~10分.2.高考对函数知识的考查,重在交汇融合,还多有隐性考查,渗透在整卷的考查中.
复习策略:1.明晰重要概念,熟练掌握常见基本初等函数的图象与性质:定义域、值域、最值、奇偶性、周期性、单调性、零点等概念是解决函数问题的基础,应明确;二次函数、指对幂函数的图象与性质贯穿在解决函数问题的全过程,应熟练掌握.2.强化数学思想方法的训练:数形结合、函数与方程、分类讨论等数学思想方法在解决函数问题中具有重要应用,应强化应用意识.3.注重数学运算能力的提升:解决函数问题的过程中,代数推理、变形化简、数值计算等贯穿其中,是影响解题成败的关键因素,因此在复习中应重视运算能力的训练与提升.4.善于运用函数性质的二级结论快速、简洁地解决相关问题.5.涉及抽象函数问题,注意寻找函数原型帮助分析和解决问题.
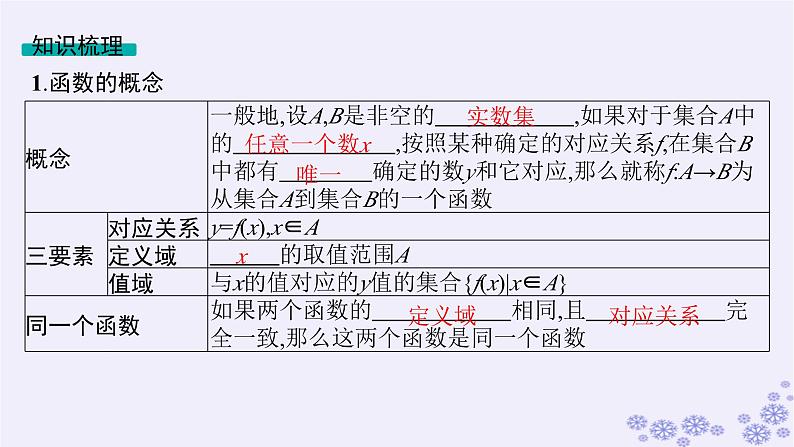
1.了解构成函数的要素,能求简单函数的定义域.2.理解函数的三种表示方法:图象法、列表法、解析法.会根据不同的需要选择恰当的方法.3.通过具体实例,了解简单的分段函数,并能简单应用.
微思考定义域与值域相同的两个函数一定是同一个函数吗?值域与对应关系相同的两个函数一定相等吗?
提示 不一定是同一个函数.如函数y=3x和y=2x-1,二者的定义域均为R,值域也均为R,但两个函数不同.值域与对应关系相同的两个函数也不一定相等.如函数y=x2,x∈[0,2)和函数y=x2,x∈(-1,2),两函数解析式相同,值域也相同,但定义域不同,所以不是相等函数.
2.函数的表示方法表示函数的常用方法有 、图象法、列表法. 微思考直线x=a(a为常数)与函数f(x)的图象的交点个数是多少?
提示 直线x=a(a为常数)与函数f(x)的图象的交点个数是1或0.若设f(x)的定义域为D,则当a∈D时,有1个交点,当a∉D时,有0个交点.
3.分段函数如果一个函数,在其定义域内,对于自变量的不同取值区间,有不同的对应方式,则称其为分段函数.
微点拨1.分段函数只是在定义域的不同区间上解析式不同,但它表示的是同一个函数.2.分段函数的定义域是各段区间的并集,值域是各段值域的并集.3.分段函数定义域的各段区间的交集一定是空集.4.解析式中含有绝对值的函数一般都可以化为分段函数.5.分段函数的图象中,横坐标相同的地方不能有两个或两个以上的点.
常用结论常见函数的定义域如下:(1)分式中分母不能等于0;(2)偶次根式的被开方数大于或等于0;(3)零次幂的底数不能为0;(4)一次函数、二次函数、指数函数y=ax(a>0,a≠1)、正弦函数y=sin x、余弦函数y=cs x的定义域均为R;(5)对数函数y=lgax(a>0,a≠1)的定义域为(0,+∞);
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.对于函数f:A→B,其值域是集合B.( )
题组二回源教材5.(人教B版必修第一册3.1.1节练习B第8题)已知函数f(x+1)=2x-3,求f(4),f(x).
解 令x+1=4,解得x=3,代入得f(4)=3;设x+1=t,则x=t-1,代入得f(t)=2t-5,因此f(x)=2x-5.
6.(人教A版必修第一册74页习题3.1第17题)探究是否存在函数f(x),g(x)满足条件:(1)定义域相同,值域相同,但对应关系不同;(2)值域相同,对应关系相同,但定义域不同.
解 (1)存在,例如f(x)=2x+1与g(x)=3x-1的定义域和值域均为R,但对应关系不同.(2)存在,例如f(x)=x2,x∈R与g(x)=x2,x∈[0,+∞)的值域和对应关系相同,但定义域不同.
(-∞,0)∪(0,1]
考点一函数的概念及应用
例1(1)(多选题)(2024·浙江衢州模拟)已知函数f(x)与g(x),若存在f(x)使得f(g(x))=x2,则g(x)不可能为( )A.x2-2 023xB.sin xC.2x-1D.|x|
解析 对于A选项,若g(x)=x2-2 023x,当x=0时,f(0)=0,当x=2 023时,f(0)=2 0232,相当于1个x值对应两个y值,不符合函数定义,即A错误;对于B选项,取x=0和x=π,有f(g(0))=f(0)=0,f(g(π))=f(0)=π2,不符合函数定义,所以B
(2)(2024·浙江宁波模拟)已知函数f(x)满足:对任意的非零实数x,y,都有f(x+y)=( )f(x)f(y)成立,且f(1)=2,若f(n)=f(n+1),n∈Z,n≠0,则n=( )A.-3B.-2C.2D.3
[对点训练1](多选题)(2024·广东深圳模拟)下列式子中,不存在函数f(x)使其对任意x∈R都成立的是( )A.f(x)=xB.f(sin x)=xC.f(cs x)=xD.f(sin x)=cs x
解析 对于A,对任意x∈R,f(x)=x都成立;对于B,取x=0和x=π,得到f(0)=0,
函数的定义;对于D,取x=0和x=π,得到f(0)=1,f(0)=0,不符合函数的定义,故选BCD.
解析 要使函数有意义,应满足 解得-1
(2)(2024·河北衡水中学检测)已知函数y=f(x)的定义域为[0,4],则函数 的定义域是( )A.(1,5]B.(1,2)∪(2,5)C.(1,2)∪(2,3]D.(1,3]
例3根据下列条件求函数的解析式:(1)已知f(x)是一次函数,且满足3f(x)-2f(x-1)=2x+5,求f(x)的解析式;(2)已知函数f(x)满足f(cs x-1)=cs 2x-1,求f(x)的解析式;
解 (1)依题意设f(x)=ax+b(a≠0),则由3f(x)-2f(x-1)=2x+5可得3(ax+b)-2[a(x-1)+b]=2x+5,
(2)函数f(x)满足f(cs x-1)=cs 2x-1=2cs2x-1-1=2cs2x-2,设cs x-1=t,则cs x=t+1,由cs x∈[-1,1]知t∈[-2,0],故原函数可转化为f(t)=2(t+1)2-2 =2t2+4t,t∈[-2,0],即f(x)的解析式为f(x)=2x2+4x(-2≤x≤0).
(4)已知f(x)+2f(-x)=x2+2x,求f(x)的解析式.
立,故函数f(x)的解析式为f(x)=x2-2(x≥2).
(4)因为f(x)+2f(-x)=x2+2x,①所以f(-x)+2f(x)=x2-2x,所以2f(-x)+4f(x)=2x2-4x,②
考点四分段函数(多考向探究预测)
考向1分段函数的求值问题
例4(1)(2024·广西南宁模拟)已知函数f(x)= 那么f(f(-1))=( )A.7B.6C.5D.4
解析 因为f(x)= 所以f(-1)=-(-1)+1=2,所以f(f(-1))=f(2)=22=4,故选D.
(2)(2024·陕西安康模拟)已知函数f(x)= 则f(lg23)= .
(3)(2024·北京海淀区模拟)已知函数f(x)= 若f(m)=-1,则实数m的值为 .
考向2分段函数与不等式例5(2024·浙江嘉兴模拟)设函数f(x)= 若f(a)≥0,则实数a的取值范围是 .
(-∞,-2]∪[0,+∞)
解析 当a≤0时,f(a)=a2+2a,由f(a)≥0,得a2+2a≥0,解得a≥0或a≤-2,又因为a≤0,所以得a=0或a≤-2;当a>0时,f(a)=lg(a2+1),由f(a)≥0得lg(a2+1)≥0,解得a∈R,又因为a>0,所以得a>0.综上,实数a的取值范围是(-∞,-2]∪[0,+∞).
变式探究1 (变条件)本例中,函数解析式不变,将“f(a)≥0”改为“f(a-1)≤3”,则实数a的取值范围是 .
解析 当a-1≤0即a≤1时,f(a-1)=(a-1)2+2(a-1),由f(a-1)≤3得(a-1)2+2(a-1) ≤3,解得-2≤a≤2,又因为a≤1,所以得-2≤a≤1;当a-1>0即a>1时,f(a-1)
变式探究2(变条件)本例中,函数解析式不变,将“f(a)≥0”改为“f(f(m))<0”,则实数m的取值范围是 .
解析 令f(m)=t,则“f(f(m))<0”即为“f(t)<0”.当t≤0时,f(t)=t2+2t,由f(t)<0得t2+2t<0,解得-2
适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式第3节二次函数及其性质课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第2章一元二次函数方程和不等式第3节二次函数及其性质课件新人教A版,共36页。PPT课件主要包含了强基础固本增分,研考点精准突破,目录索引,题组三连线高考,考点二二次函数的图象,ABD,-∞-2等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第1章集合与常用逻辑用语课时规范练1集合课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第1章集合与常用逻辑用语课时规范练1集合课件新人教A版,共16页。PPT课件主要包含了x1≤x≤4等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第1章集合与常用逻辑用语第2节常用逻辑用语课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第1章集合与常用逻辑用语第2节常用逻辑用语课件新人教A版,共43页。PPT课件主要包含了强基础固本增分,研考点精准突破,目录索引,全称量词,存在量词,2+∞,BCD等内容,欢迎下载使用。












