





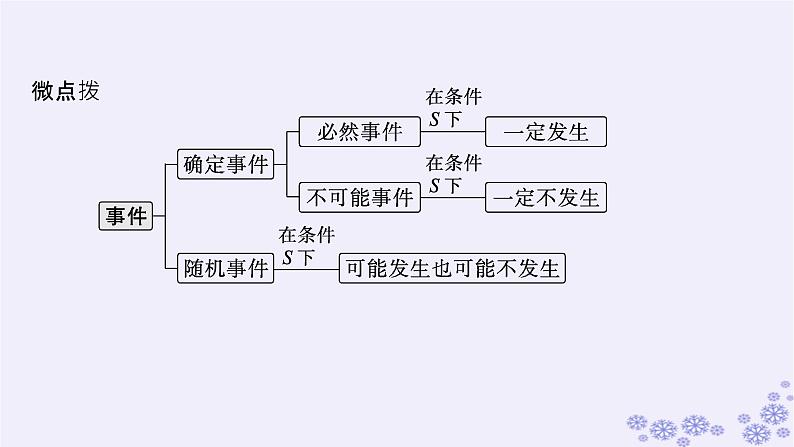
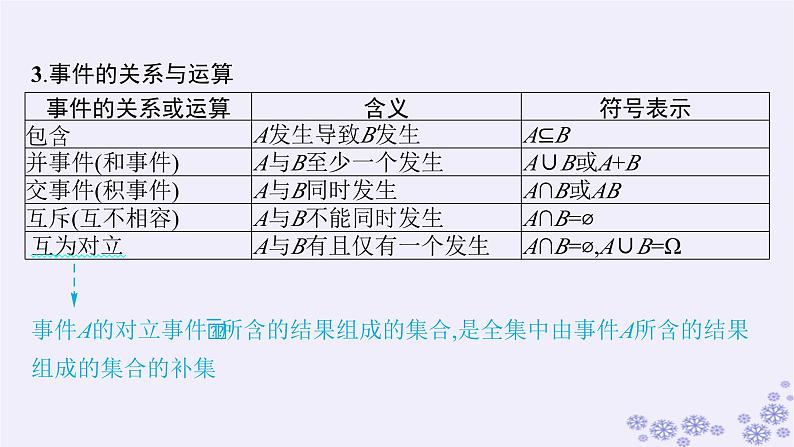
适用于新高考新教材备战2025届高考数学一轮总复习第11章计数原理概率随机变量及其分布第4节随机事件的概率与古典概型课件新人教A版
展开1.结合具体实例,理解样本点和有限样本空间的含义,理解随机事件与样本点的关系.2.了解随机事件的并、交与互斥的含义,能结合实例进行随机事件的并、交运算.3.理解古典概型,能计算古典概型中简单随机事件的概率.4.理解概率的性质,掌握随机事件概率的运算法则.5.会用频率估计概率.
1.样本点和样本空间(1)定义:我们把随机试验E的每个可能的 称为样本点,全体样本点的集合称为试验E的 . (2)表示:一般地,我们用Ω表示样本空间,用ω表示样本点.如果一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
3.事件的关系与运算
事件A的对立事件 所含的结果组成的集合,是全集中由事件A所含的结果组成的集合的补集
微点拨定义多个事件的和事件以及积事件.例如,对于三个事件A,B,C,A∪B∪C(或A+B+C)发生当且仅当A,B,C中至少一个发生,A∩B∩C(或ABC)发生当且仅当A,B,C同时发生.
4.频率与概率(1)定义一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.因此,我们可以用 来估计概率 .
从数量上反映了随机事件发生的可能性的大小
微点拨理解频数与频率需注意:(1)前提:对于给定的随机事件A,在相同的条件S下重复n次试验,观察事件A是否出现.(2)频数:指的是n次试验中事件A出现的次数nA.频率:指的是事件A出现的比例fn(A)= .
(2)概率的基本性质性质1:对任意的事件A,都有P(A) ; 性质2:必然事件的概率为1,不可能事件的概率为0,即P(Ω)= ,P(⌀)= ; 性质3:如果事件A与事件B互斥,那么P(A∪B)= ; 性质4:如果事件A与事件B互为对立事件,那么P(B)= ,P(A)= ; 性质5:如果A⊆B,那么 ,由该性质可得,对于任意事件A,因为⌀⊆A⊆Ω,所以0≤P(A)≤1; 性质6:设A,B是一个随机试验中的两个事件,有P(A∪B)= .
P(A)+P(B)-P(A∩B)
微思考概率与频率有什么区别?
提示 (1)概率是一个确定的数,是客观存在的,与试验次数无关,它度量该事件发生的可能性;(2)频率本身是随机的,在试验前不能确定,做同样次数的重复试验得到的事件的频率不一定相同;(3)频率是概率的近似值,在实际问题中,仅当试验次数足够多时,频率可近似地看作概率.
5.古典概型(1)具有以下两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.①有限性:样本空间的样本点只有 ; ②等可能性:每个样本点发生的可能性 .
判断一个试验是否是古典概型的关键点
(2)古典概型的概率公式一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A包含其中的k个样本点,则定义事件A的概率P(A)= .其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
常用结论如果事件A1,A2,…,An两两互斥:(1)事件A1∪A2∪…∪An发生的概率等于这n个事件分别发生的概率之和,即P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.对立事件一定互斥,但互斥事件不一定对立.( )2.“在适宜条件下,种下一粒种子观察它是否发芽”属于古典概型,其基本事件是“发芽与不发芽”.( )3.掷一枚硬币两次,出现“两个正面”“一正一反”“两个反面”,这三个结果是等可能事件.( )4.从市场上出售的标准为500±5 g的袋装食盐中任取一袋测其重量,属于古典概型.( )
题组二回源教材5.(人教A版必修第二册习题10.1第3题改编)抛掷两枚质地均匀的硬币,设事件A=“第一枚硬币正面朝上”,事件B=“第二枚硬币反面朝上”.下列结论中正确的是( )A.A与B互为对立事件B.A与B互斥C.A与B相等D.P(A)=P(B)
6.(人教A版必修第二册10.1.3节例8改编)先后抛掷一枚质地均匀的骰子2次,观察向上的点数,则点数和为5的概率是 .
解析 根据题意可得,基本事件总数为6×6=36个,其中点数和为5的有(1,4),(4,1),(2,3),(3,2)共4个样本点.∴出现向上的点数和为5的概率为
7.(人教A版必修第二册10.1.4节例11改编)从不包含大小王牌的52张扑克牌中随机抽取一张,设事件A=“抽到红心”,事件B=“抽到方片”,P(A)=P(B)= ,设C=“抽到红花色”,则P(C)= ;设D=“抽到黑花色”,则P(D)= .
题组三连线高考8.(2020·全国Ⅰ,文4)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
解析 由题意知一共有10种取法,当选A,O,C和B,O,D时符合要求,故
9.(2023·全国乙,文9)某学校举办作文比赛,共设6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题的概率为( )
解析 甲、乙两位同学各随机抽取一个主题,共有6×6=36种结果,而甲、乙两位同学抽到同一个主题的结果有6种,所以甲、乙两位同学抽到不同主
考点一 随机事件(多考向探究预测)
考向1随机事件间关系的判断例1(1)(多选题)对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A={两次都击中飞机},B={两次都没击中飞机},C={恰有一弹击中飞机},D={至少有一弹击中飞机},下列关系正确的有( )A.A⊆DB.B∩D=⌀C.A∪B=B∪DD.A∪C=D
解析 用(x1,x2)表示试验的射击情况,其中x1表示第1次射击的情况,x2表示第2次射击的情况,1表示击中,0表示没击中,则样本空间Ω={(0,0),(0,1),(1,0),(1,1)}.由题意得,A={(1,1)},B={(0,0)},C={(0,1),(1,0)},D={(0,1),(1,0),(1,1)}.则A⊆D,A∪C=D,且B∩D=⌀.即A,B,D正确;又B∪D=Ω,A∪B={(0,0),(1,1)}≠Ω,∴A∪B≠B∪D.故C错误.
(2)(多选题)(2024·山西朔州高三开学考试)从1,2,3,…,9中任取三个不同的数,则在下述事件中,是互斥但不是对立事件的有( )A.“三个都为偶数”和“三个都为奇数”B.“至少有一个奇数”和“至多有一个奇数”C.“至少有一个奇数”和“三个都为偶数”D.“一个偶数两个奇数”和“两个偶数一个奇数”
解析 从1~9中任取三个数,按这三个数的奇偶性分类,有四种情况:①三个均为奇数;②两个奇数一个偶数;③一个奇数两个偶数;④三个均为偶数,所以选项A,D是互斥但不是对立事件,选项C是对立事件,选项B不是互斥事件.故选AD.
考向2计算简单随机事件的频率与概率例2如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
(1)试估计40分钟内不能赶到火车站的概率;(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
解 (1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44(人),用频率估计相应的概率为P= =0.44.
(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率为
(3)设事件A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站;B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.结合(2)中表格知P(A1)=0.1+0.2+0.3=0.6,P(A2)=0+0.1+0.4=0.5.∵P(A1)>P(A2),∴甲应选择L1.同理,P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0+0.1+0.4+0.4=0.9.∵P(B1)
解析 因为A∪B表示“甲没有中奖或甲获得一等奖”,但甲还可能获得二等奖,即事件A和事件B不是对立事件,A错误;事件A表示“甲没有中奖”,事件C表示“甲中奖”,则事件A和事件C互斥且和事件为全集,所以事件A和事件C是对立事件,B正确;又因为B⊆C,所以P(B+C)=P(C),C选项正确;P(BC)=P(B),D选项错误.故选BC.
(2)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
①记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;②记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;③求续保人本年度平均保费的估计值.
解 ①事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为 =0.55,故P(A)的估计值为0.55.②事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为 =0.3,故P(B)的估计值为0.3.③由所给数据得
调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.因此,续保人本年度平均保费的估计值为1.192 5a.
考点二 互斥事件与对立事件的概率
例3某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:(1)P(A),P(B),P(C);(2)1张奖券的中奖概率;(3)1张奖券不中特等奖且不中一等奖的概率.
(2)1张奖券中奖包含中特等奖或一等奖或二等奖.设“1张奖券中奖”这个事件为M,则M=A∪B∪C.
[对点训练2]经统计,在服务场所一个营业窗口等候的人数相应的概率如下:
求:(1)至多2人排队等候的概率是多少?(2)至少3人排队等候的概率是多少?
解 记“0人排队等候”为事件A,“1人排队等候”为事件B,“2人排队等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F彼此互斥.(1)记“至多2人排队等候”为事件G,则G=A∪B∪C,所以P(G)=P(A∪B∪C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)(方法一)记“至少3人排队等候”为事件H,则H=D∪E∪F,所以P(H)=P(D∪E∪F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.(方法二)记“至少3人排队等候”为事件H,则其对立事件为事件G,所以P(H)=1-P(G)=0.44.
例4(1)(2023·全国甲,文4)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为( )
解析 由题意,设高一年级2名学生为A,B,高二年级2名学生为C,D,从这4名学生中随机选2名组织校文艺汇演有AB,AC,AD,BC,BD,CD,共6种,这2名学生来自不同年级的组合有AC,AD,BC,BD,共4种,故所求的概率
(2)(2024·江西新余模拟)我国购买新能源汽车的家庭越来越多.某学校为方便驾驶新能源汽车的教职工充电,在停车场开展充电桩安装试点.如图,试点区域共有十个车位,安装了三个充电桩,每个充电桩只能给其南、北两侧车位中的一辆新能源汽车充电.现有3辆燃油车和2辆新能源汽车同时随机停入试点区域(停车前所有车位都空置),请问2辆新能源汽车能同时充上电的概率为( )
[对点训练3](1)(2021·全国甲,理10)将4个1和2个0随机排成一行,则2个0不相邻的概率为( )
(2)(2024·山东青岛模拟)将四位数2 024的各个数字打乱顺序重新排列,则所组成的不同的四位数(含原来的四位数)中两个2不相邻的概率为( )
解析 将2 024各个数字打乱顺序重新排列所组成的不同四位数(含原来的四位数)的样本点有2 204,2 240,4 220,4 022,2 024,2 420,2 042,2 402,4 202,共9个,其中两个2不相邻的样本点有2 024,2 420,2 042,2 402,4 202,共5个,
考点四 古典概型与统计的综合应用
例5(2024·陕西铜川模拟)为进一步巩固提升全国文明城市,加速推行垃圾分类制度,某市推出了两套方案,并分别在A,B两个大型居民小区内试行.方案一:进行广泛的宣传活动,向小区居民和社会各界宣传垃圾分类的意义,讲解分类垃圾桶的使用方式,垃圾投放时间等,定期召开垃圾分类会议和知识宣传教育活动;方案二:在小区内设立智能化分类垃圾桶,智能垃圾桶操作简单,居民可以通过手机进行自动登录、称重、积分等一系列操作,并建立激励机制,比如,垃圾分类换积分兑换礼品等,以激发带动居民参与垃圾分类的热情.经过一段时间试行之后,在这两个小区内各随机抽取了100名居民进行问卷调查,记录他们对试行方案的满意度得分(满分100分),将数据分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并整理得到如下频率分布直方图:
(1)请通过频率分布直方图分别估计两种方案满意度的平均得分,判断哪种方案的垃圾分类推广措施更受居民欢迎(同一组中的数据用该组中间的中点值作代表);(2)以样本频率估计概率,若满意度得分不低于70分认为居民赞成推行此方案,低于70分认为居民不赞成推行此方案,规定小区居民赞成率不低于70%才可在该小区继续推行该方案,判断两小区哪个小区可继续推行方案?(3)根据(2)中结果,从可继续推行方案的小区所抽取100人中再按居民态度是否赞成,用分层随机抽样的方法抽取8人样本作为代表团,从代表团中选取两人做汇总发言,求至少有一个不赞成的居民被选到发言的概率.
(2)由题意可知:方案一中,满意度得分不低于70的频率为(0.031+0.021+0.010)×10=0.62,以频率估计概率,赞成率为62%<70%;B小区即方案二中,满意度不低于70分的频率为(0.020+0.032+0.023)×10=0.75,以频率估计概率,赞成率为75%>70%.∴B小区可继续推行方案二.
(3)由(2)中结果,在B小区不赞成25人中抽取8×25%=2人,赞成的75人中取8×75%=6人,组成代表团,设至少有一个不赞成居民做汇总发言的概率为P.记不赞成的两人为a,b,赞成的6人为1,2,3,4,5,6,从中任选两人,则有以下情况:ab,a1,a2,a3,a4,a5,a6,b1,b2,b3,b4,b5,b6,12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共28种,其中至少有一个不赞成的居民被选到发言的有
[对点训练4]为了解某班学生喜爱运动是否与性别有关,对全班进行问卷调查得到如下2×2列联表.
(1)若a=10,依据α=0.05的独立性检验,能否认为喜爱运动与性别有关?
解 (1)零假设为H0:喜爱运动与性别无关.当a=10时,2×2列联表如下:
2024版新教材高考数学全程一轮总复习第十章计数原理概率随机变量及其分布第三节随机事件的概率与古典概型课件: 这是一份2024版新教材高考数学全程一轮总复习第十章计数原理概率随机变量及其分布第三节随机事件的概率与古典概型课件,共54页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,基本结果,稳定于,事件的关系与运算,A⊆B,A∪B,A∩B,PA+PB,-PA等内容,欢迎下载使用。
2024版高考数学一轮总复习第10章计数原理概率随机变量及其分布第4节古典概型与事件的相互独立性课件: 这是一份2024版高考数学一轮总复习第10章计数原理概率随机变量及其分布第4节古典概型与事件的相互独立性课件,共47页。PPT课件主要包含了PAPB等内容,欢迎下载使用。
适用于新教材2024版高考数学一轮总复习第十一章计数原理概率随机变量及其分布第四节随机事件的概率与古典概型课件北师大版: 这是一份适用于新教材2024版高考数学一轮总复习第十一章计数原理概率随机变量及其分布第四节随机事件的概率与古典概型课件北师大版,共44页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,事件的分类,3由所给数据得,答案D等内容,欢迎下载使用。












