适用于新高考新教材备战2025届高考数学一轮总复习课时规范练81离散型随机变量及其分布列数字特征新人教A版

展开

这是一份适用于新高考新教材备战2025届高考数学一轮总复习课时规范练81离散型随机变量及其分布列数字特征新人教A版，共7页。

A.10B.15C.40D.45
2.设0则当a在(0,1)内增大时( )
A.D(X)增大B.D(X)减小
C.D(X)先减小后增大D.D(X)先增大后减小
3.(多选题)已知投资A,B两种项目获得的收益分别为X,Y,分布列如下表,则( )

A.m+n=0.5
B.E(2X+1)=4
C.投资两种项目的收益期望一样多
D.投资A项目的风险比B项目高
4.一个不透明的盒子中有质地、大小相同的5个球,其中红球3个,黄球2个,每次不放回地随机从盒子中取1个球,当盒子中只剩一种颜色时,停止取球.
(1)求盒子中恰好剩2个红球的概率;
(2)停止取球时,记盒子中所剩球的个数为X,求X的分布列与均值.
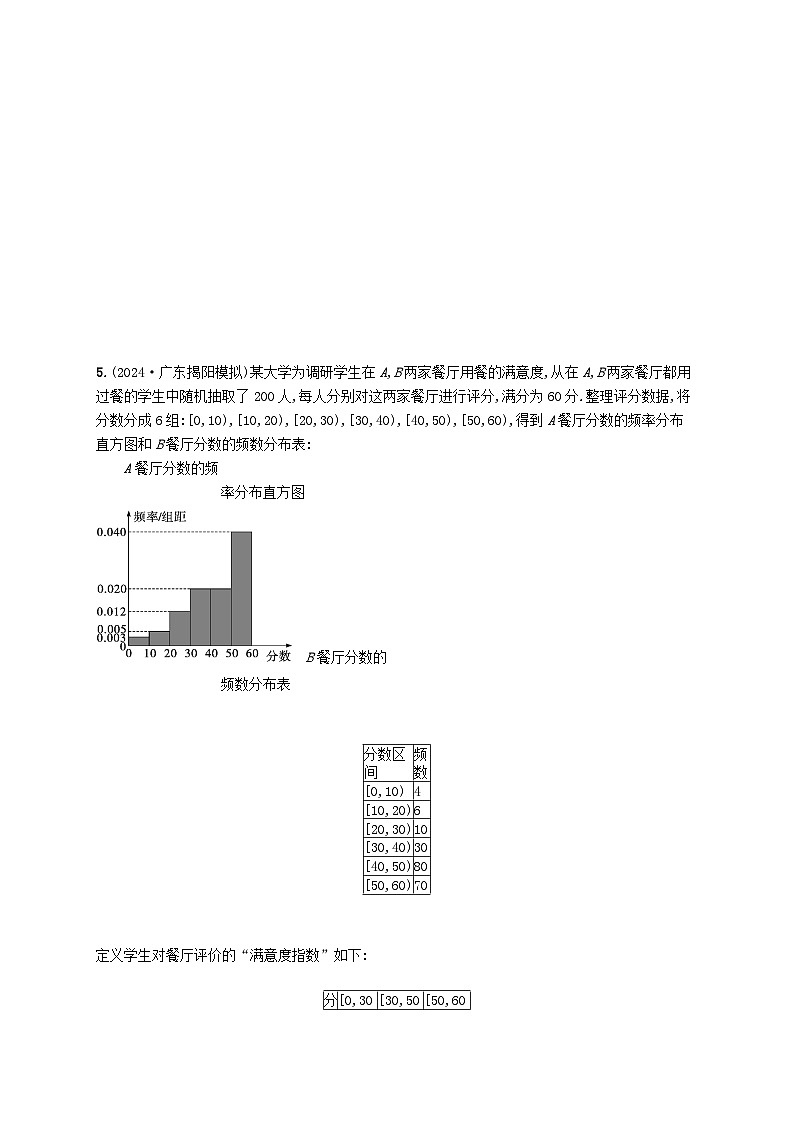
5.(2024·广东揭阳模拟)某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了200人,每人分别对这两家餐厅进行评分,满分为60分.整理评分数据,将分数分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60),得到A餐厅分数的频率分布直方图和B餐厅分数的频数分布表:
A餐厅分数的频
率分布直方图
B餐厅分数的
频数分布表
定义学生对餐厅评价的“满意度指数”如下:
(1)在随机抽取的200人中,求对A餐厅评价的“满意度指数”为4的人数;
(2)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”低的概率;
(3)如果根据学生对餐厅评价的“满意度指数”从A,B两家餐厅中选择一家用餐,从期望的角度你会选择哪一家?并说明理由.
6.(2024·山西太原模拟)对某地区过去20年的年降水量(单位:毫米)进行统计,得到以下数据:
887 939 643 996 715 838 1 082 923 901
1 182 1 035 863 772 943 1 035 1 022 855
1 118 768 809
将年降水量处于799毫米及以下、800至999毫米、1 000毫米及以上分别指定为降水量偏少、适中、偏多三个等级.
(1)将年降水量处于各等级的频率作为概率,分别计算该地区年降水量偏少、适中、偏多的概率;
(2)根据经验,种植甲、乙、丙三种农作物在年降水量偏少、适中、偏多的情况下可产出的年利润(单位:千元/亩)如下表所示.你认为这三种作物中,哪一种最适合在该地区推广种植?请说明理由.
7.(2024·湖南雅礼中学模拟)2024年中非经贸合作座谈会议在长沙举行,拟在某单位招募5名志愿者,该单位甲、乙、丙三个部门可分别向单位推选3名志愿者以供选拔,每个部门有3个小组,每个小组可向本部门推选2名志愿者供部门选拔,假设每名志愿者入选的机会相等.
(1)求甲部门志愿者入选人数为1人的概率;
(2)求所招募的5名志愿者来自三个部门的概率;
(3)求某小组志愿者入选人数X的分布列及期望.
课时规范练81 离散型随机变量及其分布列、数字特征
1.D 解析由题意得+m+=1,得m=,所以E(Y)=0+2a=3,解得a=6,所以D(Y)=(0-3)2+(2-3)2+(6-3)2=5,所以D(3Y-5)=32D(Y)=9×5=45.
2.A 解析根据随机变量分布列的性质可知+b=1,所以b=a,所以E(X)=0+1+2b=(1+2a),所以D(X)=[0-(1+2a)]2+[1-(1+2a)]2+[2-(1+2a)]2=-a2+a+=-(a-1)2+,又03.ACD 解析依题意可得0.2+m+0.6=1,所以m=0.2,0.3+0.4+n=1,所以n=0.3,所以m+n=0.5,故A正确;
所以E(X)=-1×0.2+0×0.2+2×0.6=1,则E(2X+1)=2E(X)+1=3,故B错误;
E(Y)=0×0.3+1×0.4+2×0.3=1,所以E(X)=E(Y),故C正确;
因为D(X)=(-1-1)2×0.2+(0-1)2×0.2+(2-1)2×0.6=1.6,D(Y)=(0-1)2×0.3+(1-1)2×0.4+(2-1)2×0.3=0.6,即D(X)>D(Y),所以投资A项目的风险比B项目高,故D正确.故选ACD.
4.解 (1)因为恰好剩2个红球,所以第1次和第2次必是1个红球和1个黄球,第3次必是黄球,所以盒子中恰好剩2个红球的概率P=
(2)X的所有可能取值为1,2,3,
P(X=1)=,
P(X=2)=,
P(X=3)=,
所以X的分布列为
E(X)=1+2+3
5.解 (1)由对A餐厅分数的频率分布直方图,得对A餐厅评价的“满意度指数”为4的频率为(0.020+0.020)×10=0.4,所以,对A餐厅评价的“满意度指数”为4的人数为200×0.4=80(人).
(2)设“对A餐厅评价的‘满意度指数’比对B餐厅评价的‘满意度指数’低”为事件C.
记“对A餐厅评价的‘满意度指数’为3”为事件A1;“对A餐厅评价的‘满意度指数’为4”为事件A2;
“对B餐厅评价的‘满意度指数’为4”为事件B1;“对B餐厅评价的‘满意度指数’为5”为事件B2.
所以P(A1)=(0.003+0.005+0.012)×10=0.2,P(A2)=(0.020+0.020)×10=0.4,
由频率估计概率得P(B1)==0.55,P(B2)==0.35.所以P(C)=P(A1B1+A1B2+A2B2)=P(A1)·P(B1)+P(A1)P(B2)+P(A2)·P(B2)=0.2×0.55+0.2×0.35+0.4×0.35=0.32,
所以该学生对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”低的概率为0.32.
(3)设对A餐厅评价的“满意度指数”为X,对B餐厅评价的“满意度指数”为Y,则随机变量X的可能取值有3,4,5,P(X=3)=0.2,P(X=4)=0.4,P(X=5)=0.4,所以对A餐厅评价的“满意度指数”X的分布列为
所以E(X)=3×0.2+4×0.4+5×0.4=4.2.
随机变量Y的可能取值有3,4,5,P(Y=3)=0.1,P(Y=4)=0.55,P(Y=5)=0.35,所以B餐厅评价的“满意度指数”Y的分布列为
所以E(Y)=3×0.1+4×0.55+5×0.35=4.25.
因为E(X)6.解 (1)将过去20年的年降水量按照降水量等级分类,可知:
降水量偏少有4年,概率可估计为=0.2;
降水量适中有10年,概率可估计为=0.5;
降水量偏多有6年,概率可估计为=0.3.
于是该地区年降水量偏少、适中、偏多的概率分别为0.2,0.5,0.3.
(2)设种植农作物甲、乙、丙一年后每亩地获得利润分别是随机变量X,Y,Z,
X的分布列为
故种植甲则每亩地获利的期望E(X)=8×0.5+12×0.5=10,
Y的分布列为
故种植乙则每亩地获利的期望E(Y)=12×0.2+10×0.5+7×0.3=9.5,
Z的分布列为
故种植丙则每亩地获利的期望E(Z)=7×0.2+10×0.5+12×0.3=10,
所以E(Y)D(Z)=0.2×(7-10)2+0.5×(10-10)2+0.3×(12-10)2=3,
D(X)>D(Z),故种植丙时获利的稳定性更好,因此,农作物丙最适合在该地区推广种植.
7.解 (1)由题意,甲部门志愿者入选人数为1人的概率为
(2)由题意,所招募的5名志愿者来自三个部门的概率为1-
(3)由题意可知X的可能取值为0,1,2,
P(X=1)=,P(X=2)=,
P(X=0)=1-P(X=1)-P(X=2)=,所以X的分布列为
所以E(X)=0+1+2Y
0
2
a
P
m
X
0
1
2
P
b
X
-1
0
2
P
0.2
m
0.6
Y
0
1
2
P
0.3
0.4
n
分数区间
频数
[0,10)
4
[10,20)
6
[20,30)
10
[30,40)
30
[40,50)
80
[50,60)
70
分数
[0,30)
[30,50)
[50,60)
满意度指数
3
4
5
年降水量
偏少
适中
偏多
甲
8
12
8
乙
12
10
7
丙
7
10
12
X
1
2
3
P
X
3
4
5
P
0.2
0.4
0.4
Y
3
4
5
P
0.1
0.55
0.35
X
8
12
P
0.5
0.5
Y
12
10
7
P
0.2
0.5
0.3
Z
7
10
12
P
0.2
0.5
0.3
X
0
1
2
P