

备战2025届新高考数学一轮总复习课时规范练50球与几何体的切接问题(附解析人教A版)
展开1.(2020·天津,5)若棱长为2的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12πB.24πC.36πD.144π
2.(2024·贵州凯里一中模拟)已知某封闭的直三棱柱各棱长均为2,若三棱柱内有一个球,则该球表面积的最大值为( )
A.B.C.4πD.
3.(2024·浙江余姚模拟)在正四棱锥S-ABCD中,底面是边长为2的正方形,侧面是腰长为的等腰三角形,则正四棱锥S-ABCD的外接球的体积为( )
A.B.9πC.D.18π
4.(2024·江西南昌模拟)在三棱锥P-ABC中,已知PA=BC=2,AC=PB=,PC=AB=,则三棱锥P-ABC外接球的表面积为( )
A.77πB.64πC.108πD.72π
5.(2021·天津,6)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1∶3,则这两个圆锥的体积之和为( )
A.3πB.4πC.9πD.12π
6.(2024·广东深圳模拟)已知正三棱锥的外接球半径R为1,则该正三棱锥的体积的最大值为( )
A.B.C.D.
7.(多选题)(2024·辽宁辽阳模拟)正三棱锥P-ABC的底面边长为3,高为,则下列结论正确的是( )
A.AB⊥PC
B.三棱锥P-ABC的表面积为9
C.三棱锥P-ABC的外接球的表面积为27π
D.三棱锥P-ABC的内切球的表面积为
8.将一个直角边长为2的等腰直角三角形绕其直角边所在的直线旋转一周所得圆锥的内切球的表面积为 .
9.(2024·陕西汉中模拟)在如图所示的直三棱柱ABC-A1B1C1中,△ABC是直角三角形,AA1=AC=5,AB=3,BC=4,则堑堵ABC-A1B1C1的外接球的体积是 .
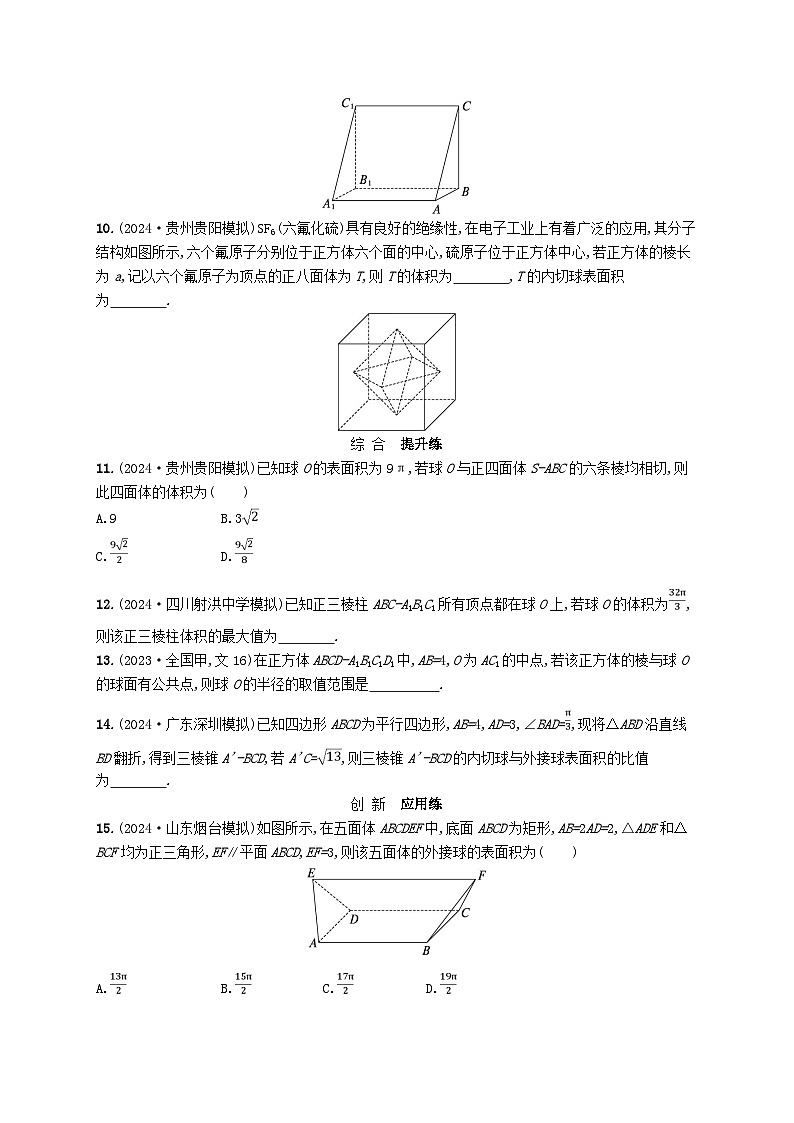
10.(2024·贵州贵阳模拟)SF6(六氟化硫)具有良好的绝缘性,在电子工业上有着广泛的应用,其分子结构如图所示,六个氟原子分别位于正方体六个面的中心,硫原子位于正方体中心,若正方体的棱长为a,记以六个氟原子为顶点的正八面体为T,则T的体积为 ,T的内切球表面积为 .
综 合 提升练
11.(2024·贵州贵阳模拟)已知球O的表面积为9π,若球O与正四面体S-ABC的六条棱均相切,则此四面体的体积为( )
A.9B.3
C.D.
12.(2024·四川射洪中学模拟)已知正三棱柱ABC-A1B1C1所有顶点都在球O上,若球O的体积为,则该正三棱柱体积的最大值为 .
13.(2023·全国甲,文16)在正方体ABCD-A1B1C1D1中,AB=4,O为AC1的中点,若该正方体的棱与球O的球面有公共点,则球O的半径的取值范围是 .
14.(2024·广东深圳模拟)已知四边形ABCD为平行四边形,AB=4,AD=3,∠BAD=,现将△ABD沿直线BD翻折,得到三棱锥A'-BCD,若A'C=,则三棱锥A'-BCD的内切球与外接球表面积的比值为 .
创 新 应用练
15.(2024·山东烟台模拟)如图所示,在五面体ABCDEF中,底面ABCD为矩形,AB=2AD=2,△ADE和△BCF均为正三角形,EF∥平面ABCD,EF=3,则该五面体的外接球的表面积为( )
A.B.C.D.
课时规范练50 球与几何体的切、接问题
1.C 解析 这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即R==3,所以这个球的表面积为S=4πR2=4π×32=36π.
2.A 解析 设底面三角形的内切圆的半径为r,则(2+2+2)·r=2×2sin,解得r=,小于高的一半1,所以该球的最大半径为,所以球的表面积的最大值为4πr2=
3. C 解析 如图所示,不妨设该四棱锥外接球的球心O在线段SE上,球心O在线段SE的延长线的情况可同理讨论.设球的半径为R.三棱锥的底面中心为E,连接SE,BO,BE.因为在正四棱锥S-ABCD中,底面是边长为2的正方形,侧面是腰长为的等腰三角形,所以BE=,SE==2.在Rt△OBE中,OB2=OE2+BE2,即R2=(2-R)2+()2,解得R=球心O在线段SE的延长线上时,可得R2=(R-2)2+()2,解得R=所以外接球的体积为V=R3=
4.A 解析 因为三棱锥的对棱相等,所以可以把它补成一个长方体.设长方体的同一顶点的三条棱长分别为a,b,c,且长方体的面对角线长为2,则=2,此长方体体对角线为长方体外接球直径,即为该三棱锥外接球的直径,设此外接球半径为R,则2R=,R=,所以球的表面积为4πR2=77π.
5.B 解析 如图所示,设两个圆锥的底面圆圆心为点D,设圆锥AD和圆锥BD的高之比为3∶1,即AD=3BD.
设球的半径为R,则,可得R=2,所以AB=AD+BD=4BD=4,所以BD=1,AD=3.因为CD⊥AB,AC⊥BC,所以∠CAD+∠ACD=∠BCD+∠ACD=90°,所以∠CAD=∠BCD,又因为∠ADC=∠BDC,所以△ACD∽△CBD,所以,所以CD=因此,这两个圆锥的体积之和为CD2·(AD+BD)=3×4=4π.
6. C 解析 如图所示,设该正三棱锥的高为h,底面外接圆的圆心是点O1,半径为r,底面面积为S,球心是点O.当球心O在线段SO1上时,由球的截面圆的性质,可得OA2=A+O,即R2=r2+(h-R)2,同理,当球心O在线段SO1的延长线上时,可得R2=r2+(R-h)2,解得R==1,即r2=2h-h2>0,解得0
7. ABD 解析 如图,取棱AB的中点D,连接CD,PD.则在正三棱锥P-ABC中,AB⊥CD,AB⊥PD.因为PD,CD⊂平面PCD,且PD∩CD=D,所以AB⊥平面PCD,则AB⊥PC,故A正确;作PH⊥平面ABC,垂足为H,则PH=由正三棱锥的性质可知H在CD上,且CH=2DH.因为AB=3,所以CD=,则CH=因为PH=,所以PC==3,则三棱锥P-ABC的表面积S=9×4=9,故B正确;设三棱锥P-ABC的外接球的球心为O,半径为R,则O在PH上,连接OC,则R2=CH2+OH2=(PH-OH)2,即R2=3+OH2=(-OH)2,解得R2=,则三棱锥P-ABC的外接球的表面积为4πR2=,故C错误;设三棱锥P-ABC的内切球的半径为r,则VP-ABC=99r,解得r=,从而三棱锥P-ABC的内切球的表面积为4πr2=,故D正确.故选ABD.
8.(48-32)π 解析 依题意,作圆锥的轴截面为等腰直角三角形,
截得其内切球的大圆是此等腰直角三角形的内切圆,圆锥的底面半径为2,则其母线长为2,设圆锥的内切球半径为r,则2r+2r+4×r=4×2,所以r=2(-1),所以内切球的表面积为4πr2=16(3-2)π=(48-32)π.
9 解析 将该直三棱柱补为一个长方体,
如图,则该直三棱柱的外接球即为长方体的外接球,设长方体的体对角线长为d,则d2=32+42+52=50,所以d=5,所以外接球的体积为()3=
10 解析 正八面体T可视为两个全等的正四棱锥拼接而成,且该正四棱锥的底面边长为,高为,所以正八面体的体积为V=2()2由题图可知,正八面体T的每个面都是棱长为的等边三角形,所以正八面体T的表面积为S=8()2=a2.设正八面体T的内切球半径为r,则V=Sr,所以r=,因此正八面体T的内切球的表面积为4πr2=4π×()2=
11.A 解析 设球O的半径是R,由4πR2=9π,∴R=将正四面体放到正方体中,正方体的内切球即与正四面体的六条棱均相切.∵R=,∴正方体的棱长为3,则正四面体棱长为3,底面ABC上的高h==2,∴V=S△ABCh=(3)2×2=9.
12. 8 解析 设正三棱柱ABC-A1B1C1的上、下底面的中心分别为O1,O2,连接O1O2,根据对称性可得,线段O1O2的中点O即为正三棱柱ABC-A1B1C1的外接球的球心,线段OA为该外接球的半径,设OA=R.由已知R3=,所以R=2,即OA=2.设正三棱柱ABC-A1B1C1的底面边长为x,设线段BC的中点为D,则AD=x,AO1=AD=由<2,知x<2,所以0
第三步,由图可知棱切球半径r1=AD1=4=2,外接球半径r2=BD1=4=2,球O半径的取值范围是[2,2].
(方法二)由对称性知,只需考虑球与正方体的棱有公共点,正方体中心O到一条棱的最短距离即为到棱中点的距离,为2,到一条棱的最长距离即为到棱顶点的距离,为2,故r∈[2,2].
14 解析 在△ABD中,AB=4,AD=3,∠BAD=,故DB2=AB2+AD2-2AB·AD·cs∠BAD=42+32-2×4×3=13,即DB=
则在三棱锥A'-BCD中,A'C=DB,A'B=AB=DC,A'D=AD=BC,即此三棱锥的对棱相等,故此三棱锥的三组对棱是一个长方体的六个面的对角线,设该长方体从同一个顶点出发的三条棱长分别为a,b,c,则解得此长方体的外接球是三棱锥A'-BCD的外接球,设外接球的半径为R1,则2R1=,即R1=三棱锥A'-BCD的体积V=abc-4abc=abc=2,因为三棱锥A'-BCD的四个面是全等的三角形,所以三棱锥A'-BCD的表面积是S=4S△ABD=4AB·AD·sin=2×4×3=12
设内切球半径为R2,以内切球球心为顶点,把三棱锥分割为以球心为顶点,四个面为底面的四个小三棱锥,四个小三棱锥体积之和等于大三棱锥的体积,故R2=,则三棱锥A'-BCD的内切球与外接球表面积的比值为
15.D 解析 连接AC,BD交于点M,取EF的中点O,因为四边形ABCD是矩形,且EA=ED=FB=FC,EF∥平面ABCD,EF>AB,所以点O在平面ABCD的射影为点M.连接OM,则OM⊥平面ABCD.取BC的中点G,连接FG,作GH⊥EF,垂足为H,如图所示.
由题可知HF=,FG=,在Rt△FHG中,HG=,所以OM=HG=因为底面ABCD为矩形,OM⊥平面ABCD,所以外接球球心在直线OM上,且到多边形各顶点的距离相等.若球心O'在线段MO上,设O'M=x,则O'O=-x,x2+AM2=(-x)2+OE2,即x2+=(-x)2+,解得x=(舍).若球心O'在线段MO的延长线上,设OO'=y,外接球的半径为R,连接O'E,O'A,显然O'E=O'A=R,则OE2+y2=R2且AM2+(OM+y)2=R2,即解得y=,R2=所以外接球的表面积S=4πR2=4π
备战2025届新高考数学一轮总复习课时规范练69最值与范围问题(附解析人教A版): 这是一份备战2025届新高考数学一轮总复习课时规范练69最值与范围问题(附解析人教A版),共6页。试卷主要包含了已知椭圆C,如图,抛物线M,设点A,E,则B等内容,欢迎下载使用。
备战2025届新高考数学一轮总复习课时规范练70定点与定值问题(附解析人教A版): 这是一份备战2025届新高考数学一轮总复习课时规范练70定点与定值问题(附解析人教A版),共7页。试卷主要包含了已知椭圆E,已知双曲线C,已知抛物线C,求得HN的方程为y=,过点等内容,欢迎下载使用。
专题8.6 几何体与球切、接、截的问题(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题8.6 几何体与球切、接、截的问题(讲+练)-备战高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题86几何体与球切接截的问题原卷版docx、专题86几何体与球切接截的问题解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。












