第18章 平行四边形小结（第2课时）人教版数学八年级下册上课课件

这是一份第18章 平行四边形小结（第2课时）人教版数学八年级下册上课课件，共33页。
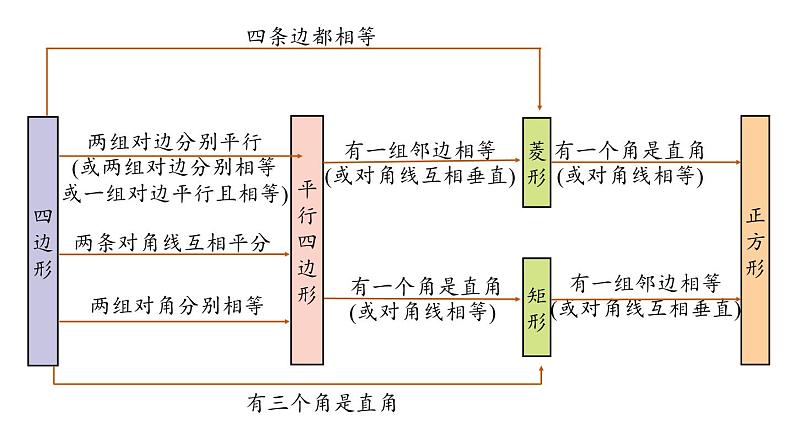
18 平行四边形 小结八年级下册 RJ初中数学课时2一、矩形1.定义和性质定义： 有一个角是直角的平行四边形叫做矩形.特殊性质： ①四个角都是直角；②对角线相等；③轴对称图形.直角三角形斜边上中线的性质：直角三角形斜边上的中线等于斜边的一半.知识梳理2.判定判定1（定义法）： 有一个角是直角的平行四边形是矩形.判定2： 有三个角是直角的四边形是矩形.判定3： 对角线相等的平行四边形是矩形.二、菱形1.定义、性质、面积定义： 有一组邻边相等的平行四边形是菱形.特殊性质： ①四条边都相等；②对角线互相垂直，并且每一条对角线平分一组对角；③轴对称图形.面积： ①菱形的面积=底×高； ②菱形的面积=对角线长的乘积的一半.2.判定判定1（定义法）： 有一组邻边相等的平行四边形是菱形.判定2 ： 四条边相等的四边形是菱形.判定3 ： 对角线互相垂直的平行四边形是菱形.三、正方形1.定义和性质定义： 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.特殊性质： ①对边平行，四边相等；②四个角都是直角；③两条对角线互相垂直平分且相等，每条对角线平分一组对角；④轴对称图形.判定1：对角线互相垂直的矩形是正方形.判定2：有一组邻边相等的矩形是正方形.判定3：对角线相等的菱形是正方形.判定4：有一个角是直角的菱形是正方形.2.判定四边形平行四边形正方形菱形矩形四条边都相等两组对边分别平行(或两组对边分别相等或一组对边平行且相等)两条对角线互相平分有一组邻边相等(或对角线互相垂直)有一个角是直角(或对角线相等)两组对角分别相等有一个角是直角(或对角线相等)有一组邻边相等(或对角线互相垂直)有三个角是直角1.如果矩形ABCD的对角线AC=10，一边AB=6，则它的另一边BC及周长是多少？解：∵四边形ABCD是矩形,∴∠B=90〫. 四边形ABCD的周长=AB+BC+CD+DA=6+8+6+8=28.重难点1：矩形的性质及判定重点解析2.已知矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点，且AE=BF=CG=DH，求证：四边形EFGH为矩形.证明：∵四边形ABCD是矩形,∴ AO=BO=CO=DO.∵ AE=BF=CG=DH，OE=OA-AE， OF=OB-BF， OG=OC-CG， OH=OD-DH,∴ OE=OF=OG=OH,∴四边形EFGH是矩形.  D重难点2：菱形的性质及判定重点解析 ∵AC+BD=6，∴ AO+BO=3,   2.如图，在三角形ABC中，AB=AC，点D,E,F分别是三角形ABC三边的中点. 求证：四边形ADEF是菱形.证明：∵点D,E,F分别是三角形ABC三边的中点, ∴四边形ADEF是平行四边形.∵AB=AC , ∴四边形ADEF是菱形.∴ DE=EF,1.如图，在正方形ABCD中，点E,F分别在BC,CD上，BE=CF，则图中与∠AEB相等的角的个数是（ ）.A. 1个 B. 2个 C. 3个 D. 4个 C△ABE≌△BCF， AD//BC，AB//CD∠AEB=∠BFC=∠DAE= ∠ABF重难点3：正方形的性质及判定重点解析2.如图，四边形ABCD为平行四边形，再从①AB=BC，②∠ABC=90〫，③AC=BD， ④AC⊥BD四个条件中，选择两个作为补充条件，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（ ）.BA.①② B.②③C.①③ D.②④1.如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，且AF=BD，连接BF.（1）线段BD与CD有什么数量关系，并说明理由；（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由.深化练习解：（1）BD=CD.∵AF//CB,∴∠AFE=∠DCE. ∵ E是AD的中点,∴AE=DE. ∵在△AEF和△DEC中 ，∠AFE=∠DCE，∠AEF=∠DEC ， AE=DE,∴△AEF≌△DEC（AAS）,∴AF=CD.∵AF=BD,∴BD=CD.（2）当△ABC满足AB=AC时，四边形AFBD是矩形.∵AF//BD，AF=BD,∴四边形AFBD是平行四边形.∵AB=AC，BD=CD,∴∠ADB=90〫,∴四边形AFBD是矩形.2.如图，已知菱形ABCD，AB=AC，E，F分别是边BC，AD的中点，连接AE，CF.求证：四边形AECF是矩形.证明：∵四边形ABCD是菱形，∴AD//BC，AD=BC，AB=BC.∵AB=AC ，∴△ABC是等边三角形.∵E，F分别是边BC，AD的中点, ∴AF//EC， AF=EC,∴四边形AECF是平行四边形.∵∠AEC=90〫,∴四边形AECF是矩形. 3.如图，在菱形纸片 ABCD 中，∠A=60〫，折叠菱形纸片ABCD，使点 C 落在 DP（P 为 AB 的中点）所在的直线上，得到经过点 D 的折痕 DE，则 ∠DEC 的度数为（ ）.78〫 B. 75〫 C. 60〫 D. 45〫B解析：如图，连接BD.∵四边形ABCD是菱形，∴AD=AB.∵∠A=60〫，∴△DAB为等边三角形. ∵点P为AB的中点，∴DP⊥AB.∵DC//AB ，∴∠PDC=∠DPA=90〫.∵△DEC' 是△DEC沿DE折叠得到的, 在△DEC中，∠DEC=180〫-∠CDE-∠C=75〫.4.如图，在平行四边形ABCD中，BE 平分∠ABC 交 AD 于点 E，DF 平分∠ADC 交 BC 于点 F.（1）求证：△ABE≌△CDF；（2）若BD⊥EF ，求证：四边形EBFD是菱形.（1）证明： ∵四边形ABCD是平行四边形,∴∠A=∠C，AB=CD，∠ABC=∠ADC.∵ BE平分∠ABC，DF平分∠ADC,∴∠ABE=∠CDF.∵∠A=∠C， AB=CD ，∠ABE=∠CDF,∴△ABE≌△CDF（ASA）.（2）证明： ∵△ABE≌△CDF,∴AE=CF.∵四边形ABCD是平行四边形,∴AD//BC， AD=BC,∴ DE//BF，DE=BF,∴四边形EBFD是平行四边形.∵ BD⊥EF,∴四边形EBFD是菱形.5.在矩形ABCD中， AD=2CD，E是AD的中点，BF//CE，CF//BE. 求证：四边形BECF是正方形. 证明： ∵ BF//CE，CF//BE,∴ 四边形BECF是平行四边形.∵在矩形ABCD中， AD=2CD，E是AD的中点,∴ AE=AB=DE=DC.∵在△ABE和△DCE中 ，AB=DC， ∠A=∠D， AE=DE,∴△ABE≌△DCE（SAS）,∴BE=CE，∠AEB=∠DEC=45〫,∴∠BEC=90〫,∴四边形BECF是正方形.6.如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45〫， 则△EDF 的周长等于 .转化思想求周长：将△EDF 的周长转化为AD与CD的和.解：如图，延长FC至点G，使CG=AE，连接BG.∵四边形ABCD是正方形，∴AB=CB，∠A=∠ABC=∠BCD=90〫，∴∠A=∠BCG=90〫,∴△ABE≌△CBG（SAS）,∴∠ABE=∠CBG，BE=BG ，CG=AE.∵∠EBF=45〫,∴∠ABE+∠FBC =∠ABC-∠EBF=45〫G∴∠GBF=∠CBG +∠FBC =∠ABE+∠FBC=45〫∴∠GBF=∠EBF.∵在△BEF和△BGF中 ，BE=BG， ∠EBF=∠GBF， BF=BF,∴△BEF≌△BGF（SAS）,∴EF=FG=FC+CG=FC+AE,∴△DEF的周长为DE+DF+EF=DE+DF+AE+CF=AD+CD=4.技巧点拨：作辅助线构造全等三角形，实现边、角的转换在正方形中出现以正方形的一边为直角边的直角三角形时，经常通过延长或是旋转作辅助线构造全等三角形，从而实现边、角的转换.