江苏省南京市雨花台中学2023-2024学年七年级下学期3月月考数学试题(无答案)

这是一份江苏省南京市雨花台中学2023-2024学年七年级下学期3月月考数学试题(无答案)，共6页。试卷主要包含了非选择题部分请按题号用0，在草稿纸、试题卷上答题无效等内容，欢迎下载使用。
姓名：__________班级：________考场/座位号：______
注意事项
1.答题前，考生先将自己的姓名、班级、考场填写清楚，并认真核对条形码上的姓名和准考证号。
2.选择题部分请按题号用2B铅笔填涂方框，修改时用橡皮擦干净，不留痕迹。
3.非选择题部分请按题号用0.5毫米黑色墨水签字笔书写，否则作答无效。要求字体工整、笔迹清晰。作图时，必须用2B铅笔，并描浓。
4.在草稿纸、试题卷上答题无效。
5.请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁。
客观题
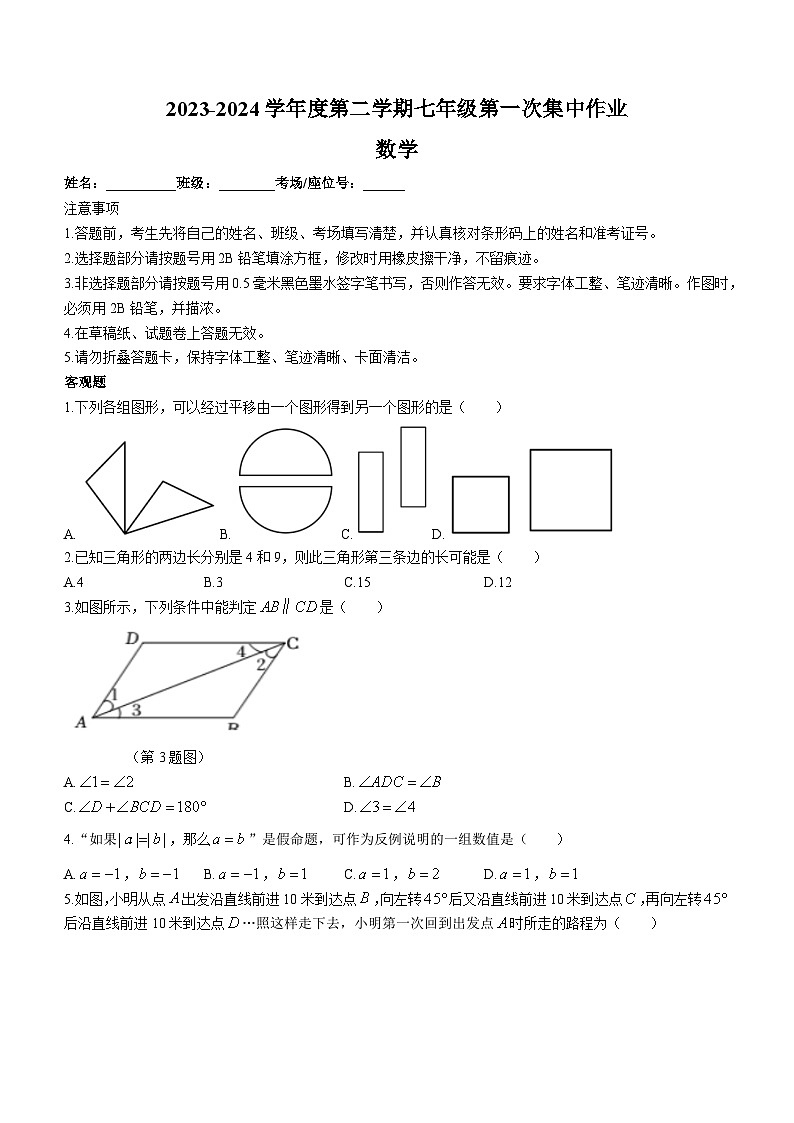
1.下列各组图形，可以经过平移由一个图形得到另一个图形的是（ ）
2.已知三角形的两边长分别是4和9，则此三角形第三条边的长可能是（ ）
A.4B.3C.15D.12
3.如图所示，下列条件中能判定是（ ）
（第3题图）
A.B.
C.D.
4.“如果，那么”是假命题，可作为反例说明的一组数值是（ ）
A.，B.，C.，D.，
5.如图，小明从点出发沿直线前进10米到达点，向左转后又沿直线前进10米到达点，再向左转后沿直线前进10米到达点…照这样走下去，小明第一次回到出发点时所走的路程为（ ）
（第5题图）
A.40米B.60米C.80米D.100米
6.如图，已知D、E分别为的边BC、AC的中点，连接AD、DE，AF为的中线.若四边形的面积为10，则的面积为（ ）
（第6题图）
A.12B.16C.18D.20
填空题
7.“两直线平行，内错角相等”的条件是：__________________；结论是_________________.
8.一个多边形的每个内角都为144°，那么该正多边形的边数为_________.
9.命题“同位角相等的逆命题是_________；逆命题是______命题（填“真”或“假”）.
10.直角三角形中两个锐角的差为20°，则较小的锐角度数是______°.
11.若等腰三角形两边的长分别为2、5，则这个三角形的周长为_______.
12.结合如图，用符号语言表达定理“同位角相等，两直线平行”的推理形式：
∵_______________，∴.
（第12题图）
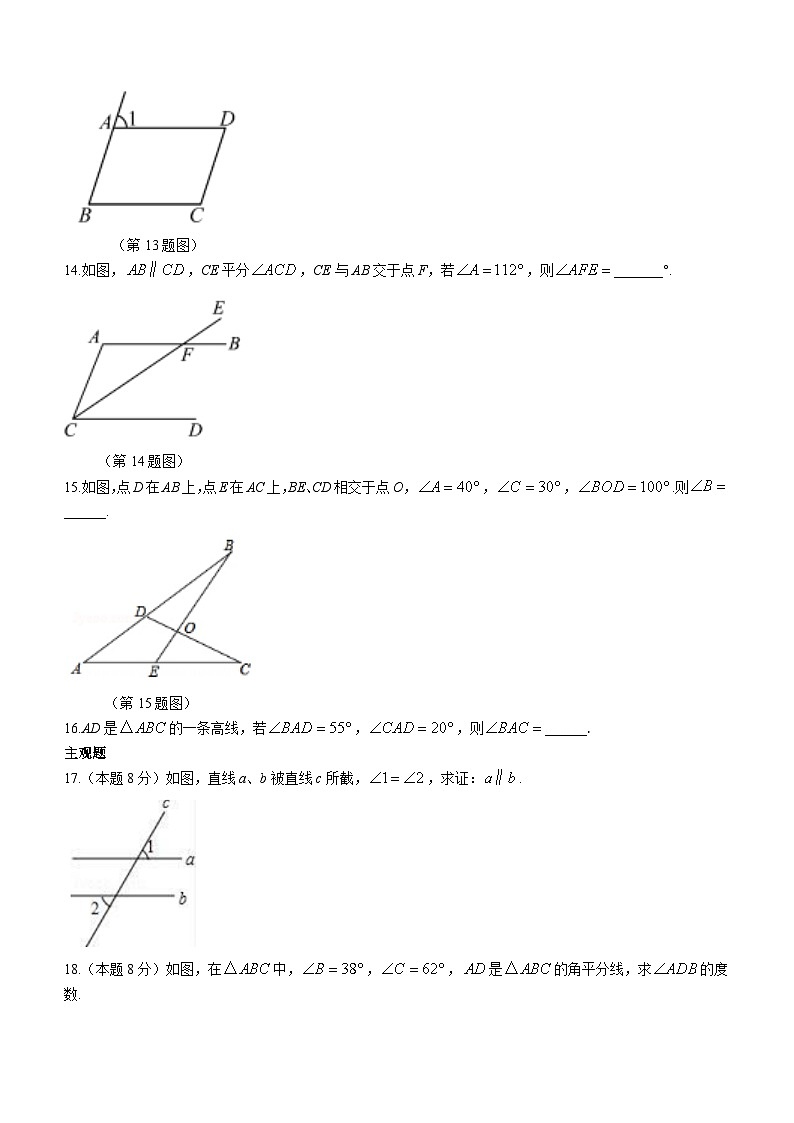
13.如图，在四边形中，，，是四边形的一个外角.若，则______°.
（第13题图）
14.如图，，CE平分，CE与AB交于点F，若，则_______°.
（第14题图）
15.如图，点D在AB上，点E在AC上，BE、CD相交于点O，，，.则______.
（第15题图）
16.AD是的一条高线，若，，则______.
主观题
17.（本题8分）如图，直线a、b被直线c所截，，求证：.
18.（本题8分）如图，在中，，，是的角平分线，求的度数.
19.（本题8分）在正方形网格中，每个小正方形的边长均为1个单位长度，的三个顶点的位置如图所示.现将沿着点A到点D的方向平移，使点A变换为点D，点E、F分别是B、C的对应点.
（I）画出中AC边上的高BH；
（2）请画出平移后的；
（3）平移后，线段AC扫过的部分所组成的封闭图形的面积是______.
20.（本题10分）证明：三角形内角和为180°.
已知：___________________________________.
求证：___________________________________.
证明：
21.（本题8分）已知：如图，直线AD与，分别相交于点，，与EC，BF分别相交于点，，，.求证：.
22.（本题8分）如图，在中，点在上，，，垂足分别为，，.求证：.
23.（本题8分）用两种方法证明“三角形的外角和等于”.
已知：如图，、、是的三个外角.
求证：.
证法1：_________________________，
.
__________________________________，
.
请把证法1补充完整，并用不同的方法完成证法2.
24.（本题10分）如图①，已知.点在上，点、在上.在中，，.点、在直线上，在中，，.
（1）的度数是______°；
（2）如图②，将沿直线AB平移，当点在上时，求的度数；
（3）将沿直线平移，当以、、为顶点的三角形中，有两个角相等时，请直接写出的度数.
（备用图）（备用图）