中考数学二轮复习考点培优专练专题六 几何最值问题（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点培优专练专题六 几何最值问题（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点培优专练专题六几何最值问题原卷版doc、中考数学二轮复习考点培优专练专题六几何最值问题解析版doc等2份试卷配套教学资源，其中试卷共76页， 欢迎下载使用。
例题（2022·全国·八年级）如图1，在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，AC＝8，点P为AC边上的一个动点，过点P作PD⊥AB于点D，求PB+PD的最小值．请在横线上补充其推理过程或理由．
练习题
1．（2020·山东·东营市实验中学三模）如图，正方形ABCD的边长为8，点M在DC上且DM＝2，N是AC上的一动点，则DN＋MN的最小值是______．
2．（2022·广西·上思县教育科学研究所八年级期末）如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是_____．
3．（2022·甘肃庆阳·八年级期末）如图，在等边△ABC中，E为AC边的中点，AD垂直平分BC，P是AD上的动点．若AD=6，则EP+CP的最小值为_______________．
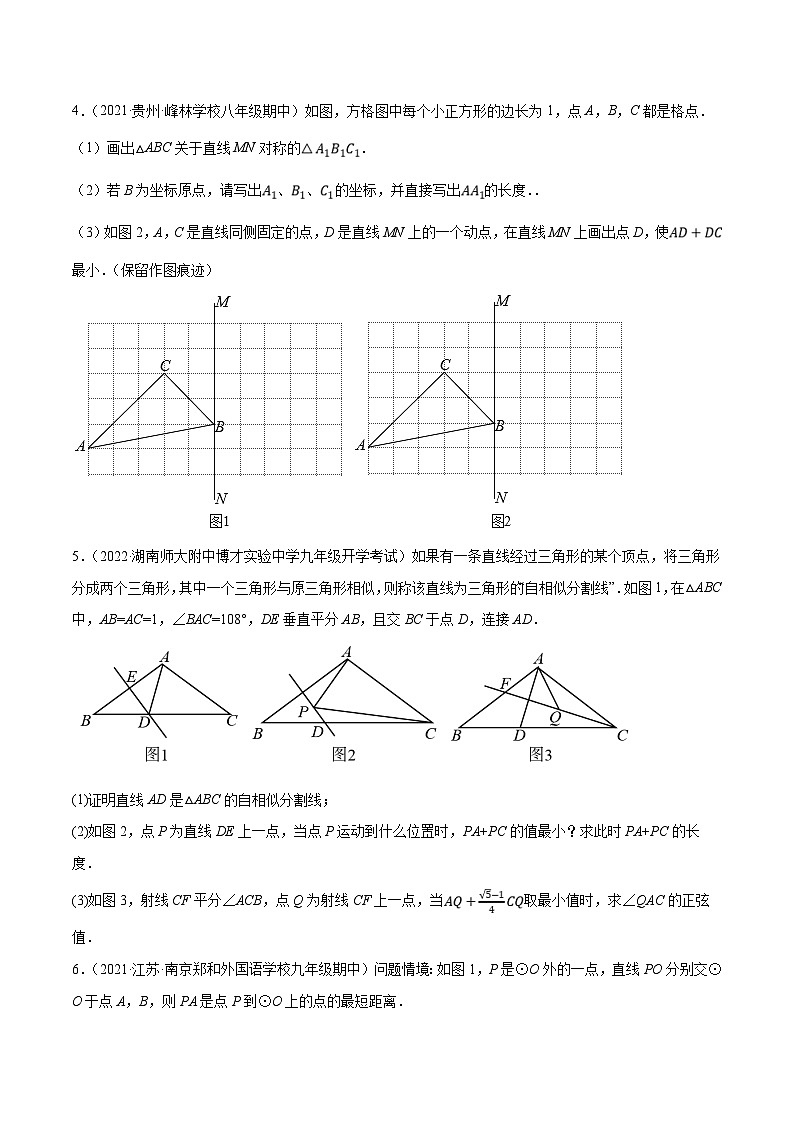
4．（2021·贵州·峰林学校八年级期中）如图，方格图中每个小正方形的边长为1，点A，B，C都是格点．
（1）画出△ABC关于直线MN对称的．
（2）若B为坐标原点，请写出、、的坐标，并直接写出的长度．．
（3）如图2，A，C是直线同侧固定的点，D是直线MN上的一个动点，在直线MN上画出点D，使最小．（保留作图痕迹）
5．（2022·湖南师大附中博才实验中学九年级开学考试）如果有一条直线经过三角形的某个顶点，将三角形分成两个三角形，其中一个三角形与原三角形相似，则称该直线为三角形的“自相似分割线”．如图1，在△ABC中，AB=AC=1，∠BAC=108°，DE垂直平分AB，且交BC于点D，连接AD．
(1)证明直线AD是△ABC的自相似分割线；
(2)如图2，点P为直线DE上一点，当点P运动到什么位置时，PA+PC的值最小？求此时PA+PC的长度．
(3)如图3，射线CF平分∠ACB，点Q为射线CF上一点，当取最小值时，求∠QAC的正弦值．
6．（2021·江苏·南京郑和外国语学校九年级期中）问题情境：如图1，P是⊙O外的一点，直线PO分别交⊙O于点A，B，则PA是点P到⊙O上的点的最短距离．
（1）探究证明：如图2，在⊙O上任取一点C（不与点A，B重合），连接PC，OC．求证：PA＜PC．
（2）直接应用：如图3，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是 ．
（3）构造运用：如图4，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A1MN，连接A1B，则A1B长度的最小值为 ．
（4）综合应用：如图5，平面直角坐标系中，分别以点A（﹣2，3），B（4，5）为圆心，以1，2为半径作⊙A，⊙B，M，N分别是⊙A，⊙B上的动点，P为x轴上的动点，直接写出PM+PN的最小值为 ．
二、线段最值问题
例题在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．
（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；
（2）如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；
（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．
练习题
1．（2021·广东·铁一中学九年级期中）如图，⊙M的半径为2，圆心M的坐标为（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为（ ）
A．3B．4C．5D．6
2．（2019·广西玉林·中考真题）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（ ）
A．5B．6C．7D．8
3．（2021·四川师范大学附属中学九年级阶段练习）如图，矩形ABCD中，AB＝2，BC＝3，点E，F分别在边AB，边BC上运动，点G在矩形内，且DG⊥CG，EF⊥FG，FG：EF＝1：2，则线段GF的最小值为_______．
4．（2021·全国·九年级专题练习）如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为______．
5．（2021·全国·九年级专题练习）在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，若线段MA绕点M旋转得线段MA′．
（1）如图①，线段MA'的长＝___．
（2）如图②，连接A'C，则A'C长度的最小值是___．
6．（2020·江苏扬州·中考真题）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点E为边AB上的一个动点，连接ED并延长至点F，使得 SKIPIF 1 < 0 ，以EC、EF为邻边构造 SKIPIF 1 < 0 ，连接EG，则EG的最小值为________．
三、周长、面积最值问题
例题（2021·云南昭通·八年级期中）如图，在 SKIPIF 1 < 0 中，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的垂直平分线交 SKIPIF 1 < 0 于点D，交 SKIPIF 1 < 0 于点E，连接 SKIPIF 1 < 0 ．
（1）若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的度数；
（2）若点P为直线 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 周长的最小值．
练习题
1．（2021·陕西·西安交通大学附属中学航天学校八年级阶段练习）如图，凸四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，若点M、N分别为边 SKIPIF 1 < 0 上的动点，则 SKIPIF 1 < 0 的周长最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．6D．3
2．（2021·河南省直辖县级单位·八年级期末）如图，在直角坐标系中，点A（2，2），C（4，4）是第一象限角平分线上的两点，点B的纵坐标为2，且BA＝CB，在y轴上取一点D，连接AB，BC，AD，CD，使得四边形ABCD的周长最小，则这个周长的最小值为____．
3．（2021·全国·九年级专题练习）如图，∠AOB＝45°，角内有一点P，PO＝10，在角两边上有两点Q、R（均不同于点O），则△PQR的周长最小值是____；当△PQR周长最小时，∠QPR的度数＝__．
4．（2021·湖北武汉·八年级期中）如图，将△ABC沿AD折叠使得顶点C恰好落在AB边上的点M处，D在BC上，点P在线段AD上移动，若AC＝6，CD＝3，BD＝7，则△PMB周长的最小值为 ___．
5．（2021·云南红河·八年级期末）在平面直角坐标系中，矩形纸片AOBC按如图方法放置，点A、B分别在y轴和x轴上，已知OA=2，OB=4，点D在边AC上，且AD=1．

解答下列问题．
（1）点C的坐标为 _______；
（2）在x轴上有一点E，使得△CDE的周长最短，求出点E的坐标及直线CE的解析式．
（3）在平面直角坐标系内是否存在点P，使得以C、D、P、E为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，说明理由．
6．（2021·山东·日照市田家炳实验中学一模）如图，已知抛物线y＝ax2+bx+c（a≠0）过原点O和点A(3，﹣3)，F(1， SKIPIF 1 < 0 )是该抛物线对称轴上的一个定点，过y轴上的点B(0， SKIPIF 1 < 0 )作y轴的垂线l．
（1）求抛物线的解析式；
（2）点P(m，n)是抛物线上的任意一点，过点P作直线l的垂线，垂足为M．求证：点P在线段FM的垂直平分线上；
（3）点E为线段OA的中点，在抛物线上是否存在点Q，使 SKIPIF 1 < 0 QEF周长最小？若存在，求点Q的坐标和 SKIPIF 1 < 0 QEF周长的最小值；若不存在，请说明理由．
7．（2021·重庆市万盛经济技术开发区溱州中学九年级阶段练习）已知如图，在 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上一点，连接 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 上一动点，连接 SKIPIF 1 < 0 ．
（1）如图1，当 SKIPIF 1 < 0 时，连接 SKIPIF 1 < 0 ，延长 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
（2）如图2，以 SKIPIF 1 < 0 为直角边作等腰 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，当点 SKIPIF 1 < 0 在运动过程中，求 SKIPIF 1 < 0 周长的最小值．
8．（2022·广东广州·八年级期末）在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2
(1)如图①，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；
(2)如图②，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；
(3)如图③，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．
9．（2021·湖北·沙市中学九年级阶段练习）如图，抛物线 SKIPIF 1 < 0 交x轴于 SKIPIF 1 < 0 两点，交y轴于点C SKIPIF 1 < 0 ，点Q为线段 SKIPIF 1 < 0 上的动点．
（1）求抛物线的解析式；
（2）求 SKIPIF 1 < 0 的最小值；
（3）过点Q作 SKIPIF 1 < 0 交抛物线的第四象限部分于点P，连接 SKIPIF 1 < 0 ，记 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，当S最大时，求点P的坐标，并求S的最大值．
四、隐形圆问题
例题（2021·全国·九年级专题练习）如图，在矩形ABCD中，AB＝6，AD＝8，点E，F分别是边CD，BC上的动点，且∠AFE＝90°
（1）证明：△ABF∽△FCE；
（2）当DE取何值时，∠AED最大．
练习题
1．（2021·山东济南·二模）如图，菱形ABCD的边AB=8，∠B=60°，BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点为A′．当CA′的长度最小时，CQ的长为（ ）
A．5B．7C．8D．6.5
2．（2021·全国·九年级课时练习）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 cm， SKIPIF 1 < 0 cm． SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上的一个动点，连接 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，在点 SKIPIF 1 < 0 变化的过程中，线段 SKIPIF 1 < 0 的最小值是（ ）
A．1B． SKIPIF 1 < 0 C．2D． SKIPIF 1 < 0
3．（2022·湖北荆州·九年级期末）如图，长方形ABCD中， SKIPIF 1 < 0 ，BC=2，点E是DC边上的动点，现将△BEC沿直线BE折叠，使点C落在点F处，则点D到点F的最短距离为________．
4．（2022·重庆·一模）如图，已知 SKIPIF 1 < 0 ，外心为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，分别以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为腰向形外作等腰直角三角形 SKIPIF 1 < 0 与 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值是______．
5．（2021·江苏泰州·九年级期中）如图，在Rt SKIPIF 1 < 0 ABC中，∠ACB＝90°，D为AC的中点，M为BD的中点，将线段AD绕A点任意旋转（旋转过程中始终保持点M为BD的中点），若AC＝8，BC＝6，那么在旋转过程中，线段CM长度的取值范围是____．
6．（2021·山东潍坊·九年级期中）如图，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的坐标分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为坐标平面内一动点，且 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 取最大值时，点 SKIPIF 1 < 0 的纵坐标为____．
7．（2021·全国·九年级课时练习）如图， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的直径， SKIPIF 1 < 0 ，点C为 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一动点，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点，求 SKIPIF 1 < 0 的最小值．
8．（2021·湖北·武汉第三寄宿中学九年级阶段练习）问题背景如图（1），△ABC为等腰直角三角形，∠BAC＝90°，直线l绕着点A顺时针旋转，过B，C两点分别向直线l作垂线BD，CE，垂足为D，E，此时△ABD可以由△CAE通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小（取最小旋转角度）．
尝试应用如图（2），△ABC为等边三角形，直线l绕着点A顺时针旋转，D、E为直线l上两点，∠BDA＝∠AEC＝60°．△ABD可以由△CAE通过旋转变换得到吗？若可以，请指出旋转中心O的位置并说明理由；
拓展创新如图（3）在问题背景的条件下，若AB＝2，连接DC，直接写出CD的长的取值范围．
9．（2022·重庆忠县·九年级期末）已知等腰直角 SKIPIF 1 < 0 与 SKIPIF 1 < 0 有公共顶点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．现将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 旋转．
(1)如图①，当点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 在同一直线上时，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，求 SKIPIF 1 < 0 的长；
(2)如图②，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
(3)如图③，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，以 SKIPIF 1 < 0 为直角边构造等腰 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 旋转过程中，当 SKIPIF 1 < 0 最小时，直接写出 SKIPIF 1 < 0 的面积．