中考数学二轮复习考点培优专练专题三 函数综合问题（一次函数+反比例函数）（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点培优专练专题三 函数综合问题（一次函数+反比例函数）（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点培优专练专题三函数综合问题一次函数+反比例函数原卷版doc、中考数学二轮复习考点培优专练专题三函数综合问题一次函数+反比例函数解析版doc等2份试卷配套教学资源，其中试卷共128页， 欢迎下载使用。
例题（2021·黑龙江·哈尔滨市第十七中学校二模）如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣ SKIPIF 1 < 0 x+3分别交x轴，y轴于点A，B．∠OBA的外角平分线交x轴于点D．
（1）求点D的坐标；
（2）点P是线段BD上的一点（不与B，D重合），过点P作PC⊥BD交x轴于点C．设点P的横坐标为t，△BCD的面积为S，求S与t之间的函数解析式（不要求写出自变量t的取值范围）；
（3）在（2）的条件下，PC的延长线交y轴于点E，BC的延长线交DE于点F，连AP，若sin∠BAP＝ SKIPIF 1 < 0 ，求线段OF的长．
练习题
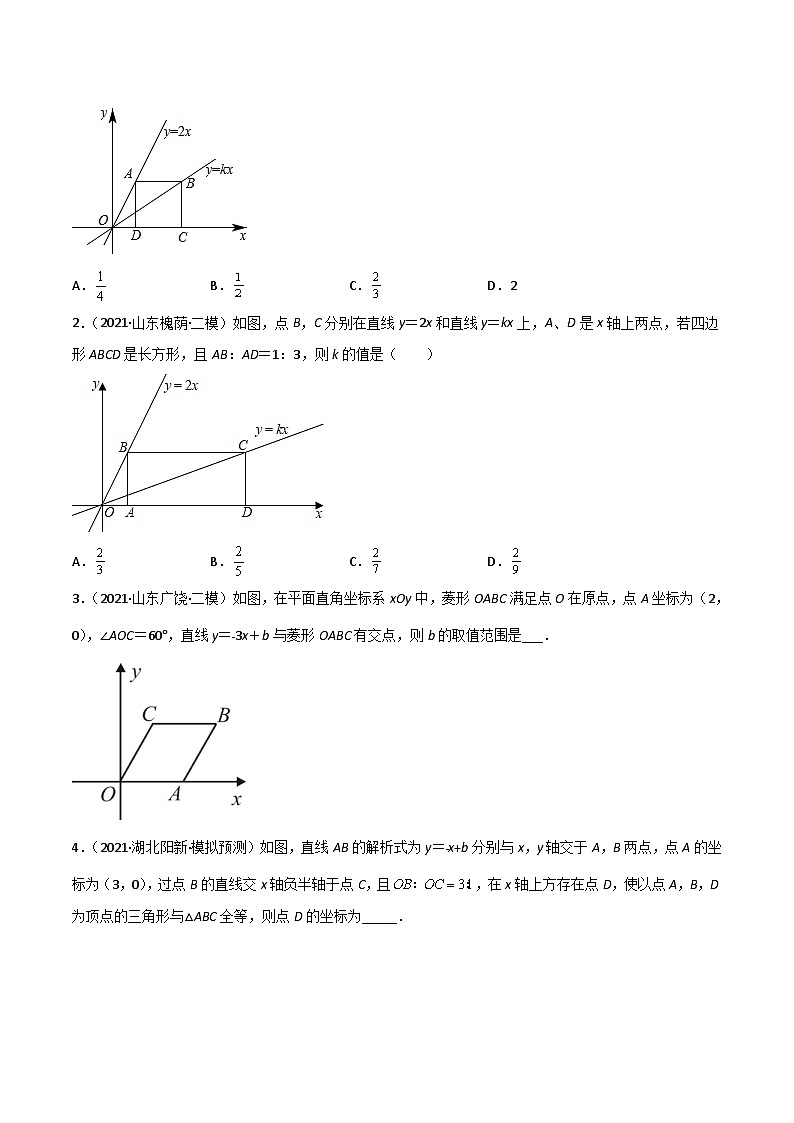
1．（2021·吉林双阳·二模）如图，在平面直角坐标系中，两条直线分别为y＝2x，y＝kx，且点A在直线y＝2x上，点B在直线y＝kx上，AB∥x轴，AD⊥x轴，BC⊥x轴垂足分别为D和C，若四边形ABCD为正方形时，则k＝（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．2
2．（2021·山东槐荫·二模）如图，点B，C分别在直线y＝2x和直线y＝kx上，A、D是x轴上两点，若四边形ABCD是长方形，且AB：AD＝1：3，则k的值是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2021·山东广饶·二模）如图，在平面直角坐标系xOy中，菱形OABC满足点O在原点，点A坐标为（2，0），∠AOC＝60°，直线y＝﹣3x＋b与菱形OABC有交点，则b的取值范围是___．
4．（2021·湖北阳新·模拟预测）如图，直线AB的解析式为y＝﹣x+b分别与x，y轴交于A，B两点，点A的坐标为（3，0），过点B的直线交x轴负半轴于点C，且 SKIPIF 1 < 0 ，在x轴上方存在点D，使以点A，B，D为顶点的三角形与△ABC全等，则点D的坐标为_____．
5．（2021·广东深圳·三模）定义：如图1，已知锐角∠AOB内有定点P，过点P任意作一条直线MN，分别交射线OA，OB于点M，N．若P是线段MN的中点时，则称直线MN是∠AOB的中点直线．如图2，射线OQ的表达式为y＝2x（x＞0），射线OQ与x轴正半轴的夹角为∠α，P（3，1），若MN为∠α的中点直线，则直线MN的表达式为__________________．
6．（2021·山东·济宁学院附属中学一模）如图，在平面直角坐标系 SKIPIF 1 < 0 中， SKIPIF 1 < 0 的顶点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的坐标分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．直线 SKIPIF 1 < 0 经过坐标原点，并与 SKIPIF 1 < 0 相交于点 SKIPIF 1 < 0 ．
(1)直接写出 SKIPIF 1 < 0 点的坐标______．
(2)若 SKIPIF 1 < 0 ，试确定点 SKIPIF 1 < 0 的坐标及直线 SKIPIF 1 < 0 的解析式．
(3)在（2）的条件下，动点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上运动，以点 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 的长为半径的 SKIPIF 1 < 0 随点 SKIPIF 1 < 0 运动，当 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的边相切时，求出 SKIPIF 1 < 0 的半径．
7．（2022·辽宁·东北育才实验学校模拟预测）如图，已知直线l1：y＝ SKIPIF 1 < 0 与直线l2：y＝﹣2x+16相交于点C，l1、l2分别交x轴于A、B两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．
(1)求△ABC的面积；
(2)求矩形DEFG的边DE与EF的长；
(3)若矩形DEFG从原地出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t（0≤t≤12）秒，矩形DEFG与△ABC重叠部分的面积为S，直接写出S关于t的函数关系式，并写出相应的t的取值范围．
8．（2021·浙江·诸暨市暨阳初级中学一模）如图，直线 SKIPIF 1 < 0 分别与x轴，y轴相交于点A，点B，作矩形ABCD，其中点C，点D在第一象限，且满足AB∶BC＝2∶1．连接BD．
（1）求点A，点B的坐标．
（2）若点E是线段AB（与端点A不重合）上的一个动点，过E作EF∥AD，交BD于点F，作直线AF．
①过点B作BG⊥AF，垂足为G，当BE＝BG时，求线段AE的长度．
②若点P是线段AD上的一个动点，连结PF，将△DFP沿PF所在直线翻折，使得点D的对应点 SKIPIF 1 < 0 落在线段BD或线段AB上．直接写出线段AE长的取值范围．
9．（2021·辽宁沈阳·中考真题）如图，平面直角坐标系中，O是坐标原点，直线 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ，与x轴交于点A，与y轴交于点B．线段 SKIPIF 1 < 0 平行于x轴，交直线 SKIPIF 1 < 0 于点D，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
（1）填空： SKIPIF 1 < 0 __________．点A的坐标是（__________，__________）；
（2）求证：四边形 SKIPIF 1 < 0 是平行四边形；
（3）动点P从点O出发，沿对角线 SKIPIF 1 < 0 以每秒1个单位长度的速度向点D运动，直到点D为止；动点Q同时从点D出发，沿对角线 SKIPIF 1 < 0 以每秒1个单位长度的速度向点O运动，直到点O为止．设两个点的运动时间均为t秒．
①当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 的面积是__________．
②当点P，Q运动至四边形 SKIPIF 1 < 0 为矩形时，请直接写出此时t的值．
10．（2021·黑龙江·哈尔滨市虹桥初级中学校模拟预测）直线 SKIPIF 1 < 0 与x轴交于A，与y轴交于C点，直线BC的解析式为 SKIPIF 1 < 0 ，与x轴交于B．
（1）如图1，求点A的横坐标；
（2）如图2，D为BC延长线上一点，过D作x轴垂线于点E，连接CE，若 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 的面积为S，求S与k的函数关系式；
（3）如图3，在（2）的条件下，连接OD交AC于点F，将 SKIPIF 1 < 0 沿CF翻折得到 SKIPIF 1 < 0 ，直线FG交CE于点K，若 SKIPIF 1 < 0 ，求点K的坐标．
二、反比例函数的综合问题
例题（2021·广东·珠海市紫荆中学三模）如图1，在平面直角坐标系xOy中，线段AB在x轴的正半轴上移动，且AB=1，过点A、B作y轴的平行线分别交函数y1＝ SKIPIF 1 < 0 （x＞0）与y2＝ SKIPIF 1 < 0 （x＞0）的图象于C、E和D、F，设点A的横坐标为m（m＞0）．
(1)D点坐标 ；F点坐标 ；连接OD、OF，则△ODF面积为 ；（用含m的代数式表示）
(2)连接CD、EF，判断四边形CDFE能否是平行四边形，并说明理由；
(3)如图2，经过点B和点G（0，6）的直线交直线AC于点H，若点H的纵坐标为正整数，请求出整数m的值．
练习题
1．（2021·河北·高阳县教育局教研室模拟预测）如图是反比例函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 在x轴上方的图象，x轴的平行线AB分别与这两个函数图象相交于点A，B，点P在x轴上．则点P从左到右的运动过程中，△APB的面积是（ ）
A．10B．4
C．5D．从小变大再变小
2．（2021·山东滨州·一模）如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB＝ SKIPIF 1 < 0 ，反比例函数y＝ SKIPIF 1 < 0 在第一象限内的图象经过点A，与BC交于点F，则点F的坐标为（ ）
A．（ SKIPIF 1 < 0 ﹣1，4 SKIPIF 1 < 0 ﹣20）B．（ SKIPIF 1 < 0 +1，4 SKIPIF 1 < 0 ﹣20）
C．（ SKIPIF 1 < 0 +5， SKIPIF 1 < 0 ）D．（ SKIPIF 1 < 0 ﹣9， SKIPIF 1 < 0 ）
3．（2021·山东济南·二模）如图，在平面直角坐标系中，菱形ABCD的对称中心恰好是原点O，已知点B坐标是 SKIPIF 1 < 0 ，双曲线y= SKIPIF 1 < 0 经过点A，则菱形ABCD的面积是( )
A．9 SKIPIF 1 < 0 B．18C． SKIPIF 1 < 0 D．25
4．（2021·广东深圳·三模）如图，在反比例函数y＝ SKIPIF 1 < 0 （x＞0）的图象上有动点A，连接OA，y＝ SKIPIF 1 < 0 （x＞0）的图象经过OA的中点B，过点B作BC∥x轴交函数y＝ SKIPIF 1 < 0 的图象于点C，过点C作CE∥y轴交函数y＝ SKIPIF 1 < 0 的图象于点D，交x轴点E，连接AC，OC，BD，OC与BD交于点F．下列结论：①k＝1；②S△BOC＝ SKIPIF 1 < 0 ；③S△CDF＝ SKIPIF 1 < 0 S△AOC；④若BD＝AO，则∠AOC＝2∠COE．其中正确的是（ ）
A．①③④B．②③④C．①②④D．①②③④
5．（2021·江苏扬州·一模）如图，正方形的顶点A，C分别在y轴和x轴上，边BC的中点F在y轴上，若反比例函数 SKIPIF 1 < 0 的图象恰好经过CD的中点E，则OA的长为______．
6．（2021·福建·厦门五缘实验学校二模）如图，在平面直角坐标系中，反比例函数y SKIPIF 1 < 0 （k＞0）的图象与半径为5的⊙O交于M、N两点，△MON的面积为3.5，若动点P在x轴上，则PM+PN的最小值是______．
7．（2021·江苏常州·二模）如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数y＝ SKIPIF 1 < 0 （k＞0，x＞0）的图象上，CD在x轴上，点B在y轴上，已知CD＝2．
(1)点A是否在该反比例函数的图象上？请说明理由；
(2)若该反比例函数图象与DE交于点Q，求点Q的横坐标．
8．（2021·山东菏泽·三模）如图，反比例函数 SKIPIF 1 < 0 的图像过等边 SKIPIF 1 < 0 的顶点B， SKIPIF 1 < 0 ，点A在反比例函数的图象上，连接AC，AO．
(1)求反比例函数 SKIPIF 1 < 0 的表达式；
(2)若四边形ACBO的面积是 SKIPIF 1 < 0 ，求点A的坐标．
9．（2021·吉林·三模）如图，在平面直角坐标系中，矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上，顶点B的坐标为（4，2），双曲线 SKIPIF 1 < 0 （x＞0）的图象交BC于点D，若BD＝ SKIPIF 1 < 0 ．求反比例函数的解析式及点F的坐标．
10．（2022·广东江门·一模）反比例函数y1＝ SKIPIF 1 < 0 （k1＞0）和y2＝ SKIPIF 1 < 0 在第一象限的图象如图所示，过原点的两条射线分别交两个反比例图象于A，D和B，C
(1)求证：AB∥CD；
(2)若k1＝2，S△OAB＝2，S四边形ABCD＝3，求反比例函数y2＝ SKIPIF 1 < 0 （k2＞0）的解析式．
11．（2021·湖北恩施·模拟预测）如图，在平面直角坐标系中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 轴、 SKIPIF 1 < 0 轴上的一动点，以 SKIPIF 1 < 0 为边向外作矩形 SKIPIF 1 < 0 ，对角线BD∥x轴，反比例函数 SKIPIF 1 < 0 图象经过矩形对角线交点 SKIPIF 1 < 0 ．
(1)如图1，若点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 坐标分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长；
(2)如图2，保持点 SKIPIF 1 < 0 坐标 SKIPIF 1 < 0 不变，点 SKIPIF 1 < 0 向右移移动，当点 SKIPIF 1 < 0 刚好在反比函数图象上时，求点 SKIPIF 1 < 0 坐标及 SKIPIF 1 < 0 的值．
12．（2021·广东·汕头市潮南实验学校一模）如图，在平面直角坐标系中，点 SKIPIF 1 < 0 为坐标系原点，矩形 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别在 SKIPIF 1 < 0 轴和 SKIPIF 1 < 0 轴上，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．已知反比例函数 SKIPIF 1 < 0 的图象经过 SKIPIF 1 < 0 边上的中点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的值；
(2)猜想 SKIPIF 1 < 0 的面积与 SKIPIF 1 < 0 的面积之间的关系，请说明理由．
(3)若点 SKIPIF 1 < 0 在该反比例函数的图象上运动（不与点 SKIPIF 1 < 0 重合），过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 所在直线于点 SKIPIF 1 < 0 ，记四边形 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的解析式并写出 SKIPIF 1 < 0 的取值范围．
13．（2021·重庆北碚·模拟预测）有这样一个问题：探究函数y＝ SKIPIF 1 < 0 的图象与性质，小童根据学习函数的经验，对函数的图象与性质进行例研究，已知当x＝2时，y＝7， SKIPIF 1 < 0 时，y＝﹣3．下面是小童探究的过程，请补充完整：
(1)该函数的解析式为 ，m＝ ，n＝ ．
根据图中描出的点，画出函数图象．
(2)根据函图象，下列关于函数性质的描述正确的是 ；
①该函数图象是中心对称图形，它的对称中心是原点．
②该函数既无最大值也无最小值．
③在自变量的取值范围内，y随x的增大而减小．
(3)请结合（1）中函数图象，直接写出关于x的不等式 SKIPIF 1 < 0 的解集．（保留1位小数，误差不超过0.2）
14．（2021·广东·二模）如图1，点P是反比例函数y＝ SKIPIF 1 < 0 （k＞0）在第一象限的点，PA⊥y轴于点A，PB⊥x轴于点B，反比例函数y＝ SKIPIF 1 < 0 的图象分别交线段AP、BP于C、D，连接CD，点G是线段CD上一点．
(1)若点P（6，3），求△PCD的面积；
(2)在（1）的条件下，当PG平分∠CPD时，求点G的坐标；
(3)如图2，若点G是OP与CD的交点，点M是线段OP上的点，连接MC、MD．当∠CMD＝90°时，求证：MG＝ SKIPIF 1 < 0 CD．
15．（2021·广东珠海·一模）如图，在平面直角坐标系中， SKIPIF 1 < 0 为坐标原点，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴正半轴上，四边形 SKIPIF 1 < 0 为平行四边形， SKIPIF 1 < 0 ，反比例函数 SKIPIF 1 < 0 的图象在第一象限内过点 SKIPIF 1 < 0 ，且经过 SKIPIF 1 < 0 边的中点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)当 SKIPIF 1 < 0 时，求反比例函数的表达式；
(2)在（1）的条件下，求点 SKIPIF 1 < 0 的坐标；
(3)证明： SKIPIF 1 < 0 ．
三、一次函数与反比例函数的综合问题
例题（2021·江苏·苏州市吴中区碧波中学一模）如图，过直线 SKIPIF 1 < 0 上一点P作 SKIPIF 1 < 0 轴于点D，线段 SKIPIF 1 < 0 交函数 SKIPIF 1 < 0 的图象于点C，点C为线段 SKIPIF 1 < 0 的中点，点C关于直线 SKIPIF 1 < 0 的对称点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ．
（1）直接写出点C的坐标（____，______），求k、m的值：
（2）求直线 SKIPIF 1 < 0 函数 SKIPIF 1 < 0 图象的交点坐标；
（3）直接写出不等式 SKIPIF 1 < 0 的解集．
练习题
1．（2021·四川成都·一模）如图，在同一平面直角坐标系中，反比例函数y＝ SKIPIF 1 < 0 与一次函数y＝kx﹣k（k为常数，且k≠0）的图象可能是（ ）
A．B．C．D．
2．（2021·湖北荆门·中考真题）在同一直角坐标系中，函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的大致图象是（ ）
A．①②B．②③C．②④D．③④
3．（2022·湖北武汉·模拟预测）如图，直线y＝x+8分别交x、y轴于A、B两点，交双曲线 SKIPIF 1 < 0 ，若CD＝3（AC+BD），则k的值为（ ）
A．﹣6B．﹣7C．﹣8D．﹣9
4．（2021·广东·深圳市罗湖区翠园初级中学二模）将反比例函数y＝ SKIPIF 1 < 0 的图象绕坐标原点O逆时针旋转30°，得到如图的新曲线A（﹣3，3 SKIPIF 1 < 0 ），B（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）的直线相交于点C、D，则△OCD的面积为（ ）
A．3B．8C．2 SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2018·山东青岛·中考模拟）如图，反比例函数y＝ SKIPIF 1 < 0 （x＜0）与一次函数y＝x＋4的图象交于A、B两点的横坐标分别为－3，－1．则关于x的不等式 SKIPIF 1 < 0 ＜x＋4（x＜0）的解集为（ ）
A．x＜－3B．－3＜x＜－1C．－1＜x＜0D．x＜－3或－1＜x＜0
6．（2021·山东临沂·一模）在平面直角坐标系 SKIPIF 1 < 0 中，已知一次函数 SKIPIF 1 < 0 与反比例函数 SKIPIF 1 < 0 的图象交于点 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 关于x轴的对称点为点 SKIPIF 1 < 0 ．
(1)求这两个函数的表达式．
(2)直接写出关于x的不等式 SKIPIF 1 < 0 的解．
(3)过点B作y轴的垂线与直线AC交于点D，经过点C的直线与直线BD交于点E，且 SKIPIF 1 < 0 ，直接写出点E的横坐标 SKIPIF 1 < 0 的取值范围．
7．（2021·山东青岛·一模）如图，直线y1＝k1x+b与双曲线y2＝ SKIPIF 1 < 0 在第一象限内交于A、B两点，已知A（1，m），B（2，1）．
(1)分别求出直线和双曲线的解析式；
(2)设点P是线段AB上的一个动点，过点P作PD⊥x轴于点D，E是y轴上一点，当△PED的面积最大时，请直接写出此时P点的坐标为 ．
8．（2021·广东清远·二模）如图，一次函数y1＝k1x+4与反比例函数 SKIPIF 1 < 0 的图象交于点A(2,m)和B(-6,-2)，与y轴交于点C．
(1)求一次函数与反比例函数的表达式；
(2)过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点，设直线OP与线段AD交于点E，当S四边形ODAC:S△ODE＝4:1时，求点P的坐标；
(3)点M是y轴上的一个动点，当△MBC为直角三角形时，直接写出点M的坐标．
9．（2021·湖南·株洲市芦淞区教育教学研究指导中心模拟预测）如图1，点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，反比例函数 SKIPIF 1 < 0 ＞0）的图象经过点B．
(1)求反比例函数解析式；
(2)将线段AB向右平移 SKIPIF 1 < 0 个单位长度（ SKIPIF 1 < 0 ＞0），得到对应线段CD，连接AC、BD．
①如图2，当 SKIPIF 1 < 0 ＝3时，过D作DF⊥ SKIPIF 1 < 0 轴于点F，交反比例函数图象于点E，求E点坐标；
②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三角形，求所有满足条件的 SKIPIF 1 < 0 的值．
10．（2021·四川·叙州区双龙镇初级中学校模拟预测）如图1，在平面直角坐标系中，直线l1：y＝kx+b（k≠0）与双曲线 SKIPIF 1 < 0 交于点A（a，4a）（a＞0）和点B（﹣4，n），连接OA，OB，其中 SKIPIF 1 < 0 ．
(1)求双曲线和直线l1的表达式；
(2)求△AOB的面积；
(3)如图2，将直线l1：y＝kx+b沿着y轴向下平移得到直线l2，且直线l2与双曲线在第三象限内的交点为C，若△ABC的面积为20，求直线l2与y轴的交点坐标．
11．（2021·山东潍坊·二模）如图，在平面直角坐标系 SKIPIF 1 < 0 中，函数 SKIPIF 1 < 0 的图象与直线 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值；
(2)已知点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作平行于 SKIPIF 1 < 0 轴的直线，交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作平行于 SKIPIF 1 < 0 轴的直线，交函数 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象于点 SKIPIF 1 < 0 ．
①当 SKIPIF 1 < 0 时，判断线段 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系，并说明理由；
②若 SKIPIF 1 < 0 ，结合函数的图象，直接写出 SKIPIF 1 < 0 的取值范围．
12．（2021·四川南充·一模）如图，直线y＝kx+b与x轴交于点A，与y轴交于点B，与双曲线y＝ SKIPIF 1 < 0 （x＜0）交于C（﹣8，1），D（﹣m，m2）两点．
(1)求直线和双曲线的解析式；
(2)比较AC和BD的大小，直接填空：AC BD；
(3)写出直线对应函数值大于双曲线对应函数值自变量x的取值范围，直接填空： ．
13．（2021·山东临沂·一模）如图，反比例函数 SKIPIF 1 < 0 ( SKIPIF 1 < 0 ，x＞0)的图象与直线y=3x相交于点C，过直线上点A(1，3)作AB⊥x轴于点B，交反比例函数图象于点D，且AB=3BD．
(1)求k的值；
(2)求点C的坐标；
(3)在y轴上确定一点M，使点M到C，D两点距离之和d=MC+MD最小，求点M的坐标．
14．（2021·广东·东莞市南开实验学校一模）如图，一次函数y=k1x+1的图象与反比例函数 SKIPIF 1 < 0 点的图象相交于A、B两点，点C在x轴正半轴上，点D（1，-2 ），连接OA、OD、DC、AC，四边形OACD为菱形．
(1)求一次函数与反比例函数的解析式；
(2)根据图象，直接写出反比例函数值大于一次函数值时，x的取值范围；
(3)设点P是直线AB上一动点，且S△OAP= SKIPIF 1 < 0 S菱形OACD，求点P的坐标．
15．（2021·山东济南·三模）已知点A（0，4），将点A先向右平移1个单位长度，再向上平移2个单位长度，对应点B恰好落在反比例函数 SKIPIF 1 < 0 的图象上．过点B的直线l的表达式为y＝mx+n，与反比例函数图象的另一个交点为点C，分别交x轴、y轴于点D、点E．
(1)求反比例函数表达式；
(2)若线段BC＝2CD，求△BOD的面积；
(3)在（2）的条件下，点P为反比例函数图象上B、C之间的一点（不与B、C重合），PM⊥x轴交直线l于点M，PN⊥y轴交直线l于点N，请分析EM•DN是否为定值，并说明理由．
16．（2021·广东阳江·一模）如图，一次函数y＝kx+b（k≠0）与反比例函数 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 （4， SKIPIF 1 < 0 ），B（1，2），AC⊥x轴于点C，BD⊥y轴于点D．
(1)根据图象直接回答：在第一象限内，当x取何值时，一次函数值大于反比例函数值；
(2)求一次函数的解析式及m的值；
(3)P是线段AB上的一点，连接PC，PD，若△BDP∽△ACP，求点P的坐标．
17．（2021·广东佛山·二模）如图，一次函数y＝k1x+b与反比例函数y＝ SKIPIF 1 < 0 图象交于点B（﹣1，6）、点A，且点A的纵坐标为3．
(1)填空：k1＝ ，b＝ ；k2＝ ；
(2)结合图形，直接写出k1x+b＞ SKIPIF 1 < 0 时x的取值范围；
(3)在梯形ODCA中，AC SKIPIF 1 < 0 OD，且下底DO在x轴上，CD⊥x轴于点D，CD和反比例函数的图象交于点M，当梯形ODCA的面积为12时，求此时点M坐标．
18．（2021·广东梅州·一模）已知一次函数y＝kx＋b与反比例函数y＝ SKIPIF 1 < 0 的图象交于A（﹣3，2）、B（1，n）两点．
（1）求一次函数和反比例函数的表达式；
（2）△AOB的面积为 ；
（3）直接写出不等式kx＋b＞ SKIPIF 1 < 0 的解 ；
（4）点P在x的负半轴上，当△PAO为等腰三角形时，直接写出点P的坐标．
19．（2021·江苏南通·中考真题）定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”．例如，点 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的图象的“等值点”．
（1）分别判断函数 SKIPIF 1 < 0 的图象上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；
（2）设函数 SKIPIF 1 < 0 的图象的“等值点”分别为点A，B，过点B作 SKIPIF 1 < 0 轴，垂足为C．当 SKIPIF 1 < 0 的面积为3时，求b的值；
（3）若函数 SKIPIF 1 < 0 的图象记为 SKIPIF 1 < 0 ，将其沿直线 SKIPIF 1 < 0 翻折后的图象记为 SKIPIF 1 < 0 ．当 SKIPIF 1 < 0 两部分组成的图象上恰有2个“等值点”时，直接写出m的取值范围．
x
…
﹣4
﹣3
﹣2
0
2
3
4
…
y
…
m
SKIPIF 1 < 0
SKIPIF 1 < 0
﹣3
7
n
SKIPIF 1 < 0
…