中考数学二轮复习考点培优专练专题十 圆的综合问题（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点培优专练专题十 圆的综合问题（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点培优专练专题十圆的综合问题原卷版doc、中考数学二轮复习考点培优专练专题十圆的综合问题解析版doc等2份试卷配套教学资源，其中试卷共167页， 欢迎下载使用。
例题1如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，以 SKIPIF 1 < 0 为直径的 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 是 SKIPIF 1 < 0 的切线．
(2)求证： SKIPIF 1 < 0 ．
(3)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的半径长．
练习题
1．在△ABC中，∠ACB＝90°，以BC为直径的⊙O交AB于点D．
(1)如图①，以点B为圆心，BC为半径作圆弧交AB于点M，连结CM，若∠ABC＝66°，求∠ACM；
(2)如图②，过点D作⊙O的切线DE交AC于点E，求证：AE＝EC；
(3)如图③，在（1）（2）的条件下，若tanA＝ SKIPIF 1 < 0 ，求S△ADE：S△ACM的值．
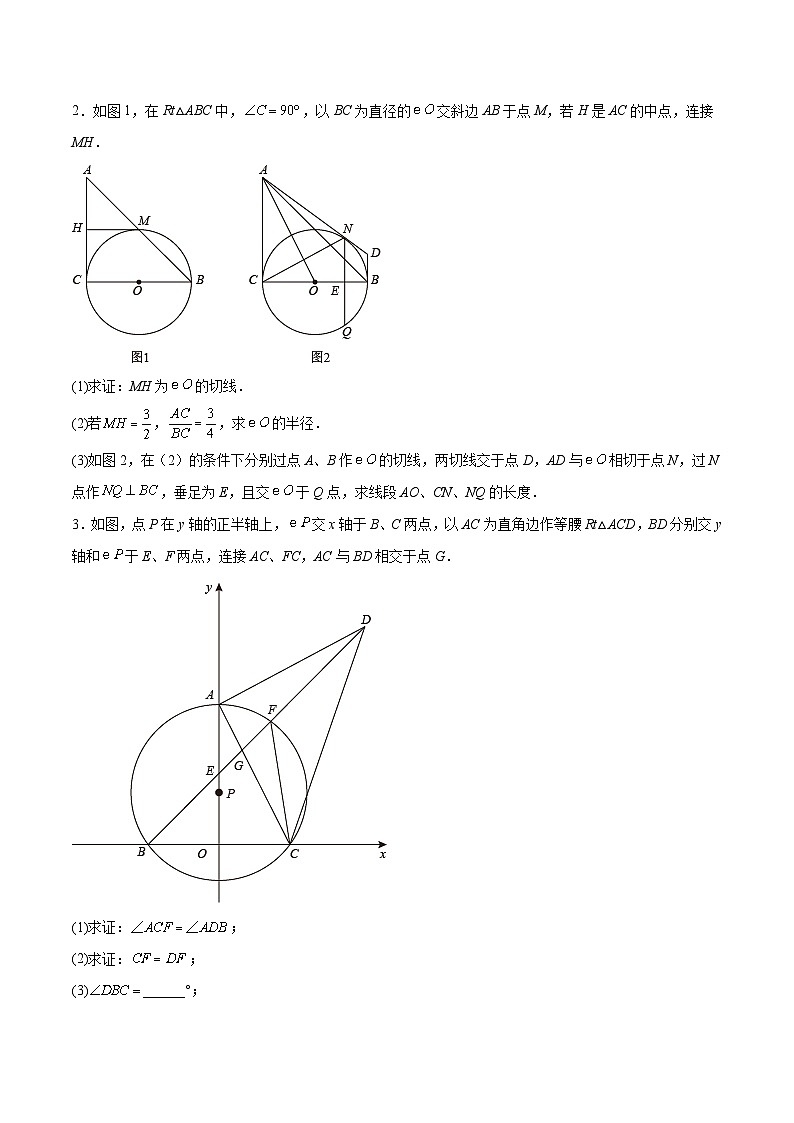
2．如图1，在Rt△ABC中， SKIPIF 1 < 0 ，以BC为直径的 SKIPIF 1 < 0 交斜边AB于点M，若H是AC的中点，连接MH．
(1)求证：MH为 SKIPIF 1 < 0 的切线．
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的半径．
(3)如图2，在（2）的条件下分别过点A、B作 SKIPIF 1 < 0 的切线，两切线交于点D，AD与 SKIPIF 1 < 0 相切于点N，过N点作 SKIPIF 1 < 0 ，垂足为E，且交 SKIPIF 1 < 0 于Q点，求线段AO、CN、NQ的长度．
3．如图，点P在y轴的正半轴上， SKIPIF 1 < 0 交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和 SKIPIF 1 < 0 于E、F两点，连接AC、FC，AC与BD相交于点G．
(1)求证： SKIPIF 1 < 0 ；
(2)求证： SKIPIF 1 < 0 ；
(3) SKIPIF 1 < 0 ______°；
(4)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则△GDC的面积为______．
4．如图，四边形 SKIPIF 1 < 0 内接于半圆 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是半圆 SKIPIF 1 < 0 的直径， SKIPIF 1 < 0 是半圆 SKIPIF 1 < 0 的切线， SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 并延长交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 ．
(2)探究 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系．
(3)求 SKIPIF 1 < 0 的值．
5．【概念提出】圆心到弦的距离叫做该弦的弦心距．
【数学理解】如图①，在 SKIPIF 1 < 0 中，AB是弦， SKIPIF 1 < 0 ，垂足为P，则OP的长是弦AB的弦心距．
(1)若 SKIPIF 1 < 0 的半径为5，OP的长为3，则AB的长为______．
(2)若 SKIPIF 1 < 0 的半径确定，下列关于AB的长随着OP的长的变化而变化的结论：
①AB的长随着OP的长的增大而增大；②AB的长随着OP的长的增大而减小；③AB的长与OP的长无关．
其中所有正确结论的序号是______．
(3)【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为______°．
(4)已知如图②给定的线段EF和 SKIPIF 1 < 0 ，点Q是 SKIPIF 1 < 0 内一定点．过点Q作弦AB，满足 SKIPIF 1 < 0 ，请问这样的弦可以作______条．
6．已知 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的外接圆， SKIPIF 1 < 0 ．
(1)如图1，延长 SKIPIF 1 < 0 至点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
①求证： SKIPIF 1 < 0 为直角三角形；
②若 SKIPIF 1 < 0 的半径为4， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
(2)如图2，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的一点，且点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 位于 SKIPIF 1 < 0 两侧，作 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称的图形 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，试猜想 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三者之间的数量关系并给予证明．
7．定义：两个角对应互余，且这两个角的夹边对应相等的两个三角形叫做余等三角形．如图1，在△ABC和△DEF中，若∠A+∠E＝∠B+∠D＝90°，且AB＝DE，则△ABC和△DEF是余等三角形．
(1)图2，等腰直角△ABC，其中∠ACB＝90°，AC＝BC，点D是AB上任意一点（不与点A，B重合），则图中△________和△________是余等三角形，并求证：AD2+BD2＝2CD2．
(2)图3，四边形ABCD是⊙O的内接四边形，⊙O的半径为5，且AD2+BC2＝100，
①求证：△ABC和△ADC是余等三角形．
②图4，连接BD交AC于点I，连接OI，E为AI上一点，连接EO并延长交BI于点F，若∠ADB＝67.5°，IE＝IF，设OI＝x，S△EIF＝y，求y关于x的函数关系式．
8．如图1，在等腰 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点D是线段 SKIPIF 1 < 0 上一点，以 SKIPIF 1 < 0 为直径作 SKIPIF 1 < 0 ， SKIPIF 1 < 0 经过点A．
(1)求证： SKIPIF 1 < 0 是 SKIPIF 1 < 0 的切线；
(2)如图2，过点A作 SKIPIF 1 < 0 垂足为E，点F是 SKIPIF 1 < 0 上任意一点，连结 SKIPIF 1 < 0 ．
①如图2，当点F是 SKIPIF 1 < 0 的中点时，求 SKIPIF 1 < 0 的值；
②如图3，当点F是 SKIPIF 1 < 0 上的任意一点时， SKIPIF 1 < 0 的值是否发生变化？请说明理由．
(3)在（2）的基础上，若射线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的另一交点G，连结 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时，直接写出 SKIPIF 1 < 0 的值．
9．【证明体验】
（1）如图1，过圆上一点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 切线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是弦（不是直径），若 SKIPIF 1 < 0 是直径，连接 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
（2）如图2，若 SKIPIF 1 < 0 不是直径， SKIPIF 1 < 0 ______ SKIPIF 1 < 0 （填“＞”、“