中考数学二轮复习考点培优专练专题一 规律探究问题（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点培优专练专题一 规律探究问题（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点培优专练专题一规律探究问题原卷版doc、中考数学二轮复习考点培优专练专题一规律探究问题解析版doc等2份试卷配套教学资源，其中试卷共94页， 欢迎下载使用。
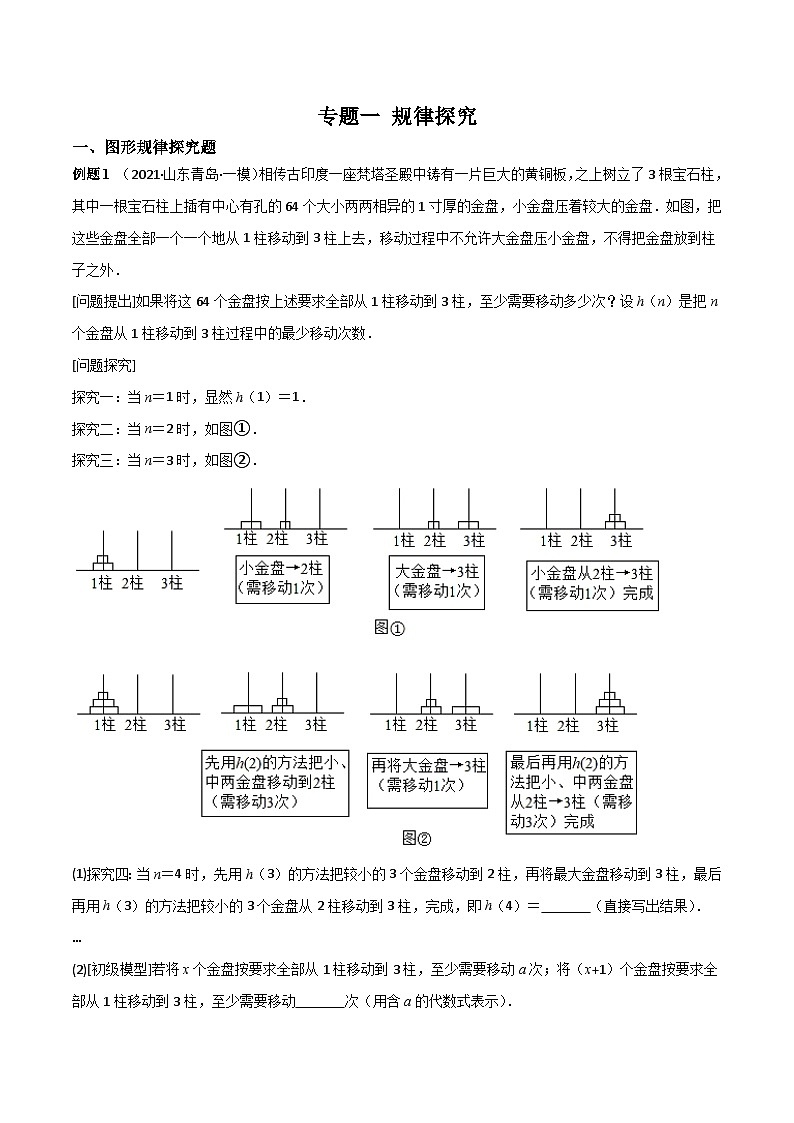
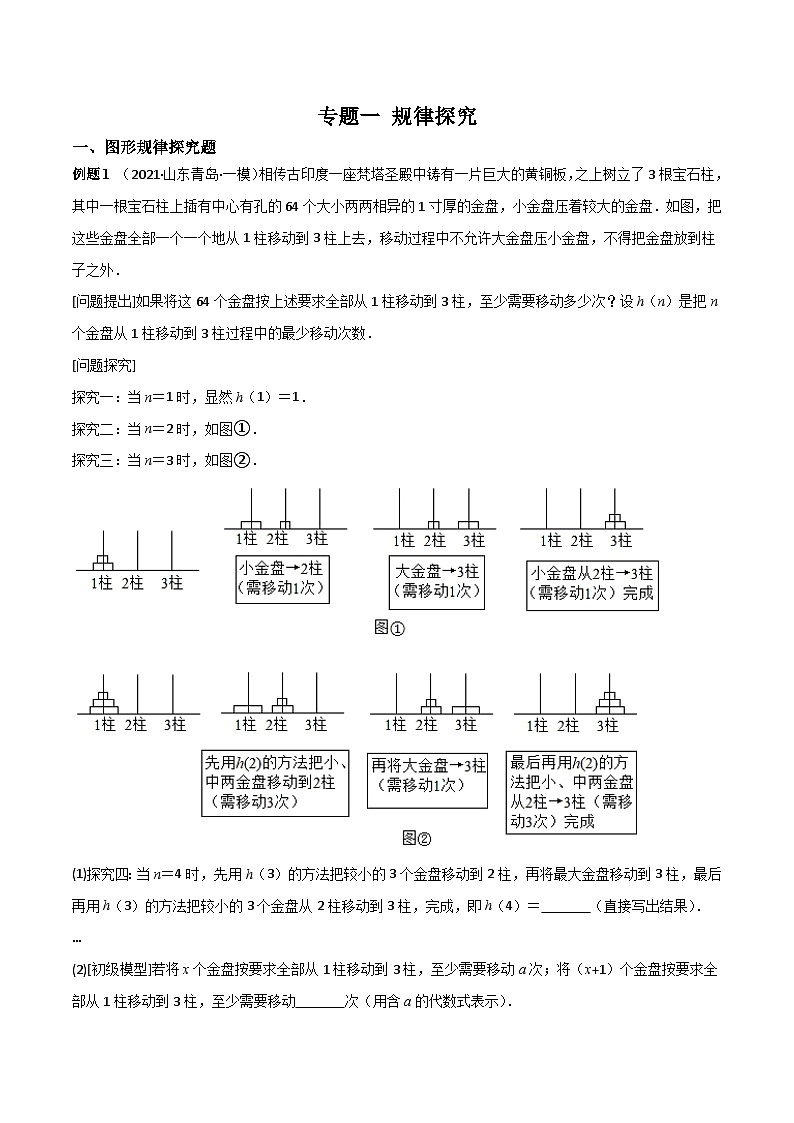
例题1 （2021·山东青岛·一模）相传古印度一座梵塔圣殿中铸有一片巨大的黄铜板，之上树立了3根宝石柱，其中一根宝石柱上插有中心有孔的64个大小两两相异的1寸厚的金盘，小金盘压着较大的金盘．如图，把这些金盘全部一个一个地从1柱移动到3柱上去，移动过程中不允许大金盘压小金盘，不得把金盘放到柱子之外．
[问题提出]如果将这64个金盘按上述要求全部从1柱移动到3柱，至少需要移动多少次？设h（n）是把n个金盘从1柱移动到3柱过程中的最少移动次数．
[问题探究]
探究一：当n＝1时，显然h（1）＝1．
探究二：当n＝2时，如图①．
探究三：当n＝3时，如图②．
(1)探究四：当n＝4时，先用h（3）的方法把较小的3个金盘移动到2柱，再将最大金盘移动到3柱，最后再用h（3）的方法把较小的3个金盘从2柱移动到3柱，完成，即h（4）＝ （直接写出结果）．
…
(2)[初级模型]若将x个金盘按要求全部从1柱移动到3柱，至少需要移动a次；将（x+1）个金盘按要求全部从1柱移动到3柱，至少需要移动 次（用含a的代数式表示）．
(3)[自主探究]仿照“问题探究”中的方法，将6个金盘按要求全部从1柱移动到3柱，至少需要多少次？（写出必要的计算过程．）
(4)[最终模型]综合收集到的数据探索规律可知：将64个金盘按上述要求全部从1柱移动到3柱，至少需要移动 次．
(5)[问题变式]若在原来条件的基础上，再添加1个条件：每次只能将金盘向相邻的柱子移动（即：2柱的金盘可以移动到1柱或3柱，但1柱或3柱的金盘只能移动到2柱），则移动完64个金盘至少需要移动 次．
练习题
1．（2021·山东蒙阴·三模）下列图形是由同样大小的围棋棋子按照一定规律摆成的“山”字，其中第①个“山”字中有7颗棋子，第②个“山”字中有12颗棋子，第③个“山”字中有17颗棋子，…，按照此规律，第⑥个“山”字中棋子颗数为（ ）颗．
A．32B．37C．22D．42
2．（2021·重庆十八中模拟预测）下列图形都是由同样大小的黑点按一定规律组成的，其中第①个图形中一共有3个黑点，第②个图形中一共有8个黑点，……，则第⑧个图形中黑点的个数是（ ）
A．29B．38C．48D．593．（2022·重庆·一模）如图，第①个图形中共有4个小黑点，第②个图形中共有7个小黑点，第③个图形中共有10个小黑点，第④个图形中共有13个小黑点，……，按此规律排列下去，则第⑥个图形中小黑点的个数为（ ）
A．19B．20C．22D．25
4．（2021·山东省日照市实验中学二模）如图，将△ABC沿着过BC，AB的中点D，E所在的直线折叠，使点B落在AC边上的B1处，称为第一次操作，点D到AC的距离为h1；还原纸片后，再将△BDE沿着过BD，BE的中点D1，E1所在的直线折叠，使点B落在DE边上的B2处，称为第二次操作，点D1到AC的距离记为h2；按上述方法不断操作下去，…，经过第n次操作后得到点Dn﹣1到AC的距离记为hn．若h1＝1，则hn值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2021·湖南师大附中博才实验中学一模）如图：上述图形是由同样大小的棋子按照一定规律排列而成的，其中图1中有5个棋子，图2中有10个棋子，图3中有16个棋子，…，则图4中有_________个棋子．
6．（2021·河南武陟·一模）如图，某图书阅览室摆放桌椅如下：按此规律摆放，2n+1（n是不小于4的自然数）人需要 ________张桌子．
7．（2021·内蒙古东胜·二模）如图，在平面直角坐标系中， SKIPIF 1 < 0 将 SKIPIF 1 < 0 绕A顺时针旋转得到 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ﹔将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 顺时针旋转得到 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 继续顺时针旋转，此时 SKIPIF 1 < 0 …按此规律继续旋转，直至得到点 SKIPIF 1 < 0 为止，则 SKIPIF 1 < 0 _________．
8．（2021·山东博山·二模）德国数学家康托尔引入位于一条线段上的一些点的集合，做如下：
取一条长度为1的线段三等分后，去掉中间段，余下两条线段，达到第1阶段；
将剩下的两条线段分别三等分后，各去掉中间段，余下四条线段，达到第2阶段；
再将剩下四条线段分别等三等分后，各去掉中间段，余下八条线段，达到第3阶段；
…，
一直如此操作下去，在不断分割舍弃过程中，所形成的线段数目越来越多．
如图是最初几个阶段，当达到第n个阶段时（n为正整数），去掉的线段的长度之和为_____．（用含n的式子表示）
9．（2021·台湾·模拟预测）凯特平时常用底面为矩形的模具制作蛋糕，并以平行于模具任一边的方式进行横切或纵切，横切都是从模具的左边切割到模具的右边，纵切都是从模具的上边切割到模具的下边 SKIPIF 1 < 0 用这种方式，可以切出数个大小完全相同的小块蛋糕 SKIPIF 1 < 0 在切割后，他发现小块蛋糕接触模具的地方外皮比较焦脆，以如图为例，横切2刀，纵切3刀，共计5刀，切出 SKIPIF 1 < 0 个小块蛋糕，其中侧面有焦脆的小块蛋糕共有10个，所有侧面都不焦脆的小块蛋糕共有2个．
请根据上述切割方式，回答下列问题，并详细解释或完整写出你的解题过程：
（1）若对一块蛋糕切了4刀，则可切出几个小块蛋糕？请写出任意一种可能的蛋糕块数即可．
（2）今凯特根据一场聚餐的需求，打算制作出恰好60个所有侧面都不焦脆的小块蛋糕，为了避免劳累并加快出餐速度，在不超过20刀的情况下，请问凯特需要切几刀，才可以达成需求？请写出所有可能的情形．
10．（2022·山东青岛·模拟预测）问题提出：如图1，在 SKIPIF 1 < 0 个小正方体组成的长方体中，最多能看到多少个小正方体？
研究思路：直接研究这个问题较为复杂，我们可以将问题转化为用小正方体总数减去看不到的小正方体个数，以求得最多能看到的小正方体的个数．
探究一：如图2，在 SKIPIF 1 < 0 的正方体中，有 SKIPIF 1 < 0 个小正方体看不到，所以最多能看到 SKIPIF 1 < 0 个小正方体．
探究二：在 SKIPIF 1 < 0 的正方体中，有 SKIPIF 1 < 0 个小正方体看不到，所以最多能看到 SKIPIF 1 < 0 个小正方体．
(1)探究三：在 SKIPIF 1 < 0 的正方体中，有 SKIPIF 1 < 0 个小正方体看不到，所以最多能看到 个小正方体．
(2)探究四：在 SKIPIF 1 < 0 的正方体中，有 个小正方体看不到，所以最多能看到 个小正方体．（均化为最简形式）
(3)问题解决：如图3，小明是魔方爱好者，他有一个七阶魔方（ SKIPIF 1 < 0 的正方体），则他最多能看到 个小正方体．
(4)问题应用：若在 SKIPIF 1 < 0 的正方体中最多能看到217个小正方体，求n的值．（写出解答过程）
(5)探究五：在 SKIPIF 1 < 0 的长方体中，有 SKIPIF 1 < 0 个小正方体看不到，所以最多能看到 个小正方体．
(6)探究六：在 SKIPIF 1 < 0 的长方体中，最多能看到 个小正方体．（化为最简形式）
(7)拓展延伸：小明在研究 SKIPIF 1 < 0 的长方体时，他最多能看到a个小正方体，此时他看不到12个小正方体，则a有 种可能取值，a的最小值是 ．
11．（2021·山东青岛·三模）【问题提出】
每对小兔子在出生后1个月就长成大兔子，而每对大兔子每个月能生出1对小兔子来，如果1个人在1月份买了1对小兔子，假设每对兔子均可成活，且具有繁殖能力，那么理论上12月份的时候他共有多少对兔子？
(1)【问题探究】
1月份，有1对小兔子；
2月份，长成大兔子，所以还是1对；
3月份，大兔子生下1对小兔子，所以共有2对；
4月份，刚生下的小兔子长成大兔子，而原来的大兔子又生下1对小兔子，共3对；
…
依此类推，请填下表：
(2)【类比应用】
树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵苗在1年后长出1条新枝，第2年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过1年的同时萌发新枝，当年生的新枝则依次“休息”，这在生物学上称为“鲁德维格定律”．那么，10年后树上有 条树枝．
(3)【综合应用】
如图①，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有 种回家的方法；
(4)如图②，在正五边形ABCDE上，一只青蛙从点A开始跳动，每次可以随意跳到相邻两个顶点中的一个上，跳到点D上就停止跳动．青蛙在6次之内（含6次）跳到点D有 种不同的跳法．
二、数字规律探究题
例题2（2021·山东·青岛经济技术开发区第四中学一模）阅读下面的材料：
按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项，排在第一位的数称为第一项，记为 SKIPIF 1 < 0 ，排在第二位的数称为第二项，记为 SKIPIF 1 < 0 ，依次类推，排在第 SKIPIF 1 < 0 位的数称为第 SKIPIF 1 < 0 项，记为 SKIPIF 1 < 0 ．所以，数列的一般形式可以写成： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用 SKIPIF 1 < 0 表示．如：数列 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,…为等差数列，其中 SKIPIF 1 < 0 ,公差 SKIPIF 1 < 0 ．
根据以上材料，解答下列问题：
(1)等差数列 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,…的公差 SKIPIF 1 < 0 为________，第 SKIPIF 1 < 0 项是________．
(2)如果一个数列 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是等差数列，且公差为 SKIPIF 1 < 0 ，那么根据定义可得到： SKIPIF 1 < 0 , SKIPIF 1 < 0
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 .
由此，请你填空完成等差数列的通项公式： SKIPIF 1 < 0 （_____）d．
(3) SKIPIF 1 < 0 是不是等差数列 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的项？如果是，是第几项？
练习题
1．（2021·山东济宁·中考真题）按规律排列的一组数据： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，□， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…，其中□内应填的数是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2021·湖北十堰·中考真题）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（ ）
A．2025B．2023C．2021D．2019
3．（2021·山东沂水·一模）观察下列两行数：
0，2，4，6，8，10，12，14，16，…
0，3，6，9，12，15，18，21，24，…
探究发现：第1个相同的数是0，第2个相同的数是6，…，若第n个相同的数是102，则n等于( )
A．18B．19C．20D．21
4．（2022·湖北房县·模拟预测）按一定规律排列的多项式： SKIPIF 1 < 0 ，…，根据上述规律，则第2022个多项式是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2020·河北滦州·模拟预测）古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”．从图7中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2021·江苏镇江·中考真题）如图，小明在3×3的方格纸上写了九个式子（其中的n是正整数），每行的三个式子的和自上而下分别记为A1，A2，A3，每列的三个式子的和自左至右分别记为B1，B2，B3，其中，值可以等于789的是（ ）
A．A1B．B1C．A2D．B3
7．（2021·湖北鹤峰·模拟预测）观察下列一组数的排列规律： SKIPIF 1 < 0 那么这一组数的第2021个数
__．
8．（2021·山东费县·二模）在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数---“好数”．定义：对于三位自然数n，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数为“好数”，如426是“好数”，因为4，2，6都不为0，且4+2=6，6能被6整除；643不是“好数”，因为6+4=10，10不能被3整除，问百位数字比十位数字大5的所有“好数”有__________个．
9．（2021·安徽·二模）观察下列各个等式：
第1个等式： SKIPIF 1 < 0 ÷ SKIPIF 1 < 0 －0=1；
第2个等式： SKIPIF 1 < 0 ÷ SKIPIF 1 < 0 －1= SKIPIF 1 < 0 ；
第3个等式： SKIPIF 1 < 0 ÷ SKIPIF 1 < 0 －2= SKIPIF 1 < 0 ；
……
请用上述等式反映出的规律解决下列问题：
（1）直接写出第5个等式；
（2）写出你猜想的第n个等式（用含n的代数式表示），并证明你的猜想．
10．（2021·重庆市永川区教育科学研究所一模）如果一个正整数能表示为两个正整数的平方差，那么称这个正整数为“智慧数”，否则称这个正整数为“非智慧数”．例如： SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ；，等等．因此3，5，8，，都是“智慧数”；而1，2，4，，都是“非智慧数”．对于“智慧数”，有如下结论：
①设 SKIPIF 1 < 0 为正整数（ SKIPIF 1 < 0 ），则 SKIPIF 1 < 0 ．∴除1以外，所有的奇数都是“智慧数”；
②设 SKIPIF 1 < 0 为正整数（ SKIPIF 1 < 0 ），则 SKIPIF 1 < 0 = ．∴ 都是“智慧数”．
(1)补全结论②中的空缺部分；并求出所有大于5而小于20的“非智慧数”；
(2)求出从1开始的正整数中从小到大排列的第103个“智慧数”．
11．（2021·山东禹城·二模）阅读下面的材料：按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．排在第一位的数称为第一项，记为 SKIPIF 1 < 0 ，排在第二位的数称为第二项，记为 SKIPIF 1 < 0 ，依次类推，排在第n位的数称为第n项，记为 SKIPIF 1 < 0 ．所以，数列的一般形式可以写成： SKIPIF 1 < 0 ．
一般地，如果一个数列从第二项起，每一项与它前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫做等差数列的公差，公差通常用d表示．如：数列1，3，5，7，…为等差数列，其中 SKIPIF 1 < 0 ，公差为 SKIPIF 1 < 0 ．
根据以上材料，解答下列问题：
（1）等差数列5，10，15，…的公差d为__________，第5项是__________．
（2）如果一个数列 SKIPIF 1 < 0 ，是等差数列，且公差为d，那么根据定义可得到：
SKIPIF 1 < 0 ．
所以
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
……
由此，请你填空完成等差数列的通项公式： SKIPIF 1 < 0 ．
（3） SKIPIF 1 < 0 是不是等差数列 SKIPIF 1 < 0 的项？如果是，是第几项？
（4）如果一个数列 SKIPIF 1 < 0 是等差数列，且公差为d，前n项的和记为 SKIPIF 1 < 0 ，请用含 SKIPIF 1 < 0 ，n，d的代数式表示 SKIPIF 1 < 0 ， SKIPIF 1 < 0 _________．
三、与代数计算有关的规律探究题
例题3 （2021·山东·利津县第一实验学校一模）探索发现：
SKIPIF 1 < 0 ＝1－ SKIPIF 1 < 0
SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 － SKIPIF 1 < 0
SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 － SKIPIF 1 < 0
根据你发现的规律，回答下列问题：
（1） SKIPIF 1 < 0 ＝__________； SKIPIF 1 < 0 ＝__________；
（2）利用发现的规律计算：
SKIPIF 1 < 0 ＋ SKIPIF 1 < 0 ＋ SKIPIF 1 < 0 ＋···＋ SKIPIF 1 < 0
（3）利用以上规律解方程：
SKIPIF 1 < 0 ＋ SKIPIF 1 < 0 ＋···＋ SKIPIF 1 < 0 ＝ SKIPIF 1 < 0
练习题
1．（2021·湖北鄂州·中考真题）已知 SKIPIF 1 < 0 为实数﹐规定运算： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，……， SKIPIF 1 < 0 ．按上述方法计算：当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 的值等于（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2021·浙江余杭·一模）a是不为2的有理数，我们把 SKIPIF 1 < 0 称为a的“哈利数”．如：3的“哈利数”是 SKIPIF 1 < 0 ＝﹣2，﹣2的“哈利数”是 SKIPIF 1 < 0 ，已知a1＝3，a2是a1的“哈利数”，a3是a2的“哈利数”，a4是a3的“哈利数”，…，依此类推，则a2019＝（ ）
A．3B．﹣2C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2020·广西贺州·中考真题）我国宋代数学家杨辉发现了 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ，1，2，3，…）展开式系数的规律：
以上系数三角表称为“杨辉三角”，根据上述规律， SKIPIF 1 < 0 展开式的系数和是（ ）
A．64B．128C．256D．612
4．（2021·山东阳谷·一模）我国南宋数学家杨辉用“三角形”解释二项和的乘方规律，称之为“杨辉三角”，这个“三角形”给出了 SKIPIF 1 < 0 的展开式的系数规律（按 SKIPIF 1 < 0 的次数由大到小的顺序）
1 1 SKIPIF 1 < 0
1 2 1 SKIPIF 1 < 0
1 3 3 1 SKIPIF 1 < 0
1 4 6 4 1 SKIPIF 1 < 0
… …
请依据上述规律，写出 SKIPIF 1 < 0 展开式中含 SKIPIF 1 < 0 项的系数是（ ）
A．-2021B．2021C．4042D．-4042
5．（2021·湖北·华中科技大学附属中学一模）我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉（约13世纪）所著的《详解九章算术》一书中，用如图的三角形解释二项和 SKIPIF 1 < 0 的展开式的各项系数，此三角形称为“杨辉三角”．根据“杨辉三角”设 SKIPIF 1 < 0 的展开式中各项系数的和为 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2020·湖南邵东·三模）a是不为1的有理数，我们把 SKIPIF 1 < 0 称为a的差倒数，如2的差倒数为 SKIPIF 1 < 0 ，-1的差倒数为 SKIPIF 1 < 0 ，已知 SKIPIF 1 < 0 ＝5， SKIPIF 1 < 0 是 SKIPIF 1 < 0 差倒数， SKIPIF 1 < 0 是 SKIPIF 1 < 0 差倒数， SKIPIF 1 < 0 是 SKIPIF 1 < 0 差倒数，以此类推…， SKIPIF 1 < 0 的值是_____．
7．（2021·四川眉山·中考真题）观察下列等式： SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ；
……
根据以上规律，计算 SKIPIF 1 < 0 ______．
8．（2020·山东鱼台·一模）计算下列各式的值： SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ．观察所得结果，总结存在的规律，应用得到的规律可得 SKIPIF 1 < 0 =_____________．
9．（2021·河北新华·一模）嘉琪通过计算和化简下列两式，发现了一个结论，请你帮助嘉琪完成这一过程．
（1）计算： SKIPIF 1 < 0 ；
（2）化简： SKIPIF 1 < 0 ；
（3）请写出嘉琪发现的结论．
10．（2021·安徽包河·一模）观察下列等式：
第1个等式： SKIPIF 1 < 0 ；
第2个等式： SKIPIF 1 < 0 ；
第3个等式： SKIPIF 1 < 0 ；
第4个等式： SKIPIF 1 < 0 ；
…
根据你观察到的规律，解决下列问题：
（1）请写出第5个等式：_____________________；
（2）请写出第 SKIPIF 1 < 0 个等式：___________________________（用含 SKIPIF 1 < 0 的等式表示），并证明．
四、图形变换规律探究题
例题4（2020·河北·模拟预测）如图，正六边形 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴重合，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴的正半轴上，已知，正六边形的边长为1，沿 SKIPIF 1 < 0 轴向右无滑动滚动，当边 SKIPIF 1 < 0 落到 SKIPIF 1 < 0 轴上时，我们记为一次滚动完成，此时正六边形记为 SKIPIF 1 < 0 ，请回答：
（1）点 SKIPIF 1 < 0 的坐标为__________；
（2）当正六边形滚动2020次后，点 SKIPIF 1 < 0 运动过的轨迹长__________．
练习题
1．（2021·江苏·靖江外国语学校一模）如图，在直角坐标系中放置一个边长为 SKIPIF 1 < 0 的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A第三次回到x 轴上时，点A运动的路线与x轴围成的图形的面积和为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2021·全国·九年级专题练习）第一次：将点 SKIPIF 1 < 0 绕原点 SKIPIF 1 < 0 逆时针旋转 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ；
第二次：作点 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 轴的对称点 SKIPIF 1 < 0 ；
第三次：将点 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 逆时针旋转 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ；
第四次：作点 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 轴的对称点 SKIPIF 1 < 0 …，
按照这样的规律，点 SKIPIF 1 < 0 的坐标是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2020·山东宁津·一模）在平面直角坐标系中，点P（a,b）绕点O顺时针旋转45°为一次变换，第2020次变换后得点P′，则点P′的坐标为（ ）
A．（ a, b）B．（-a,-b）C．（b,-a）D．（b,-a）
4．（2022·山东陵城·九年级期末）如图，直线 SKIPIF 1 < 0 与x轴、y轴分别相交于点A、B，过点B作 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 绕点O顺时针旋转，每次旋转 SKIPIF 1 < 0 ，则第2021次旋转结束时，点C的对应点 SKIPIF 1 < 0 落在反比例函数 SKIPIF 1 < 0 的图象上，则k的值为（ ）
A． SKIPIF 1 < 0 B．4C． SKIPIF 1 < 0 D．6
5．（2021·全国·九年级专题练习）如图，在平面直角坐标系 SKIPIF 1 < 0 中，正方形 SKIPIF 1 < 0 的顶点坐标分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 绕点A旋转 SKIPIF 1 < 0 得点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 绕点B旋转 SKIPIF 1 < 0 得点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 绕点C旋转 SKIPIF 1 < 0 得点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 绕点D旋转 SKIPIF 1 < 0 得点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 绕点A旋转 SKIPIF 1 < 0 得点 SKIPIF 1 < 0 ，……，重复操作依次得到点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，……，则点 SKIPIF 1 < 0 的坐标为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2021·江苏·九年级专题练习）如图，将半径为2cm，圆心角为36°的扇形纸片AOB，在射线MN的方向上作无滑动的滚动至扇形A′O′B′处，则圆心O经过的路径长为_____cm．
7．（2021·河北·邯郸市第二十三中学九年级期中）如图1，将一个正三角形绕其中心最少旋转 SKIPIF 1 < 0 ，所得图形与原图的重叠部分是正六边形；如图2，将一个正方形绕其中心最少旋转 45°，所得图形与原图形的重叠部分是正八边形；依此规律，将一个正七边形绕其中心最少旋转______ SKIPIF 1 < 0 ，所得图形与原图的重叠部分是正多边形．在图2中，若正方形的边长为 SKIPIF 1 < 0 ，则所得正八边形的面积为_______．

8．如图，在直角坐标系中，已知点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ，将线段 SKIPIF 1 < 0 按逆时针方向旋转 SKIPIF 1 < 0 ，再将其长度伸长为 SKIPIF 1 < 0 的 SKIPIF 1 < 0 倍，得到线段 SKIPIF 1 < 0 ；又将线段 SKIPIF 1 < 0 按逆时针方向旋转 SKIPIF 1 < 0 ，长度伸长为 SKIPIF 1 < 0 的 SKIPIF 1 < 0 倍，得到线段 SKIPIF 1 < 0 ．．．．．．如此下去，得到线段 SKIPIF 1 < 0 为正整数)，则点 SKIPIF 1 < 0 的坐标为 __________________．
9．（2021·广东乳源·三模）在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°．若点A1的坐标为(3,0)，OA1=OC2，OA2=OC3，OA3=OC4，…则依此规律，点A2021的坐标为______．
10．（2020·黑龙江齐齐哈尔·中考真题）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，4 SKIPIF 1 < 0 ），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+12 SKIPIF 1 < 0 ，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是_____．
11．（2021·广西·南宁三中九年级阶段练习）如图Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝1，且AC在直线l上，将△ABC绕点A顺时针旋转到①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝2+ SKIPIF 1 < 0 ；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝3+ SKIPIF 1 < 0 ；…按此规律继续旋转，直到点P2020为止，则AP2020等于_______．
五、函数规律探究题
例题5（2021·山东·宁津县教育和体育局教育科学研究所二模）如图所示，在x轴的正半轴上依次截取OA1＝A1A2＝A2A3＝A3A4＝A4A5…，过A1、A2、A3、A4、A5…分别作x轴的垂线与反比例函数 SKIPIF 1 < 0 的图象交于点P1、P2、P3、P4、P5…，并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…，按此作法进行下去，则S2021的值为____．
练习题
1．（2021·山东莘县·三模）如图，直线l：y＝x+1交y轴于点A1，在x轴正方向上取点B1，使OB1＝OA1；过点B1，作A2B1⊥x轴，交l于点A2，在x轴正方向上取点B2，使B1B2＝B1A2；过点B2作A3B2⊥x轴，交l于点A3，在x轴正方向上取点B3使B2B3＝B2A3；…记△OA1B1面积为S1，△B1A2B2面积为S2，△B2A3B3面积为S3，…则S2021等于（ ）
A．24039B．24038C．24037D．24036
2．（2021·山东济南·中考真题）新定义：在平面直角坐标系中，对于点 SKIPIF 1 < 0 和点 SKIPIF 1 < 0 ，若满足 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ； SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则称点 SKIPIF 1 < 0 是点 SKIPIF 1 < 0 的限变点．例如：点 SKIPIF 1 < 0 的限变点是 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 的限变点是 SKIPIF 1 < 0 ．若点 SKIPIF 1 < 0 在二次函数 SKIPIF 1 < 0 的图象上，则当 SKIPIF 1 < 0 时，其限变点 SKIPIF 1 < 0 的纵坐标 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2021·江苏丰县·模拟预测）如图，在平面直角坐标系中，直线l：y＝ SKIPIF 1 < 0 x﹣ SKIPIF 1 < 0 与x轴交于点B1，以OB1为一边在OB1上方作等边△A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为一边在A1B2上方作等边△A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为一边在A2B3上方作等边△A3A2B3，…，则A2020的横坐标是_____．
4．（2021·广东潮南·一模）如图，直线 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴，与直线 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，以原点 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 长为半径画圆弧交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ；再作 SKIPIF 1 < 0 轴，交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，以原点 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 长为半径画圆弧交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ； SKIPIF 1 < 0 ，按此作法进行下去，则点 SKIPIF 1 < 0 的坐标为__．
5．（2021·全国·九年级课时练习）如图，在平面直角坐标系中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…和 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…分别在直线 SKIPIF 1 < 0 和x轴上． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，……都是等腰直角三角形，如果点 SKIPIF 1 < 0 ，那么b的值是________； SKIPIF 1 < 0 的纵坐标是________．
6．（2021·山东牡丹·三模）如图，在平面直角坐标系 SKIPIF 1 < 0 中，直线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 交y轴于点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…， SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…， SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴的正半轴上，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，…， SKIPIF 1 < 0 ，依次均为等腰直角三角形，点 SKIPIF 1 < 0 的坐标是______．
7．（2021·四川广安·中考真题）如图，在平面直角坐标系中， SKIPIF 1 < 0 轴，垂足为 SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 逆时针旋转到 SKIPIF 1 < 0 的位置，使点 SKIPIF 1 < 0 的对应点 SKIPIF 1 < 0 落在直线 SKIPIF 1 < 0 上，再将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 逆时针旋转到 SKIPIF 1 < 0 的位置，使点 SKIPIF 1 < 0 的对应点 SKIPIF 1 < 0 也落在直线 SKIPIF 1 < 0 上，以此进行下去……若点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ，则点 SKIPIF 1 < 0 的纵坐标为______．
8．（2021·江苏邳州·二模）如图，在平面直角坐标系中，直线 SKIPIF 1 < 0 为正比例函数 SKIPIF 1 < 0 的图像，点 SKIPIF 1 < 0 的坐标为(1，0)，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴的垂线交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，以 SKIPIF 1 < 0 为边作正方形 SKIPIF 1 < 0 ；过点 SKIPIF 1 < 0 作直线 SKIPIF 1 < 0 的垂线，垂足为 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，以 SKIPIF 1 < 0 为边作正方形 SKIPIF 1 < 0 ；过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴的垂线，垂足为 SKIPIF 1 < 0 ，交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，以 SKIPIF 1 < 0 为边作正方形 SKIPIF 1 < 0 ，…，按此规律操作下所得到的正方形 SKIPIF 1 < 0 的面积是______．
9．（2021·山东青岛·三模）如图，在平面直角坐标系xOy中，抛物线y=x(x-5)(0≤x≤5)的图象记作y1，它与x轴的交于点O，x1，将y1绕x1旋转180°得到y2，y2与x轴相交于点x1，x2，将y2绕点x2旋转180°得到y3，y3与x轴相交于x2，x3；…，按照这个规律在x轴上依次得到点x1，x2，x3，…，xn，以及抛物线y1，y2，y3，…，yn，则点x6的坐标为 ____；yn的顶点坐标为 _____(n为正整数，用含n的代数式表示)．
10．（2021·广东·佛山市三水区三水中学附属初中三模）如图，一段抛物线： SKIPIF 1 < 0 记为 SKIPIF 1 < 0 ，它与 SKIPIF 1 < 0 轴交于两点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 旋转 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 ；将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 旋转 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 如此进行下去，直至得到 SKIPIF 1 < 0 ，若点 SKIPIF 1 < 0 在第2021段抛物线上，则 SKIPIF 1 < 0 的值为 __．
11．（2021·全国·九年级课时练习）如图，平行于 SKIPIF 1 < 0 轴的直线 SKIPIF 1 < 0 分別交函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图象于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴的平行线交 SKIPIF 1 < 0 的图象于点 SKIPIF 1 < 0 ，直线DE SKIPIF 1 < 0 AC，交 SKIPIF 1 < 0 的图象于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _______．
12．（2022·福建·厦门五缘实验学校模拟预测）如图，直线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，与函数 SKIPIF 1 < 0 的图象分别交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ；与函数 SKIPIF 1 < 0 的图象分别交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 如果四边形 SKIPIF 1 < 0 的面积记为 SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 的面积记为 SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 的面积记为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，以此类推，则 SKIPIF 1 < 0 的值是______．
月份
1月份
2月份
3月份
4月份
5月份
6月份
7月份
…
12月份
兔子对数
1
1
2
3



…