中考数学二轮复习考点提分特训专题03 二次函数含参解析式问题（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点提分特训专题03 二次函数含参解析式问题（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点提分特训专题03二次函数含参解析式问题原卷版doc、中考数学二轮复习考点提分特训专题03二次函数含参解析式问题解析版doc等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
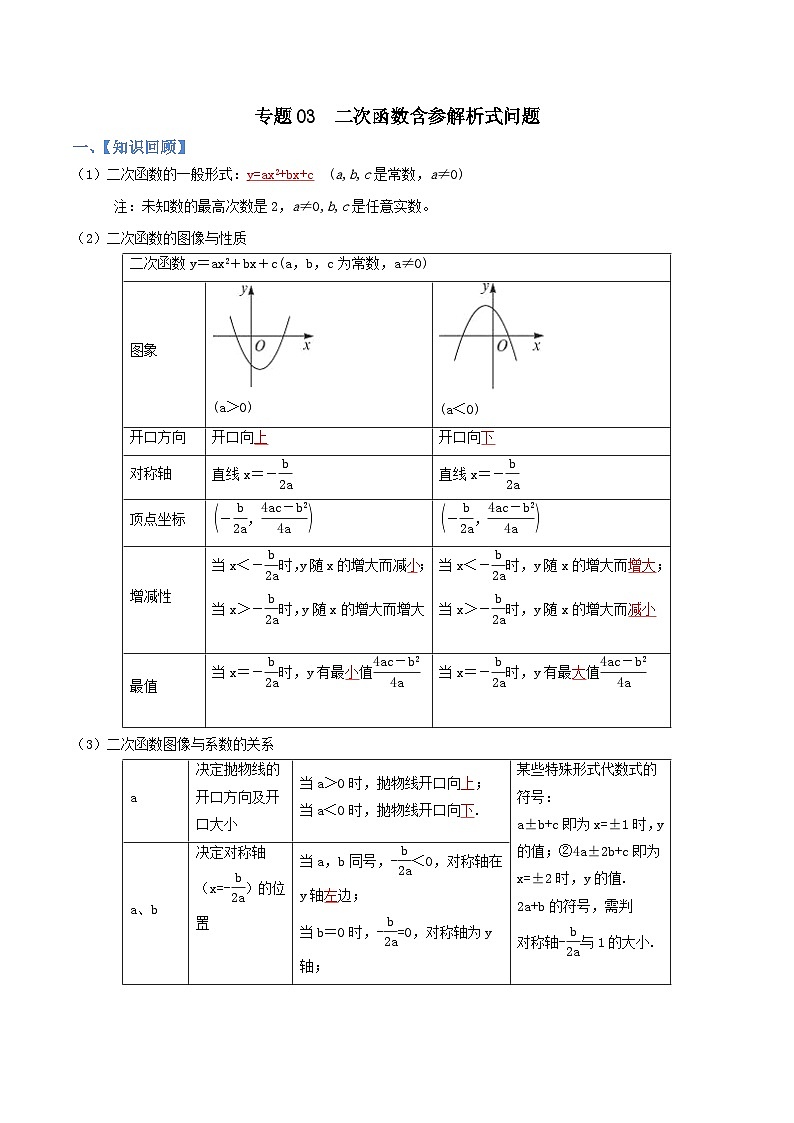
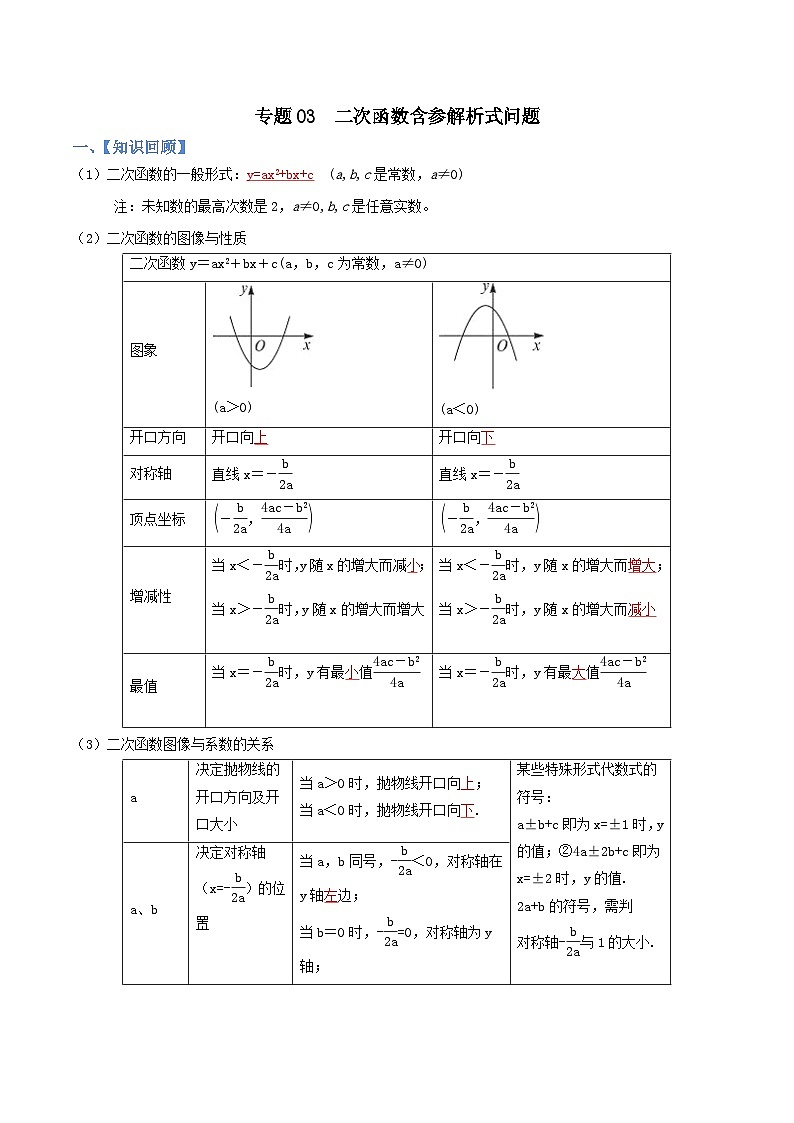
（1）二次函数的一般形式：y=ax2+bx+c (a,b,c是常数，a≠0)
注：未知数的最高次数是2，a≠0,b,c是任意实数。
（2）二次函数的图像与性质
（3）二次函数图像与系数的关系
（4）利用二次函数的对称轴判断函数值大小关系（福建常考选择题10）
方法技巧：
①已知点A（a，b）为二次函数图像上一点，对称轴已知x=c，则A点对称点B（2c-a，b）
②已知点A（a，c）、B（b，c）为二次函数图像上一点，则根据两点纵坐标相等，可知A、B为对称点，那么对称轴x= SKIPIF 1 < 0
③不等式解读： SKIPIF 1 < 0 →a到对称轴c的距离＞b到对称轴的距离
SKIPIF 1 < 0 →a到对称轴c的距离＝b到对称轴的距离
SKIPIF 1 < 0 →a到对称轴c的距离＜b到对称轴的距离
二、【考点类型】
考点1：二次函数函数图像与系数的关系
典例1：（2022·福建莆田·校考一模）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的图象如图所示，对称轴为直线x＝﹣1．有以下结论：①abc＞0；②a（k2+2）2+b（k2+2）＜a（k2+1）2+b（k2+1）（k为实数）；③m（am+b）≤﹣a（m为实数）；④c＜﹣3a；⑤ax2+bx+c+1＝0有两个不相等的实数根．其中正确的结论有 _____（只填写序号）．
【答案】①②③④⑤
【分析】根据抛物线开口方向，对称轴位置及抛物线与y轴交点位置判断①；根据函数的增减性可判断②；由抛物线开口方向及对称轴可得x＝﹣1时y最大，从而判断③；由对称轴可得b＝2a，由x＝﹣1时y＜0可判断④；根据函数y＝ax2+bx+c与y＝﹣1的图象有两个交点可判断⑤．
【详解】解：∵抛物线开口向下，与y轴交点在y轴正半轴，
∴a＜0，c＞0，
又∵对称轴是直线x＝﹣1，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴abc＞0，故①正确；
∵对称轴是直线x＝﹣1，抛物线开口向下，
∴当x＞﹣1时，y随x的增大而减小，
∵k是实数，
∴k2+2＞k2+1＞﹣1，
∴a（k2+2）2+b（k2+2）+c＜a（k2+1）2+b（k2+1）+c，
即a（k2+2）2+b（k2+2）＜a（k2+1）2+b（k2+1），故②正确；
∵抛物线开口向下，顶点坐标为（﹣1，a﹣b+c）
∴y最大＝a﹣b+c＝﹣a+c，
∴am2+bm+c≤﹣a+c，
即m（a+b）≤﹣a，
故③正确；
由图象知，x＝1时，y＜0，
∴a+b+c＜0，
∵b＝2a，
∴3a+c＜0，
∴c＜﹣3a，故④正确；
根据图象可知，函数y＝ax2+bx+c与y＝﹣1的图象有两个交点，
∴ax2+bx+c+1＝0有两个不相等的实数根，
故⑤正确，
故答案为：①②③④⑤．
【点睛】本题主要考查了二次函数图像的性质，解题的关键在于能够熟练掌握二次函数图像的性质．
【变式1】（2019秋·福建漳州·九年级统考期末）一次函数 SKIPIF 1 < 0 和反比例函数 SKIPIF 1 < 0 在同一个平面直角坐标系中的图象如图所示，则二次函数 SKIPIF 1 < 0 的图象可能是（ ）
A．B．
C．D．
【答案】A
【分析】根据反比例函数图象和一次函数图象经过的象限，即可得出 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，由此可以得出二次函数 SKIPIF 1 < 0 的图象开口向下，对称轴 SKIPIF 1 < 0 ，与 SKIPIF 1 < 0 轴的交点在 SKIPIF 1 < 0 轴的负半轴，再对照四个选项中的图象即可得出结论．
【详解】解：观察一次函数 SKIPIF 1 < 0 和反比例函数 SKIPIF 1 < 0 的图象可知： SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 二次函数 SKIPIF 1 < 0 的图象开口向下，对称轴 SKIPIF 1 < 0 ，与 SKIPIF 1 < 0 轴的交点在 SKIPIF 1 < 0 轴的负半轴，
故选：A．
【点睛】本题考查了反比例函数的图象、一次函数的图象以及二次函数的图象，根据反比例函数图象和一次函数图象经过的象限，找出 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 是解题的关键．
【变式2】（2021秋·福建福州·九年级福州华伦中学校考期末）已知点A（x1，y1）、B（x2，y2）在二次函数y＝x2＋bx＋c的图象上，当 SKIPIF 1 < 0 ＝1， SKIPIF 1 < 0 ＝3时， SKIPIF 1 < 0 ．若对于任意实数x1、x2都有 SKIPIF 1 < 0 ≥2，则c的范围是（ ）
A．c≥5B．c≥6C．c＜5或c＞6D．5＜c＜6
【答案】A
【分析】由当 SKIPIF 1 < 0 ＝1， SKIPIF 1 < 0 ＝3时，y1＝y2可得抛物线对称轴为直线x＝2，从而可得抛物线解析式，将函数解析式化为顶点式可得y1＋y2的最小值，进而求解．
【详解】∵当 SKIPIF 1 < 0 ＝1，x2＝3时， SKIPIF 1 < 0 ．
∴抛物线对称轴为直线x＝﹣ SKIPIF 1 < 0 ＝2，
∴b＝﹣4，
∴y＝ SKIPIF 1 < 0 ﹣4x＋c＝ SKIPIF 1 < 0 ＋c﹣4，
∴抛物线开口向上，顶点坐标为（2，c﹣4），
∴当y1＝y2＝c﹣4时，y1＋y2取最小值为2c﹣8，
∴2c﹣8≥2，
解得c≥5．
故选：A．
【点睛】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系，掌握二次函数与方程及不等式的关系．
【变式3】（2021·福建厦门·厦门双十中学思明分校校考二模）已知二次函数 SKIPIF 1 < 0 （其中x是自变量）的图象经过不同两点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且该二次函数的图象与x轴有公共点，则 SKIPIF 1 < 0 的值（ ）
A． SKIPIF 1 < 0 B．2C．3D．4
【答案】C
【分析】根据二次函数 SKIPIF 1 < 0 的图像经过 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，可得到二次函数的对称轴x= SKIPIF 1 < 0 ，又根据对称轴公式可得x=b，由此可得到b与c的数量关系，然后由该二次函数的图象与x轴有公共点列出不等式解答即可
【详解】解：∵二次函数 SKIPIF 1 < 0 的图像经过 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴对称轴x= SKIPIF 1 < 0 ，即x= SKIPIF 1 < 0 ，
∵对称轴x=b，
∴ SKIPIF 1 < 0 =b，化简得c=b-1，
∵该二次函数的图象与x轴有公共点，
∴△= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
∴b=2，c=1，
∴b+c=3，
故选：C．
【点睛】本题考查了二次函数图像的性质，包括图像上点的坐标特征、对称轴，利用抛物线与x轴交点的情况列出不等式，求得b，c的值．
考点2：利用二次函数的对称轴判断函数值的大小关系
典例2：（2021·贵州贵阳·统考一模）在平面直角坐标系中，点 SKIPIF 1 < 0 和 SKIPIF 1 < 0 在函数 SKIPIF 1 < 0 的图象上，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是___________．
【答案】0＜a＜1
【分析】先求出二次函数图像的对称轴方程和开口方向，再根据二次函数图像的对称性，列出不等式，进而即可求解．
【详解】解：∵函数 SKIPIF 1 < 0 的图象的对称轴为：直线 SKIPIF 1 < 0 ，开口向上，
又∵点 SKIPIF 1 < 0 和 SKIPIF 1 < 0 在函数 SKIPIF 1 < 0 的图象上，若 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，解得：0＜a＜1，
故答案是：0＜a＜1．
【点睛】本题主要考查二次函数图像和性质，掌握二次函数图像的轴对称性，是解题的关键．
【变式1】（2022·贵州毕节·统考二模）二次函数 SKIPIF 1 < 0 的图象过 SKIPIF 1 < 0 四个点，下列说法一定正确的是（ ）
A．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 B．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
C．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 D．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
【答案】C
【分析】求出抛物线的对称轴，根据抛物线的开口方向和增减性，根据横坐标的值，可判断出各点纵坐标值的大小关系，从而可以求解．
【详解】解： SKIPIF 1 < 0 二次函数 SKIPIF 1 < 0 的对称轴为：
SKIPIF 1 < 0 ，且开口向上，
SKIPIF 1 < 0 距离对称轴越近，函数值越小，
SKIPIF 1 < 0 ，
A，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 不一定成立，故选项错误，不符合题意；
B,若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 不一定成立，故选项错误，不符合题意；
C，若 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 一定成立，故选项正确，符合题意；
D，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 不一定成立，故选项错误，不符合题意；
故选：C．
【点睛】本题考查了二次函数的图象与性质及不等式，解题的关键是：根据二次函数的对称轴及开口方向，确定各点纵坐标值的大小关系，再进行分论讨论判断即可．
【变式2】13．（2022·福建福州·福建省福州教育学院附属中学校考模拟预测）已知抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴的交点为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是抛物线上不同于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的两个点，记 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，有下列结论：
①当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
②当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
③当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
④当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
其中正确结论的序号是（ ）
A．②③B．①③C．①②③④D．③
【答案】D
【分析】不妨假设 SKIPIF 1 < 0 ，利用图像法一一判断即可．
【详解】解：∵抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴的交点为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，
∴抛物线 SKIPIF 1 < 0 的对称轴为 SKIPIF 1 < 0 ，
不妨假设 SKIPIF 1 < 0 ．
①如图1中，当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故①错误；
②当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ，
这时点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在抛物线对称轴的左侧，
∵ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故②错误．
③∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴的上方，且 SKIPIF 1 < 0 离 SKIPIF 1 < 0 轴的距离比 SKIPIF 1 < 0 离 SKIPIF 1 < 0 轴的距离大，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故③正确．
④如图 SKIPIF 1 < 0 中，当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故④错误．
故选：D．
【点睛】本题考查抛物线与 SKIPIF 1 < 0 轴的交点，二次函数图像上的点的特征等知识．解题的关键是学会利用图像法解决问题．
【变式3】（2022·吉林长春·统考模拟预测）点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 均在抛物线 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ，a、b为常数）上，若 SKIPIF 1 < 0 ，则t的取值范围为________.
【答案】 SKIPIF 1 < 0
【分析】根据a＜0，可知抛物线开口向下，根据抛物线解析式可知抛物线的对称轴为x=1，当P、Q两点关于抛物线对称轴对称时，可求出t= SKIPIF 1 < 0 ，根据根据t+1＞t， SKIPIF 1 < 0 ，即可求出t的取值范围．
【详解】根据a＜0，可知抛物线开口向下，
根据抛物线解析式可知抛物线的对称轴为x=1，
则有 SKIPIF 1 < 0 时，y随x的增大而增大；
当P、Q两点关于抛物线对称轴对称时，则有 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，
∵t+1＞t， SKIPIF 1 < 0 ，
又∵则有 SKIPIF 1 < 0 时，y随x的增大而增大；
∴可知当P、Q在对称轴的左侧是肯定满足要求，P、Q均在对称轴的右侧时肯定不满足要求，
当P、Q分别在对称轴x=1的两侧时，
随着P、Q向x轴正向移动，P的纵坐标在逐渐增大，Q的纵坐标逐渐减小，
当P、Q两点关于抛物线对称轴对称时有 SKIPIF 1 < 0 ，
继续正方向移动，则有 SKIPIF 1 < 0 ，
∴满足 SKIPIF 1 < 0 的t的取值范围： SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0 ．
【点睛】本题考查了抛物线图像的性质，根据当P、Q两点关于抛物线对称轴对称时求出t的临界值是解答本题的关键．
巩固训练
一、单选题
1．（2023·辽宁鞍山·统考一模）已知点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 图象上的两点，且当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，则m的取值范围是（）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【分析】由当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，可得出 SKIPIF 1 < 0 ，解之即可得出m的取值范围．
【详解】解∶ SKIPIF 1 < 0 当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，
SKIPIF 1 < 0
SKIPIF 1 < 0
故选∶A．
【点睛】本题考查了二次函数的性质，根据当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 结合二次函数的性质，找出关于m的一元一次不等式是解题的关键．
2．（2022·广东·校联考模拟预测）已知抛物线 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 和 SKIPIF 1 < 0 两点，则n的值为（ ）
A．﹣2B．﹣4C．2D．4
【答案】B
【分析】根据 SKIPIF 1 < 0 和 SKIPIF 1 < 0 可以确定函数的对称轴 SKIPIF 1 < 0 ，再由对称轴的 SKIPIF 1 < 0 即可求解；
【详解】解：抛物线 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 和 SKIPIF 1 < 0 两点，
可知函数的对称轴 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
将点 SKIPIF 1 < 0 代入函数解析式，可得 SKIPIF 1 < 0 ；
故选B．
【点睛】本题考查二次函数图象上点的坐标；熟练掌握二次函数图象上点的对称性是解题的关键．
3.（2020·福建三明·统考二模）已知抛物线y=ax2+bx-2(a＞0)过A(-2，y1)，B(-3，y2)，C(1，y2)，D( SKIPIF 1 < 0 ，y3)四点，则y1，y2，y3的大小关系是( )
A．y1＞y2＞y3B．y2＞y1＞y3C．y1＞y3＞y2D．y3＞y2＞y1
【答案】D
【分析】由题意可知抛物线开口向上，对称轴为 SKIPIF 1 < 0 ，然后根据点A(-2、 SKIPIF 1 < 0 、B(-3， SKIPIF 1 < 0 、C(1， SKIPIF 1 < 0 、D( SKIPIF 1 < 0 ， SKIPIF 1 < 0 离对称轴的远近可判断 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 大小关系．
【详解】令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，即该抛物线与y轴的交点坐标是(0，-2)，
∵抛物线开口向上，对称轴为 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
故选：D．
【点睛】本题考查了二次函数图象上点的坐标特征，解题时，需熟悉抛物线的有关性质：抛物线的开口向上，则抛物线上的点离对称轴越远，对应的函数值就越大．
4．（2023·福建泉州·泉州五中校考三模）关于 SKIPIF 1 < 0 的一元二次方程 SKIPIF 1 < 0 有一个根是 SKIPIF 1 < 0 ，若二次函数 SKIPIF 1 < 0 的图象的顶点在第四象限，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【分析】由题意可知二次函数的图象过 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 由于顶点在第四象限，结合图象可判断 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即可求解．
【详解】∵关于 SKIPIF 1 < 0 的一元二次方程 SKIPIF 1 < 0 有一个根是 SKIPIF 1 < 0 ，
∴二次函数 SKIPIF 1 < 0 的图象过点 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
∵二次函数 SKIPIF 1 < 0 的图象的顶点在第四象限，并且图象过 SKIPIF 1 < 0 ，
∴该抛物线开口向上，对称轴在 SKIPIF 1 < 0 轴右侧
∴ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ．
故选D．
【点睛】本题考查了二次函数的图象与系数之间的关系，结合一元二次方程与二次函数图象之间的联系，综合判断系数的取值范围．熟练掌握一元二次方程与二次函数的图象及系数的关系是解本题的关键．
5．（2021·福建厦门·校考二模）小明在研究抛物线 SKIPIF 1 < 0 （h为常数）时，得到如下结论，其中正确的是（ ）
A．无论x取何实数，y的值都小于0
B．该抛物线的顶点始终在直线y＝x－1上
C．当－1＜x＜2时，y随x的增大而增大，则h＜2
D．该抛物线上有两点A（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），B（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），若 SKIPIF 1 < 0 ＜ SKIPIF 1 < 0 ， SKIPIF 1 < 0 + SKIPIF 1 < 0 ＞2h，则 SKIPIF 1 < 0 ＞ SKIPIF 1 < 0
【答案】D
【分析】根据二次函数的对称轴、二次函数图象上点的坐标特征、二次函数的性质判断即可．
【详解】解：A、∵ SKIPIF 1 < 0 ，－1